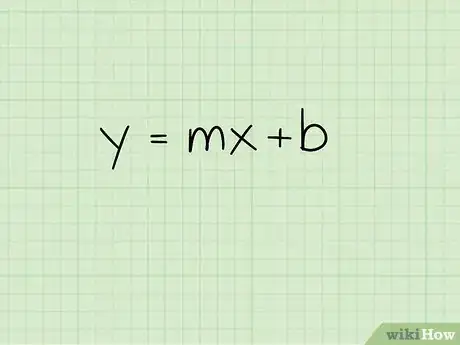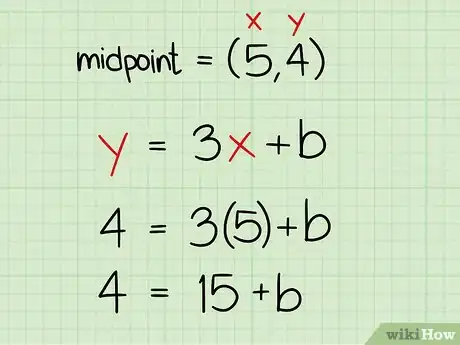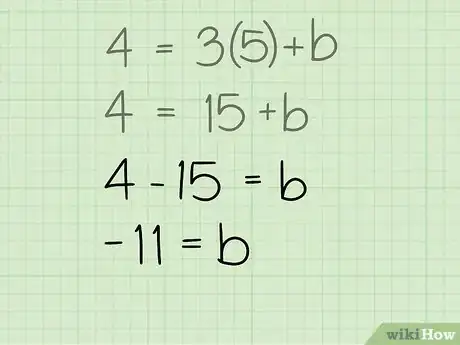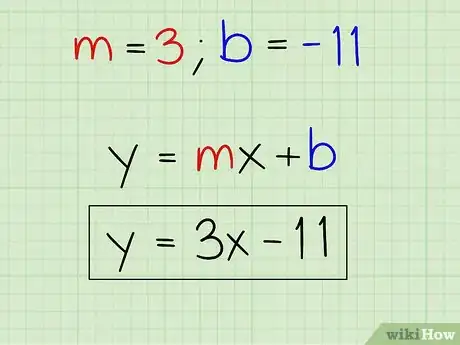Comment trouver l'équation de la médiatrice d'un segment

Informations concernant l'auteur.e

La médiatrice d'un segment de droite, délimité par deux points d'un plan, est une ligne qui coupe perpendiculairement (90°) le segment en deux parties égales. Pour trouver son équation, il vous faut trouver les coordonnées du milieu du segment, la pente entre ces deux points, puis l'opposée inverse de cette pente. Avec ces informations, vous aurez tout ce qui est nécessaire pour déterminer le coefficient directeur et la constante de l'équation de la médiatrice.

Méthode 1

Méthode 1 sur 2:
Préparer l'équation d'une médiatrice

1
Trouvez le milieu du segment de droite. Pour ce faire, il suffit de rentrer les coordonnées de ces deux points dans la formule suivante :
$({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}})$ $({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}})$ , ( $x_{1}$ $x_{1}$ , $y_{1}$ $y_{1}$ ) étant les coordonnées d'un des points et ( $x_{2}$ $x_{2}$ , $y_{2}$ $y_{2}$ ), les coordonnées de l'autre point. Prenons un exemple : soit un point A de coordonnées (2, 5) et un point B de coordonnées (8, 3). Voyez plutôt comment L'on procède pour trouver les coordonnées du milieu du segment (point $I$ $I$ ^{[1]
X
Source de recherche}) :
- $I\ \ ({\frac {2+8}{2}},{\frac {5+3}{2}})$
- $I\ \ ({\frac {10}{2}},{\frac {8}{2}})$
- $I\ \ (5,4)$
- Les coordonnées du milieu du segment AB sont (5, 4).
2
Trouvez la pente entre les deux points. Aussi appelée « coefficient directeur », cette pente $a$ $a$ s'obtient avec la formule suivante : $a={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ $a={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . La pente mesure, entre deux points, le rapport de la distance verticale sur la distance verticale. Reprenons le segment de droite précédent et calculons sa pente, les coordonnées respectives sont toujours (2, 5) et (8, 3)^{[2]
X
Source de recherche} :
- $a={\frac {3-5}{8-2}}$
- $a={\frac {-2}{6}}$
- $a=-{\frac {1}{3}}$ $a=-{\frac {1}{3}}$
  - La pente de la droite est de $-{\frac {1}{3}}$ . La fraction $a={\frac {-2}{6}}$ a été réduite à sa plus simple expression en divisant par 2.
3
Calculez ensuite l'opposée inverse de la pente. Une médiatrice est une droite qui coupe à angle droit un segment : sa pente est l'opposée inverse du segment. Pour calculer un tel nombre, il faut d'abord trouver l'inverse du nombre originel, puis en changer le signe. Vous pouvez aussi reprendre l'équation de la partie ci-dessus, mais en inversant les $x$ $x$ et les $y$ $y$ . Ainsi, l'opposée inverse de ${\frac {1}{2}}$ ${\frac {1}{2}}$ est
$-{\frac {2}{1}}(=-2)$ $-{\frac {2}{1}}(=-2)$ . Autre exemple : l'opposée inverse de - 4 est ${\frac {1}{4}}$ ${\frac {1}{4}}$ ^{[3]
X
Source de recherche}.
- Dans notre cas, la pente est de $-{\frac {1}{3}}$ , son opposée inverse est donc ${\frac {3}{1}}=3$ .
Publicité

Méthode 2

Méthode 2 sur 2:
Déterminer l'équation d'une médiatrice

1
Déterminez l'équation de la médiatrice. Comme c'est une droite affine, son équation se présente sous la forme : $y=mx+b$ . Dans cette équation, $m$ est la pente, $b$ est une constante (ordonnée à l'origine, la médiatrice croise l'axe des $x$ au point (0,b)), et enfin $x$ et $y$ sont les coordonnées d'un point de la médiatrice. Ceci étant posé, on peut trouver l'équation de notre médiatrice^{[4]
X
Source de recherche}.
2
Remplacez $m$ par l'opposée inverse de la pente du segment. On rappelle que l'opposée inverse de la pente entre les points A (2, 5) et B (8, 3) est 3. C'est cette valeur qui est la pente, le coefficient directeur de l'équation de la médiatrice, ici 3, d'où l'ébauche d'équation suivante :
- $y=mx+b$ , $m$ est à remplacer par 3 ;
- $y=3x+b$ .
3
Mettez en évidence $b$ . La moitié du travail est fait, il ne reste plus qu'à déterminer la constante $b$ $b$ . Pour cela, faites l'application numérique avec les coordonnées d'un point situé sur cette médiatrice. Ce point nous l'avons, puisque nous avons déterminé en début d'article le milieu du segment, c'était le point $I$ $I$ de coordonnées (5, 4). Ce point satisfait l'équation du segment, mais aussi celle de la médiatrice. Ce faisant, remplacez dans l'équation de la médiatrice $x$ $x$ et $y$ $y$ par respectivement 5 et 4.
- équation de départ : $y=3x+b$ ;
- application numérique avec $I$ : $4=3(5)+b$ ;
- $4=15+b$ .
4
Calculez la valeur de $b$ . Ce nombre est ce qu'on appelle la constante de l'équation, mais elle est aussi l'ordonnée du point d'intersection de la médiatrice et de l'axe des abscisses : pour $x=0$ $x=0$ , $y=b$ $y=b$ . Dans notre cas, nous avons isolé $b$ $b$ qu'il convient à présent de déterminer :
- $4=15+b$
- $4-15=15+b-15$
- $-11=b$
- $b=-11$
5
Présentez clairement l'équation de la médiatrice. Nous avons déterminé
$a$ $a$ (= 3) et $b$ $b$ (= - 11), nous pouvons donc présenter l'équation de la médiatrice. Elle est la suivante :
- $y=mx+b$ (équation formelle de départ)
- $y=3x-11$ (équation de la médiatrice)
- La médiatrice du segment de droite passant par les points A (2, 5) et B (8, 3) a pour équation : $y=3x-11$ . Vous pouvez vérifier que le milieu (5,4) satisfait bien l'équation : $4=3(5)-11$ . C'est parfait !
Publicité