Comment trouver l'inverse

Informations concernant l'auteur.e

Les inverses se rencontrent fréquemment dans les problèmes d'algèbre. Ainsi, quand vous divisez une fraction par une autre, il faut en fait multiplier la première par l'inverse de la seconde. Dans la résolution (graphique ou non) de fonctions, on a souvent besoin de calculer la fonction inverse.

Méthode 1

Méthode 1 sur 3:
Trouver l'inverse d'une fraction ou d'un entier

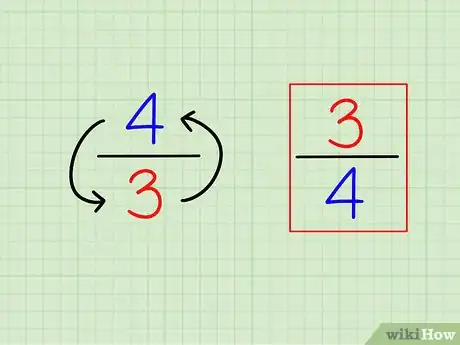
1
Trouvez l'inverse d'une fraction en la retournant. La notion d' « inverse » est relativement simple. L'inverse d'un nombre s'obtient en mettant ce nombre sur 1, en faisant donc "1 ÷ (nombre)". L'inverse d'une fraction est également une fraction. Il suffit « d'intervertir » le numérateur et le dénominateur, de la renverser en somme ^{[1]
X
Source de recherche} !
- Ainsi, l'inverse de ³/₄ est ⁴/₃.
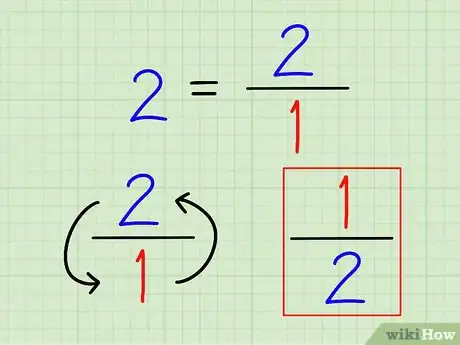
2
L'inverse d'un nombre entier est une fraction. L'inverse d'un nombre s'obtient en mettant ce nombre sur 1, en faisant donc "1 ÷ (nombre)". Vous le voyez, l'inverse d'un entier est une fraction qu'il faut laisser telle quelle. Il n'y a pas à faire de calcul pour obtenir un nombre décimal.
- Ainsi, l'inverse de 2 est : 1 ÷ 2 = ¹/₂.
Publicité

Méthode 2

Méthode 2 sur 3:
Trouver l'inverse d'un nombre mixte

1
Identifiez un nombre mixte. Un nombre mixte est composé d'une partie entière, suivie d'une fraction, par exemple 2 ⁴/₅. Vous aurez besoin de deux étapes pour trouver l'inverse d'une telle valeur.
2
Changez ce nombre en une fraction impropre. Nous vous rappelons d'une part que 1 peut toujours s'écrire sous forme de fraction : (nombre n)/(nombre n), et que, d'autre part, on ne peut additionner deux fractions que si elles ont été réduites au même dénominateur (valeur sous le trait de fraction). Partons du nombre 2 ⁴/₅. On peut le transformer ainsi :
- 2 ⁴/₅
- = 1 + 1 + ⁴/₅
- = ⁵/₅ + ⁵/₅ + ⁴/₅
- = ^{(5 + 5 + 4)}/₅
- = ¹⁴/₅ (fraction impropre).
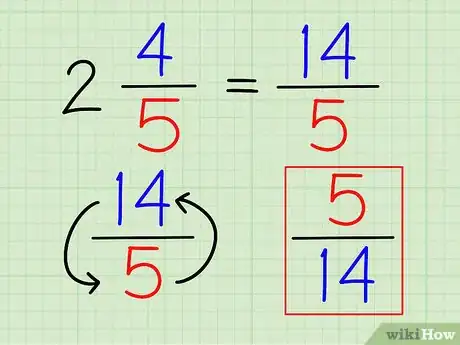
3
Retournez la fraction. Votre nombre mixte est désormais une fraction, et pour trouver l'inverse, il suffit de la retourner comme on l'a vu précédemment.
- Reprenons l'exemple précédent : l'inverse de ¹⁴/₅ est donc ⁵/₁₄.
Publicité

Méthode 3

Méthode 3 sur 3:
Trouver l'inverse d'un nombre décimal

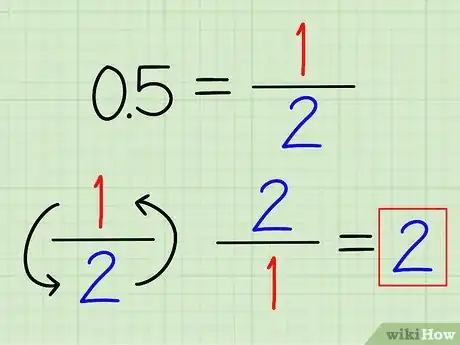
1
Essayez, si possible, de transformer ce nombre en fraction. Certains nombres décimaux (pas tous !) peuvent être convertis en fractions. Ainsi, 0,5 = ¹/₂ et 0,25 = ¹/₄. Comme cela a été vu, on trouve l'inverse de la fraction en la retournant.
- Ainsi, l'inverse de 0,5 est ²/₁ = 2.
2
Posez la division. Si votre nombre décimal ne peut être converti facilement en une fraction, le calcul de l'inverse est ramené à un simple problème de division : 1 ÷ (nombre décimal). Vous pouvez alors soit utiliser une calculatrice, soit faire le calcul à la main comme on va le voir.
- Par exemple, vous allez trouver l'inverse de 0,4 en faisant 1 ÷ 0,4.
3
Modifiez cette division en sorte de n'avoir que des nombres entiers. La première étape pour diviser des nombres décimaux consiste à déplacer la virgule vers la droite jusqu'à ce que tous les nombres soient des entiers. Attention ! Si vous déplacez la virgule d'un rang pour un des deux nombres, vous devez faire la même chose avec l'autre nombre. Ainsi, la division reste inchangée.
- Avec 1 ÷ 0,4, on obtient 10 ÷ 4. En dénominateur, on a multiplié par 10 pour faire disparaitre la virgule (0,4 x 10 = 4). En numérateur, on fait de même (1 x 10 = 10).
4
Faites alors l'opération. Utilisez la bonne vieille technique de la division pour trouver l'inverse. Ainsi, l'inverse de 0,4 est 10 ÷ 4, soit 2,5.

Publicité

Conseils

L'inverse négatif (ou « opposé inverse ») d'un nombre ressemble presque à l'inverse simple, on a simplement multiplié ce dernier par - 1. On lui a changé son signe, en somme ^{[2]
X
Source de recherche} ! Ainsi, l'opposé inverse de ³/₄ est - ⁴/₃.
L'inverse est également appelé « inverse multiplicatif ».
Le chiffre 1 est également son propre inverse, puisque 1 ÷ 1 = 1.
Par contre, l'inverse de 0 n'existe pas, car on ne peut pas diviser par 0 ^{[3]
X
Source de recherche}.