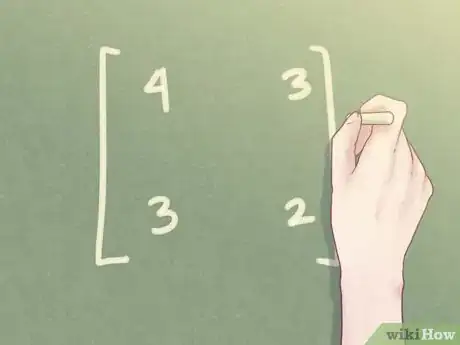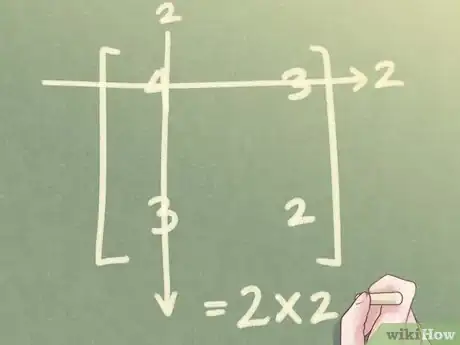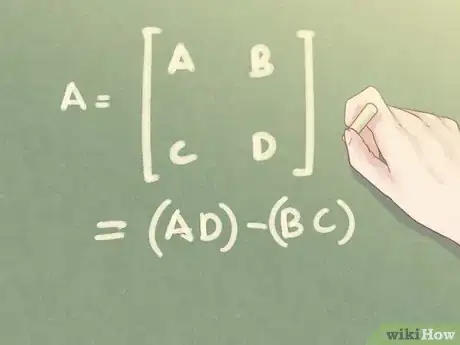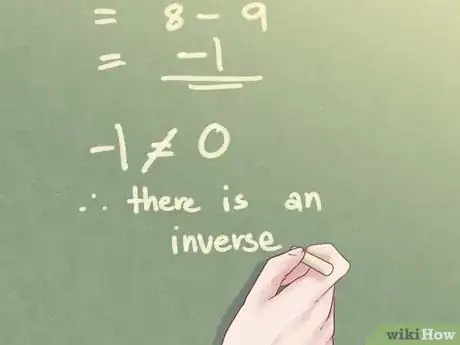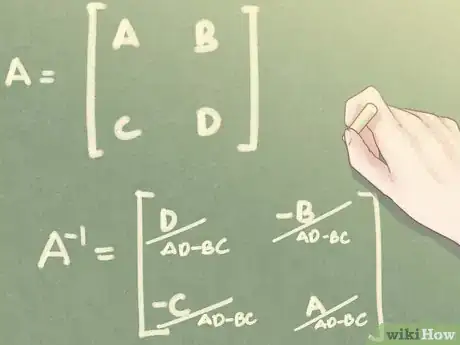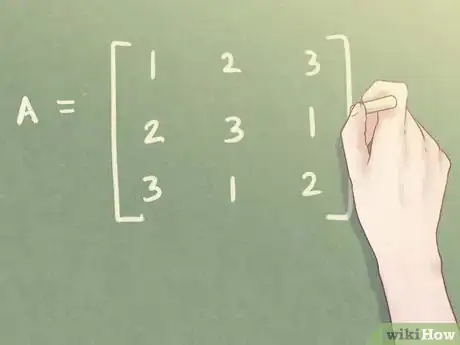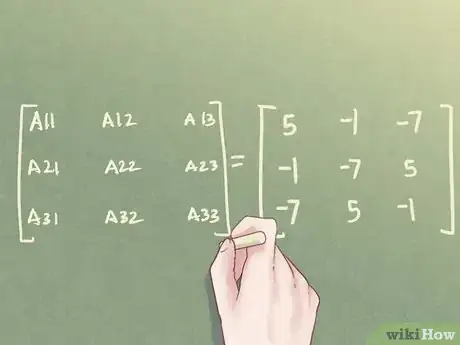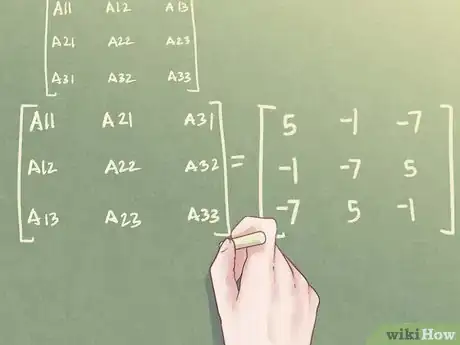Comment trouver l'inverse d'une matrice

Informations concernant l'auteur.e

Le calcul matriciel est une des branches de l'algèbre. Les matrices ont des usages importants dans la vie de tous les jours, en particulier en informatique. Sur le plan théorique, elles servent aussi beaucoup en mécanique quantique, mais aussi à résoudre des systèmes d'équations linéaires… Une matrice est en fait un tableau pratique de données avec des lignes et des colonnes, chaque donnée étant un coefficient. L'inverse d'une matrice est quelque peu similaire à l'inverse d'un nombre.

Méthode 1

Méthode 1 sur 2:
Trouver l'inverse d'une matrice carrée d'ordre 2

1
Vérifiez en premier lieu que la matrice est carrée. Pour trouver une matrice inverse, plusieurs conditions sont nécessaires, la première étant que la matrice de départ soit carrée, avec autant de lignes que de colonnes.
2
Vérifiez qu'elle est bien d'ordre 2. Si elle présente bien 2 lignes et 2 colonnes, elle est dite d'ordre 2 : passez à l'étape suivante. Si elle est carrée, mais d'un ordre supérieur (3, 4, 5, 6…), passez directement à la seconde méthode.
3
Calculez le déterminant de la matrice. C'est une des étapes fondamentales pour savoir si une matrice peut être inversée. Il est noté conventionnellement de deux façons : $|A|$ ou $det(A)$ . Si $A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ , alors $det(A)=ad-bc$ .
4
Intéressez-vous au déterminant. Si le déterminant est nul, il n'existe pas de matrice inverse et l'exercice s'arrête là. Dans tous les autres cas, il y a une matrice inverse.
5
Trouvez la transposée de la comatrice de $A$ . Il s'agit d'une matrice de même ordre que $A$ , notée $^{t}com(A)$ , dans laquelle les coefficients $a$ et $d$ ont été intervertis, et les coefficients $b$ et $c$ restent à leur place et voient leurs signes inversés. Dans notre exemple, $^{t}com(A)={\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}$ .
6
Apprenez la formule de la matrice inverse. Soit la matrice $A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ , l'inverse, notée $A^{-1}$ s'obtient grâce à la formule suivante :
$A^{-1}={\frac {1}{det(A)}}(^{t}com(A))={\frac {1}{ad-bc}}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}={\begin{pmatrix}{\frac {d}{ad-bc}}&{\frac {-b}{ad-bc}}\\{\frac {-c}{ad-bc}}&{\frac {a}{ad-bc}}\end{pmatrix}}$ .
7
Faites l'application numérique. Avec une matrice carrée d'ordre 2, l'inverse est facile à établir : vous intervertissez $a$ $a$ et $d$ $d$ , vous inversez les signes de $b$ $b$ et $c$ $c$ sans les changer de place, et vous divisez tous les coefficients obtenus par le déterminant.
- Avec la matrice $A={\begin{pmatrix}4&3\\3&2\end{pmatrix}}$ , le déterminant est :
  $det(A)=(4)(2)-(3)(3)=8-9=-1$ et la transposée de la matrice, $^{t}com(A)={\begin{pmatrix}2&-3\\-3&4\end{pmatrix}}$ . La matrice inverse est donc :
  $A^{-1}={\frac {1}{-1}}{\begin{pmatrix}2&-3\\-3&4\end{pmatrix}}=-1{\begin{pmatrix}2&-3\\-3&4\end{pmatrix}}={\begin{pmatrix}-2&3\\3&-4\end{pmatrix}}$ .
Publicité

Méthode 2

Méthode 2 sur 2:
Trouver l'inverse d'une matrice carrée d'ordre n

1
Vérifiez en premier lieu que la matrice est carrée. Pour trouver une matrice inverse, plusieurs conditions sont nécessaires, la première étant que la matrice de départ soit carrée, avec autant de lignes que de colonnes.
2
Vérifiez l'ordre de votre matrice carrée. Si votre matrice présente n lignes et n colonnes (avec n > 2), passez à l'étape suivante. Si elle est carrée et d’ordre 2, revenez à la première méthode.
- Prenons la matrice $A={\begin{pmatrix}1&2&3\\2&3&1\\3&1&2\end{pmatrix}}$ . Elle est carrée et d'ordre 3, car elle a trois lignes et trois colonnes.
3
Calculez tous les cofacteurs de la matrice. Le cofacteur, $A_{ij}$ $A_{{ij}}$ d'une matrice $A$ $A$ (i lignes et j colonnes) est défini par la formule : $A_{ij}=(-1)^{i+j}M_{ij}$ $A_{{ij}}=(-1)^{{i+j}}M_{{ij}}$ , $M_{ij}$ $M_{{ij}}$ étant le déterminant (ou le mineur) de la matrice obtenue en éliminant la i^e rangée et la j^e colonne de $A$ $A$ .
- Dans notre exemple, les cofacteurs sont les suivants :
  $A_{11}=5,A_{12}=-1,A_{13}=-7,A_{21}=-1,A_{22}=-7,A_{23}=5$
  $A_{31}=-7,A_{32}=5,A_{33}=-1$ .
4
Calculez le déterminant de la matrice. Il est noté conventionnellement $|A|$ $|A|$ ou $det(A)$ $det(A)$ . À partir d'une ligne ou d'une colonne (qui contient de préférence le plus de 0), faites une expansion des cofacteurs le long de cette dernière, soit la somme des produits des coefficients par leurs cofacteurs respectifs. La formule est la suivante : $det(A)=a_{i1}A_{i1}+a_{i2}A_{i2}+{\text{…}}+a_{in}A_{in}$ $det(A)=a_{{i1}}A_{{i1}}+a_{{i2}}A_{{i2}}+{\text{…}}+a_{{in}}A_{{in}}$ .
- Dans notre exemple, faites une expansion le long de la première ligne. Le déterminant se calcule ainsi : $det(A)=a_{11}A_{11}+a_{12}A_{12}+a_{13}A_{13}$ . Le calcul est le suivant : $det(A)=(1)(5)+(2)(-1)+(3)(-7)=-18$ .
5
Intéressez-vous à la valeur du déterminant. Si le déterminant est nul, il n'existe pas de matrice inverse. Dans tous les autres cas, la matrice inverse peut être établie.
- Dans notre exemple, le déterminant est non nul, puisqu'il est de -18.
6
Construisez la comatrice. C'est en fait une matrice qui contient dans le bon ordre tous les cofacteurs que vous avez précédemment calculés.
- Dans notre exemple, la comatrice ( $com(A)$ ) est la suivante :
  $com(A)={\begin{pmatrix}5&-1&-7\\-1&-7&5\\-7&5&-1\end{pmatrix}}$ .
7
Transposez les lignes et les colonnes de la comatrice. Comme pour la matrice carrée d'ordre 2, il faut établir la transposée de la comatrice en inversant les lignes et les colonnes.
- Dans notre exemple, la transposée de la comatrice est la suivante :
  $^{t}com(A)={\begin{pmatrix}5&-1&-7\\-1&-7&5\\-7&5&-1\end{pmatrix}}$ . Vous noterez que :
  $^{t}com(A)=com(A)$ , mais ce n'est pas toujours le cas.
8
Divisez la transposée de la comatrice par le déterminant. Vous devez multiplier chaque coefficient de la transposée de la comatrice par l'inverse du déterminant, ce qui revient à les diviser par ce même déterminant. Cela fait, vous obtenez votre matrice inverse.
- Avec notre cas concret, pour obtenir la matrice inverse, vous devez faire :
  $A^{-1}={\frac {1}{det(A)}}(^{t}com(A))={\frac {1}{-18}}{\begin{pmatrix}5&-1&-7\\-1&-7&5\\-7&5&-1\end{pmatrix}}$
  $A^{-1}={\begin{pmatrix}-{\frac {5}{18}}&{\frac {1}{18}}&{\frac {7}{18}}\\{\frac {1}{18}}&{\frac {7}{18}}&-{\frac {5}{18}}\\{\frac {7}{18}}&-{\frac {5}{18}}&{\frac {1}{18}}\end{pmatrix}}$
Publicité

Conseils

La matrice identité de rang n ( $I_{n}$ ) ne contient que des 0, sauf la diagonale principale (qui débute en haut et à gauche) qui ne contient que des 1.
N'oubliez jamais qu'une matrice (2,2) n'a d'inverse que si, et seulement si, son déterminant est non nul.
Si vous faites le produit de la matrice par son inverse ( $A\times A^{-1}$ ), vous obtenez la matrice identité ( $I_{n}$ ).