Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 7 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 24 425 fois.
En mathématiques, lors de l'étude d'une fonction, il est souvent demandé de tracer le graphe de cette fonction dans un repère composé de deux axes, l'un horizontal (axe des x ou des abscisses) et l'autre, vertical (axe des y ou des ordonnées). Il arrive fréquemment que le graphe coupe un de ses deux axes, sinon les deux. L’ordonnée du point d'intersection de la courbe avec l'axe des y s'appelle l'ordonnée à l'origine, tandis que l’abscisse du point d'intersection de la courbe avec l'axe des x est l'abscisse à l'origine. La détermination des coordonnées de ce point peut se faire visuellement ou par le calcul.
Étapes
Méthode 1
Méthode 1 sur 3:Déterminer graphiquement l'abscisse (fonction affine)
-
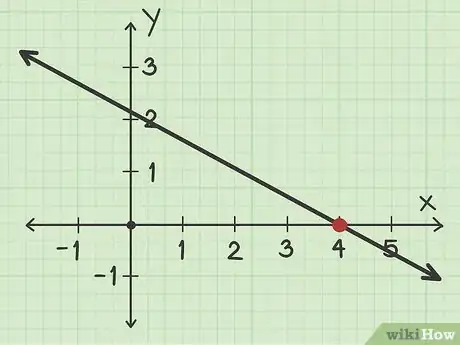
1Repérez l'axe des abscisses. Un repère dans le plan, orthonormé ou non, est constitué de deux axes : celui des abscisses (horizontal et gradué de gauche à droite) et celui des ordonnées (vertical et gradué de bas en haut [1] ). Trouvez sur l'axe des abscisses le point d'intersection de la droite avec cet axe : son abscisse est l'abscisse à l'origine.
-
2Déterminez le point d'intersection de la droite et de l'axe des abscisses. Une fois trouvé, vous le marquerez d'un gros point bien visible, éventuellement d'une autre couleur [2] . Si vous avez de la chance, la droite coupera votre axe sur une graduation, en 4 comme sur l'illustration. D'autres fois, le point peut être entre deux graduations, par exemple entre 4 et 5.
-
3Rédigez votre résultat. Il vous sera demandé d'indiquer clairement les coordonnées de ce point sous la forme [3] . La première coordonnée
() est donc l'abscisse à l'origine que vous avez lue (4) ou estimée (par exemple, 4,3), et correspond à la distance horizontale entre le 0 et le point d'intersection. Quant à la seconde coordonnée (), elle est dans ce cas-là de 0 [4] .- Si une droite coupe l'axe des abscisses en 4, alors les coordonnées du point d'intersection de la droite avec l'axe des abscisses sont .
Publicité
Méthode 2
Méthode 2 sur 3:Déterminer par le calcul l'abscisse (fonction affine)
-
1Voyez si vous avez affaire à une équation diophantienne. Une telle équation est en fait une équation polynomiale du type [5] . Sous cette forme, , , et sont des entiers, et et sont les coordonnées d'un point appartenant à la droite.
- Prenons comme exemple l'équation de la fonction suivante : .
-
2Remplacez par 0. Le point d'intersection avec l'axe des abscisses est le point du graphe qui coupe l'axe des abscisses [6] . Par définition, ce point a pour ordonnée 0 [7] . Vous devez donc poser afin de trouver la valeur de correspondante.
- Reprenons notre exemple et remplaçons par 0. L'équation se présente ainsi :
, soit après calcul et simplification .
- Reprenons notre exemple et remplaçons par 0. L'équation se présente ainsi :
-
3Calculez . Le calcul consiste à isoler à gauche, puis à faire disparaitre son coefficient en divisant des deux côtés par ce même coefficient. La valeur que vous allez trouver est l'abscisse à l'origine, soit celle du point d'intersection avec l'axe des abscisses.
- Prenons un exemple :
- Prenons un exemple :
-
4Présentez votre résultat. À la fin de votre travail, vous devez rédiger votre réponse. Vous indiquerez clairement que le point d'intersection de la droite et de l'axe des a pour coordonnées l'abscisse que vous avez trouvée, l'ordonnée, quant à elle, est égale par définition à 0. En conséquence, les coordonnées d'une abscisse à l'origine se présentent toutes sous la forme [8] .
- Pour la droite d'équation , le point d'intersection avec l'axe des abscisses a pour coordonnées .
Publicité
Méthode 3
Méthode 3 sur 3:Déterminer par le calcul l'abscisse (équation du second degré)
-
1Vérifiez que vous avez bien affaire à une équation du second degré. Une fonction du second degré a une équation qui peut se présenter sous sa forme développée : [9] . Cette équation a deux racines (ou solutions), une seule ou aucune ! Quand il y en a deux, le graphe est une parabole qui peut couper, et c'est le cas que nous envisagerons, à deux reprises l'axe des abscisses [10] .
- Prenons comme exemple la fonction . C'est bien une équation du second degré et celle-ci a deux racines, donc deux points d'intersection.
-
2Calculez les racines de l'équation. La formule générale est :
. Cette solution est double : et , avec le coefficient du terme au second degré (), le coefficient du terme au premier degré (), et la constante [11] . -
3Faites l'application numérique. La formule n'étant pas dans l'ordre des coefficients, soyez attentif(ve) au moment de remplacer les variables.
- Nous cherchons les abscisses des points d'intersection, nous posons donc :
. Appliqué à notre exemple, cela donne , et les solutions sont données par :
- Nous cherchons les abscisses des points d'intersection, nous posons donc :
-
4Simplifiez votre équation. Pour commencer, vous faites les produits (parenthèses) et soyez attentif aux signes (+ par - donne -).
- Reprenons notre exemple :
.
- Reprenons notre exemple :
-
5Calculez la puissance. Élevez au carré, puis opérez la somme de ce qui est en radicande (sous le signe de la racine).
- Reprenons notre exemple :
- Reprenons notre exemple :
-
6Calculez la première racine (). En fait, il n'y a pas d'ordre, vous pouvez calculer celle que vous voulez en premier, celle avec le signe + ou l'autre avec le signe -. Faites toutes les opérations et réduisez éventuellement le résultat à sa plus simple expression.
- Reprenons notre exemple :
- Reprenons notre exemple :
-
7Calculez la seconde racine (). Vous ferez attention à ne pas prendre la même formule que précédemment, mais bien celle dont le signe entre et
est l'opposé de la formule de la première racine. Calculez la racine, puis faites la somme en numérateur avant de diviser le tout par 2.- Reprenons notre exemple :
- Reprenons notre exemple :
-
8Présentez votre résultat. Il vous était demandé de presenter les coordonnées des points d'intersection de la parabole avec l'axe des abscisses. Les coordonnées d'un point se présentent sous la forme . Ici, vous aurez deux points ( et ). aura pour coordonnées et . L'ordonnée est toujours égale à 0, car tout point sur l'axe des à une ordonnée de 0 [12] .
- Pour la courbe (parabole) d'équation , les deux points d'intersection avec l'axe des abscisses ont pour coordonnées (à droite) et
(à gauche).
Publicité - Pour la courbe (parabole) d'équation , les deux points d'intersection avec l'axe des abscisses ont pour coordonnées (à droite) et
Conseils
- Une fonction affine a une équation de la forme , étant la pente (coefficient directeur) de la droite et l'ordonnée à l'origine. Pour trouver l'abscisse à l'origine, remplacez par 0, puis faites les calculs pour trouver la valeur de .
Références
- ↑ http://www.virtualnerd.com/pre-algebra/linear-functions-graphing/equations/x-y-intercepts/x-intercept-definition
- ↑ https://fr.khanacademy.org/math/algebra-home/alg-linear-eq-func/alg-x-and-y-intercepts/v/finding-x-intercept-of-a-line
- ↑ https://www.mathsisfun.com/definitions/ordered-pair.html
- ↑ http://www.virtualnerd.com/pre-algebra/linear-functions-graphing/equations/x-y-intercepts/x-intercept-definition
- ↑ http://courses.wccnet.edu/~palay/precalc/22mt01.htm
- ↑ https://fr.khanacademy.org/math/algebra-home/alg-linear-eq-func/alg-x-and-y-intercepts/v/finding-x-intercept-of-a-line
- ↑ http://www.virtualnerd.com/pre-algebra/linear-functions-graphing/equations/x-y-intercepts/x-intercept-definition
- ↑ http://www.virtualnerd.com/pre-algebra/linear-functions-graphing/equations/x-y-intercepts/x-intercept-definition
- ↑ http://mathworld.wolfram.com/QuadraticEquation.html






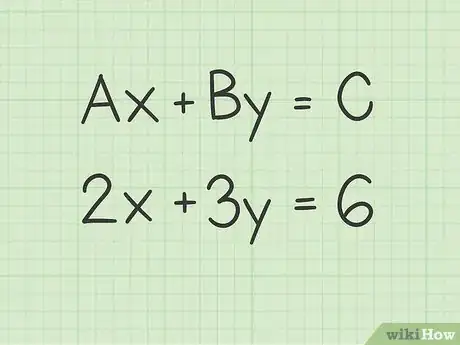





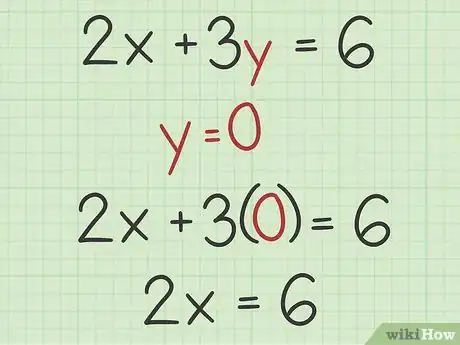



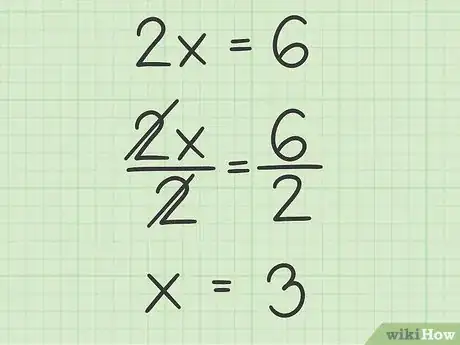





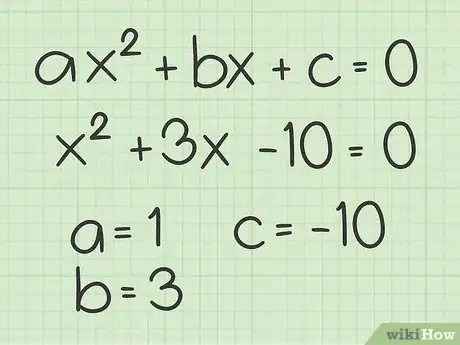


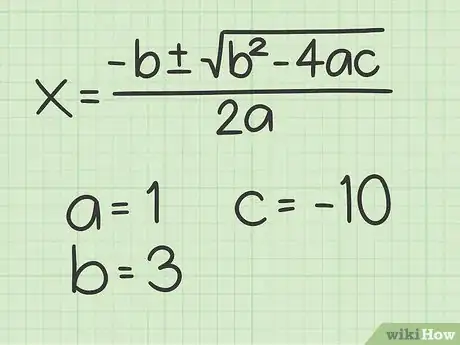




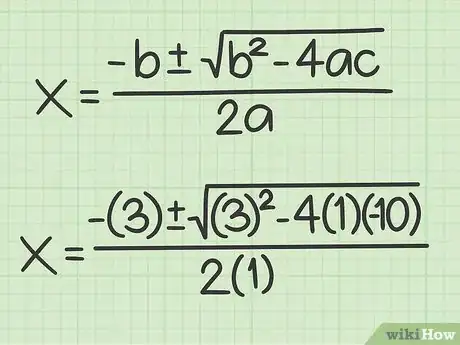



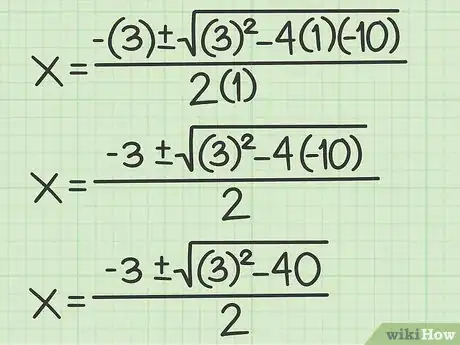


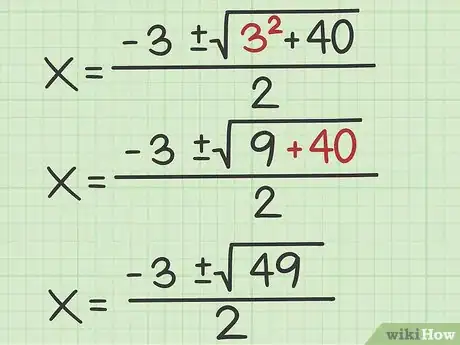


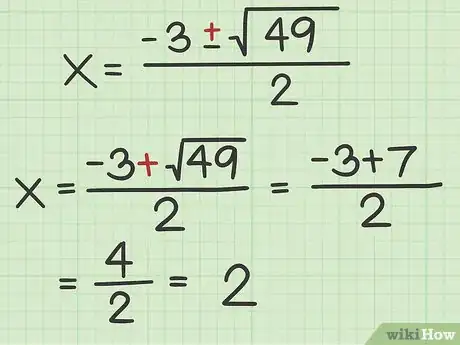





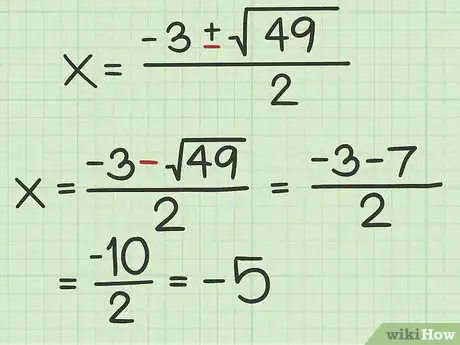


































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 24 425 fois.