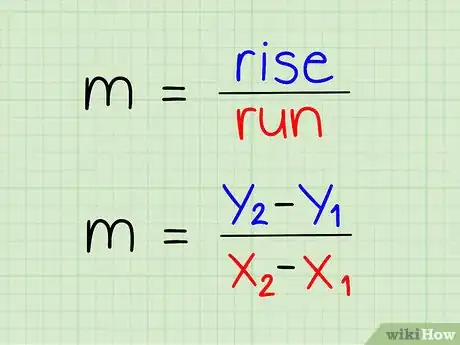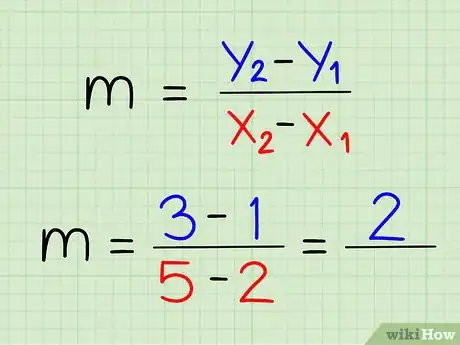Comment trouver la pente d'une droite

Informations concernant l'auteur.e

Les droites sont partout en mathématiques, que ce soit en algèbre ou en géométrie. Si vous savez comment trouver la pente d'une droite, beaucoup de concepts vous paraitront plus clairs, par exemple lorsqu'il s'agit de trouver si deux droites sont parallèles ou perpendiculaires, si elles possèdent une intersection, etc. Il est en fait très simple de trouver la pente d'une droite. Il suffit d'un peu de curiosité pour apprendre la démarche à suivre afin de calculer la pente d'une droite.

Partie 1

Partie 1 sur 2:
Découvrir la formule de la pente

1
Comprenez la formule de la pente.

Publicité

Partie 2

Partie 2 sur 2:
Calculer la pente

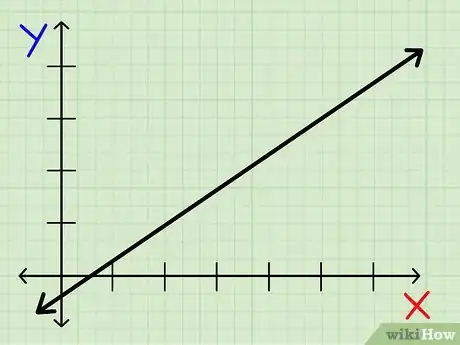
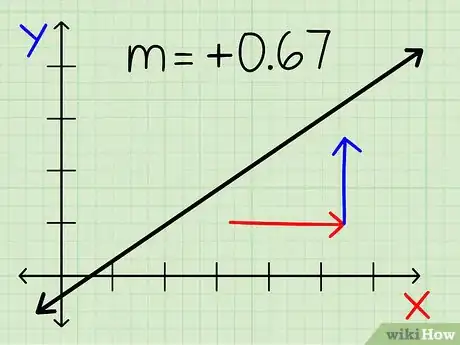
1
Tracez une droite dont vous voulez connaitre la pente. Assurez-vous que cette droite est linéaire, car dans le cas contraire vous ne pourrez pas en calculer la pente.
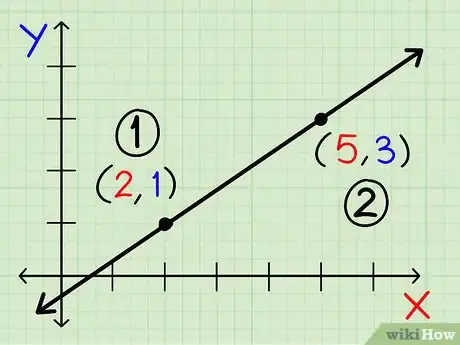
2
Choisissez les coordonnées de deux points par lesquels passe la droite. Les coordonnées sont les points x et y notés (x, y). Peu importe les points que vous choisissez, tant que vous prenez deux points différents sur une même droite.
3
Faites un autre choix. Déterminez le point dont les coordonnées seront « dominantes » dans votre équation. Peu importe quelles coordonnées vous choisissez, l'important est que celles-ci restent les mêmes tout au long de votre calcul. Les coordonnées dominantes ici seront notées x₁ et y₁. Les autres coordonnées seront notées x₂ et y₂.
4
Écrivez l'équation. Placez les coordonnées y au numérateur et les coordonnées x au dénominateur.
5
Soustrayez les coordonnées y.
6
Soustrayez les coordonnées x.
7
Continuez le calcul. Divisez le résultat de la soustraction des coordonnées y par celui de la soustraction des coordonnées x. Simplifiez le résultat si c'est possible.
8
Vérifiez si le résultat obtenu est logique.
- Les droites qui montent de la gauche vers la droite possèdent toujours une pente positive, même si la pente calculée est présentée sous forme de fraction.
- Les droites qui descendent de la gauche vers la droite possèdent toujours une pente négative, même si la pente calculée est présentée sous forme de fraction.
Publicité

Exemple

Soit une droite AB.
Coordonnées : A (-2 et 0) et B (0 et -2)
(y₂ - y₁) : -2 - 0 = -2 (Numérateur = -2)
(x₂ - x₁) : 0 - (-2) = 2 (Dénominateur = 2)
Pente de la droite AB = Numérateur/Dénominateur = -1

Conseils

Une fois que vous avez choisi les coordonnées du point dominant, ne vous trompez pas par la suite ou votre résultat sera faux.
Dans la formule de la droite y = ax + b, la pente de la droite correspond à la lettre « a », tandis que la lettre « y » correspond à la coordonnée y de n'importe quel point par lequel passe la droite, la lettre « x » correspond à la coordonnée x de n'importe quel point par lequel passe la droite et la lettre « b » correspond à l'ordonnée à l'origine de la droite.
Vous pouvez aussi trouver la réponse dans votre livre scolaire ou poser la question à votre professeur.

Avertissements

Ne confondez pas la formule de la pente avec les autres formules comme celle de la formule du calcul de distance entre deux points, la formule de l'équation d'une droite ou encore la formule des coordonnées d'un point milieu d'un segment.

Éléments nécessaires

Du papier millimétré (si possible)
Un plan affine ou une droite avec deux points donnés ainsi que leurs coordonnées
La formule de la pente
Un crayon, du papier, une règle, une calculatrice ou juste votre esprit
Une ou des droites
Des coordonnées x
Des coordonnées y