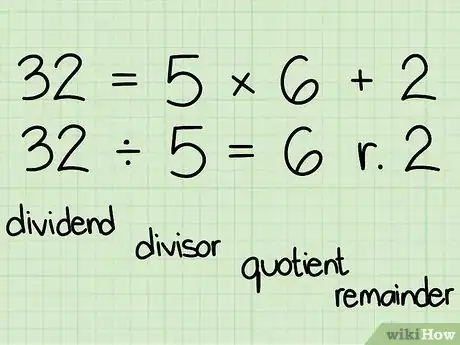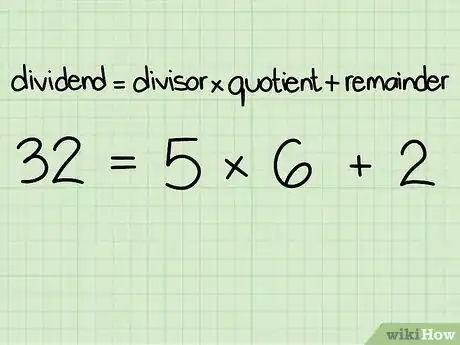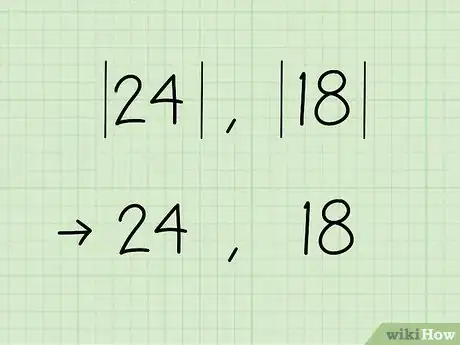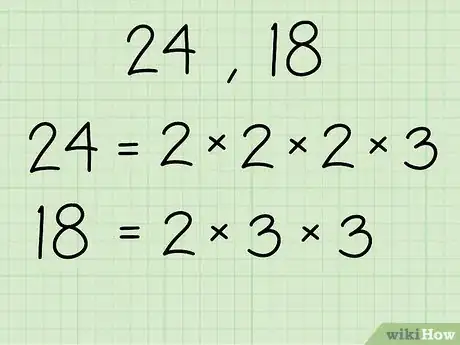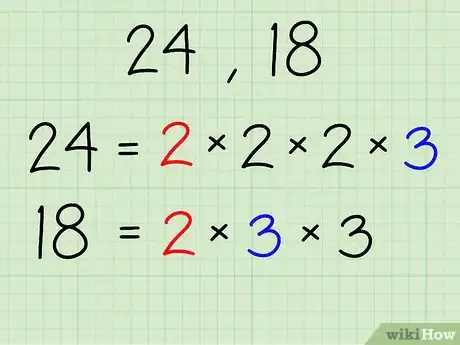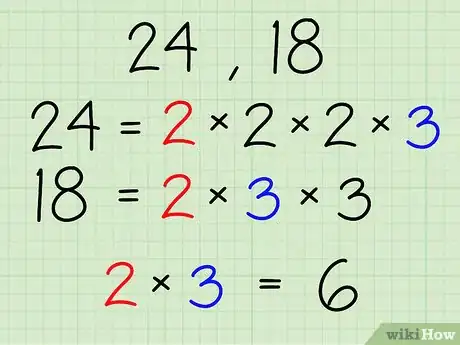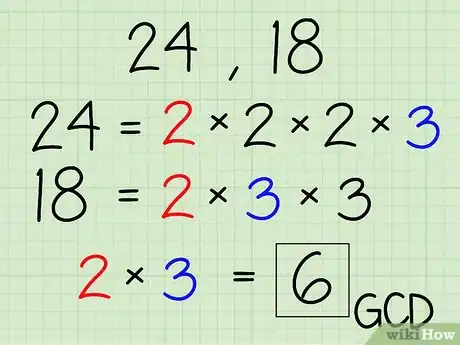Comment trouver le plus grand commun diviseur de deux entiers naturels

Informations concernant l'auteur.e

Le plus grand commun diviseur (PGCD) de deux nombres entiers est le plus grand entier qui divise en même temps ces deux entiers. Par exemple, le plus grand nombre qui divise à la fois 20 et 16 est 4 (16 et 20 ont, séparément, des diviseurs plus grands, mais pas un grand diviseur commun. Par exemple, 8 est un diviseur de 16, mais ce n'est pas un diviseur de 20.) À l'école primaire, la plupart des élèves apprennent la méthode de la "devinette" pour trouver le GCD. Par contre, il existe un moyen simple et rigoureux de trouver le PGCD. La méthode est appelée "algorithme d'Euclide". Pour nos explications, nous appellerons les deux nombres, a et b.

Méthode 1

Méthode 1 sur 2:
Utiliser l'algorithme

1
Enlevez tous les signes négatifs. Prenons les deux entiers : 32 et -5.
2
Quelques éléments de vocabulaire pour commencer ! Lorsque vous divisez 32 par 5 :
- - 32 est le dividende
  - 5 est le diviseur
  - 6 est le quotient
  - 2 est le reste (ou modulo)
3
Repérez le plus grand des deux nombres. Ce sera le dividende, et le plus petit sera le diviseur.
4
Écrivez l’algorithme suivant : dividende = diviseur x quotient + reste.
5
Placez le plus grand nombre comme dividende, et le plus petit comme diviseur.
6
Trouvez combien de fois le plus petit nombre est contenu dans le plus grand, et inscrivez-le dans l'algorithme comme quotient.
7
Calculez le reste, et inscrivez-le à l'endroit prévu dans l'algorithme.
8
Réécrivez l'algorithme, mais cette fois 1) utilisez l’ancien diviseur comme nouveau dividende et 2) utilisez le reste comme diviseur.
9
Répétez l'étape précédente jusqu'à ce que le reste soit égal à 0.
10
Le dernier diviseur est alors le plus grand commun diviseur (PGCD).
11
Passons à un exercice pratique : essayons de trouver le PGCD de 108 et 30 :
12
Remarquez où se positionnent le 30 et le 18 sur la première ligne pour pouvoir construire la deuxième ligne. Ensuite, comment on récupère 18 et 12 pour écrire la troisième ligne, et enfin comment on récupère le 12 et le 6 afin de créer la quatrième ligne. Les 3, 1, 1 et 2 qui suivent le symbole de multiplication ne servent pas. Ils indiquent le nombre de fois où le diviseur est contenu dans le dividende, de sorte qu'ils sont uniques à chaque ligne.

Publicité

Méthode 2

Méthode 2 sur 2:
Utiliser les facteurs premiers

1
Enlevez tous les signes négatifs.
2
Faites la décomposition en facteurs premiers de chaque entier et écrivez-les comme indiqué ci-dessous :
- Si on prend 24 et 18 comme exemples :
  - 24- 2 x 2 x 2 x 3
  - 18- 2 x 3 x 3
- Si on prend 50 et 35 comme exemples :
  - 50- 2 x 5 x 5
  - 35- 5 x 7
3
Identifiez tous les facteurs premiers communs :
- Si on reprend 24 et 18 comme exemples :
  - 24- 2 x 2 x 2 x 3
  - 18- 2 x 3 x 3
- Si on reprend 50 et 35 comme exemples :
  - 50- 2 x 5 x 5
  - 35- 5 x 7
4
Multipliez les facteurs communs.
- Dans le cas avec 24 et 18, il faut multiplier 2 par 3 pour obtenir 6. Six (6) est donc le plus grand facteur commun de 24 et de 18.
- Dans le cas avec 50 et 35, il n'y a rien à multiplier, puisque5 est le seul facteur commun, et donc le plus grand.
5
Voilà ! c’est fini !

Publicité

Conseils

On peut utiliser une autre notation : <dividende> mod <diviseur> = reste. Le PGCD (a, b) = b si mod b = 0 ; sinon, PGCD (a, b) = PGCD (b, a mod b).
Cette technique est très pratique lorsqu’il s’agit de réduire une fraction. Par l'exemple, la fraction -77/91 peut être simplifiée sous la forme : -11/13, parce que 7 est le plus grand commun diviseur de 77 et de 91.
Si 'a' ou 'b' sont nuls, la méthode ne peut fonctionner. Elle ne s’applique qu’avec des entiers non nuls. Les mathématiciens disent simplement que le plus grand commun diviseur de 0 et 0 est 0.
Pour nous résumer, cherchons le PGCD (-77, 91). Tout d'abord, utilisez 77 et non -77, donc PGCD (-77, 91) devient PGCD (77, 91). Puis, 77 étant inférieur à 91, donc on doit les inverser. De toute façon, l'algorithme vous montre rapidement l’infaisabilité de la chose.
Lorsque nous calculons 77 mod 91, nous obtenons 77 (avec 77 = 91 x 0 + 77). Inversé, cela nous donne : PGCD (77, 91) = PGCD (91, 77). 91 mod 77 donne 14 (14 est le reste). On n’a pas zéro, donc PGCD (91, 77) devient PGCD (77, 14). 77 mod 14 donne 7 qui n'est pas nul, donc PGCD (77, 14) devient PGCD (14, 7). 14 mod 7 est nul, puisque 14 = 7 x 2 n’a pas de reste. Au final, PGCD (-77, 91) = 7.