Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 9 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 94 901 fois.
Un multiple d'un nombre naturel est le produit de ce nombre entier et de n'importe quel autre entier naturel. Le plus petit commun multiple (PPCM) de deux (ou plusieurs) nombres entiers naturels non nuls est le plus petit entier qui soit à la fois multiple de ces deux nombres. Il existe plusieurs méthodes pour trouver un PPCM, nous en verrons quatre, mais dans tous les cas, il faut de toute façon décomposer les nombres de départ en facteurs premiers. Ces méthodes ne se limitent pas à la recherche du PPCM de deux nombres, elles servent aussi quand il y en a trois, quatre ou plus.
Étapes
Méthode 1
Méthode 1 sur 4:Trouver tous les multiples
-
1Observez vos nombres de départ. Cette méthode convient parfaitement lorsque vous devez trouver le PPCM de deux chiffres. Pour de grands nombres, il vaut mieux utiliser une autre méthode.
- Admettons qu'on vous demande de calculer le plus petit commun multiple de 5 et de 8. Vous le voyez, ce sont des chiffres : la méthode que nous allons utiliser est donc parfaite.
-
2Inscrivez divers multiples consécutifs du premier nombre. Le multiple d'un nombre est le produit de ce nombre et d'un entier [1] . Ainsi, tous les résultats d'une table de multiplication sont des multiples du nombre.
- C'est ainsi que 5, 10, 15, 20, 25, 30, 35, 40… sont tous des multiples de 5.
-
3Inscrivez divers multiples consécutifs du second nombre. Cette seconde série sera mise, par exemple, sous la première série de multiples afin de pouvoir comparer facilement.
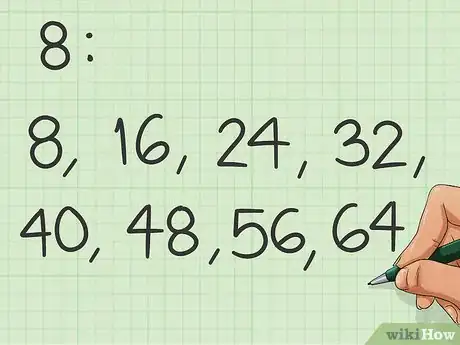
- C'est ainsi que les premiers multiples de 8 sont 8, 16, 24, 32, 40, 48, 56, 64…
-
4Trouvez le plus petit multiple commun. Comparez les deux listes et trouvez le plus petit nombre commun aux deux listes. Si, avec une liste de quatre ou cinq multiples, vous ne trouvez pas le multiple, il faudra prolonger les deux listes jusqu'à le trouver. Le premier que vous trouvez est le plus petit commun multiple [2] .
- En conclusion, 40 est non seulement un multiple de 8 et un multiple de 5, mais c'est le plus petit de tous les multiples communs de 8 et de 5.
Publicité
Méthode 2
Méthode 2 sur 4:Décomposer en produits de facteurs premiers
-
1Observez vos nombres de départ. Cette méthode, un peu plus longue, convient parfaitement lorsque vous devez trouver le PPCM de deux nombres élevés. Pour les chiffres et les petits nombres, il vaut mieux utiliser la méthode précédente.
- Si l'on vous demandait de trouver le plus petit commun multiple de 20 et de 84, vous devriez utiliser la méthode suivante.
-
2Décomposez le premier nombre en produits de facteurs premiers. Un facteur premier est un nombre qui ne peut être divisé que par 1 et par lui-même. Décomposer un nombre en produits de facteurs premiers consiste à trouver tous les nombres premiers qui, multipliés entre eux, donnent le nombre de départ. Pour les trouver, vous pouvez faire un arbre de facteurs. Cela fait, regroupez tous ces facteurs dans une équation.
- Ainsi, et , les facteurs premiers de 20 sont donc 2, 2 et 5. La décomposition peut s'écrire comme suit :
-
3Décomposez le second nombre en produits de facteurs premiers. Procédez exactement de la même façon que pour le premier nombre. Trouvez tous les facteurs qui, multipliés entre eux, donnent votre nombre de référence.
- C'est ainsi que : , et , les facteurs premiers de 84 sont donc : 2, 7, 3 et 2. La décomposition dans l'ordre peut s'écrire comme suit :
-
4Recherchez les facteurs communs. Inscrivez ces facteurs sur une ligne spécifique et sous la forme d'un produit. Chaque fois, vous barrerez le facteur commun dans chaque décomposition.
- Ainsi, 2 est un facteur commun une première fois, inscrivez quelque part en dessous de vos deux décompositions « », tout en barrant les deux 2, un dans chaque décomposition.
- À nouveau, 2 est un facteur commun, complétez la ligne commencée en mettant « » et barrez à nouveau les deux 2, un dans chaque décomposition.
-
5Complétez la ligne de calcul commencée. Toujours sous forme de produit, ajoutez tous les facteurs qui n'ont pas été rayés qui ne sont donc pas communs aux deux décompositions [3] .
- Dans notre exemple, , il ne reste plus que le 5, les deux 2 ayant été précédemment comptabilisés et barrés. Ce 5 sera mis à la suite du produit commencé, précédé d'un signe de multiplication :
- De même, nous avions : , et vous avez barré les deux 2, ce qui fait qu'il ne reste plus que le 7 et le 3, que vous ajouterez donc à la suite du produit commencé :
-
6Calculez le plus petit commun multiple. Voilà ! C'est presque fini : il ne vous reste plus qu'à faire le produit.
- Ainsi, . En conséquence, le plus petit commun multiple de 20 et 84 est 420.
Publicité
Méthode 3
Méthode 3 sur 4:Utiliser la méthode de la grille de facteurs communs
-
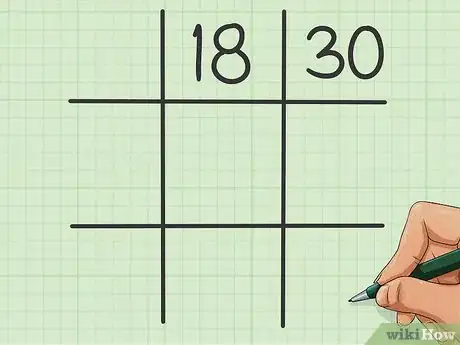
1Tracez une sorte de grille de morpion. Tracez trois traits parallèles verticaux et trois traits parallèles horizontaux, les verticaux étant perpendiculaires aux horizontaux. Vous avez ainsi trois lignes, trois colonnes et neuf cases. Vous devez obtenir quelque chose qui ressemble au symbole du dièse. Le premier nombre sera inscrit dans la case centrale de la ligne du haut, tandis que le second le sera dans celle juste à droite [4] .
- Si l'on vous a demandé de trouver le plus petit commun multiple de 18 et de 30, inscrivez 18 dans la case centrale de la ligne du haut et 30 dans celle située sur la même ligne, mais à droite.
-
2Trouvez un facteur commun à ces deux nombres. Inscrivez-le toujours sur la même ligne, mais dans la case vide de gauche. Vous pouvez prendre un facteur premier, mais ce n'est pas obligatoire.
- C'est ainsi que, 18 et 30 étant des nombres pairs, vous savez d'ores et déjà qu'ils ont en commun le facteur 2. Inscrivez 2 dans la case de gauche. Votre ligne est complète.
-
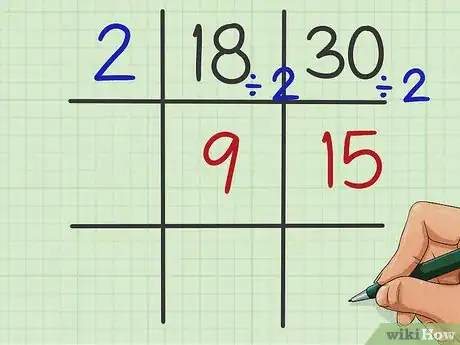
3Divisez chacun de vos nombres par le facteur choisi. Sous chacun des deux nombres de droite, inscrivez le quotient (résultat de la division) de chacune de ces divisions.
- Comme , inscrivez dans votre grille 9 sous le 18.
- Comme , inscrivez dans votre grille 15 sous le 30.
-
4Trouvez un facteur commun à ces deux quotients. S'il n'y en a pas, passez sans tarder à l'étape suivante. S'il y en a un, n'importe lequel, inscrivez-le dans la case de gauche de la ligne du milieu.
- Dans notre exemple, 9 et 15 sont tous divisibles par 3, c'est un facteur commun que vous allez inscrire dans la case de gauche de la ligne du milieu.
-
5Divisez chacun de vos quotients par le facteur choisi. Comme précédemment, inscrivez sous les quotients correspondants le quotient de leur division par le facteur choisi.
- Comme , inscrivez dans votre grille 3 sous le 9.
- Comme , inscrivez dans votre grille 5 sous le15.
-
6Si besoin était, agrandissez votre grille. Vous l'aurez compris, continuez ainsi jusqu'à ce que vos deux derniers quotients n'aient plus de facteur commun.
-
7Choisissez les bons nombres. Encerclez tous les valeurs qui se situent dans la colonne de gauche et toutes celles qui se trouvent sur la dernière ligne, en forme de « L » en quelque sorte. Pour trouver le PPCM, vous devez multiplier entre eux tous ces facteurs [5] .
- Vous voyez que 2 et 3 sont dans la première colonne de la grille et que 3 et 5 sont dans la dernière rangée. La formule de calcul est la suivante :
-
8Faites le calcul. Après avoir vérifié que vous avez bien sélectionné les bons facteurs, procédez aux multiplications et vous aurez le plus petit commun multiple de vos deux nombres de départ [6] .
- Faites le calcul : . En conclusion, le plus petit commun multiple de 18 et 30 est donc 90.
Publicité
Méthode 4
Méthode 4 sur 4:Utiliser l'algorithme d'Euclide
-
1Prenez connaissance de quelques éléments de terminologie. Dans une division, il y a toujours un dividende, à savoir le nombre qui est divisé. Celui qui divise est le diviseur et le résultat de la division est le quotient. Si la réponse n'est pas un entier, il y a ce qu'on appelle un « reste » [7] .
- Dans la division :
15 est le dividende
6 est le diviseur
2 est le quotient
3 est le reste.
- Dans la division :
-
2Inscrivez la formule littérale d'une division. La formule est la suivante : [8] . C'est cette formule qui est la base de l'algorithme d'Euclide qui permet de calculer le plus grand commun diviseur de deux nombres.
- Prenons un exemple concret :
- Ce qu'on appelle le plus grand commun diviseur est l'entier le plus important qui divise les deux nombres en question [9] .
- En fait, avec cette méthode, il faut d'abord calculer le plus grand commun diviseur avant de pouvoir calculer le plus petit commun multiple.
-
3Divisez le plus grand des deux nombres par le plus petit. Le premier de ces nombres sera le dividende, et le second, le diviseur. Vous avez une division, vous pouvez donc utiliser la formule établie précédemment.
- Admettons qu'on vous donne à calculer le plus petit commun multiple de 210 et de 45. Une fois les calculs faits, la formule ressemble à :
-
4Faites une seconde division. Le dividende sera le diviseur précédent, tandis que le reste sera le diviseur. Vous pouvez à nouveau utiliser la formule établie précédemment.
- Cela donne, calculs faits :
-
5Recommencez ainsi jusqu'à avoir un reste égal à 0. Chaque nouvelle division aura pour dividende le diviseur précédent, et comme diviseur, le reste de la division précédente [10] .
- La troisième division est la suivante : . Le reste étant égal à 0, les calculs s'arrêtent là.
-
6Repérez le dernier diviseur utilisé. C'est lui ! C'est le plus grand commun diviseur de vos deux nombres [11] .
- La dernière division était : , le diviseur était 15. Vous avez là le plus grand commun diviseur de 210 et de 45.
-
7Multipliez les deux nombres de départ. Divisez ce résultat par le plus grand commun diviseur trouvé à l'étape précédente. Ce que vous obtenez est enfin le plus petit commun multiple des deux nombres.
- D'abord, vous multipliez : , puis vous divisez par le plus grand commun diviseur, ce qui donne : . C'est le plus petit commun multiple de 210 et de 45 que vous cherchiez.
Publicité
Conseils
- Si l'on vous demandait de calculer le PPCM de plusieurs nombres, il suffit de modifier les méthodes. Ainsi, si vous devez trouver le PPCM de 16, 20 et 32, vous devriez commencer par trouver le PPCM de 16 et de 20 (soit 80), ensuite de quoi, vous calculez le PPCM de 80 et de 32, ce qui vous donnera 160. 160 est le PPCM de 16, 20 et 32.
- En algèbre, connaitre le PPCM est très utile, en particulier quand il y a des sommes de fractions. Il faut souvent réduire les fractions au même dénominateur pour pouvoir les additionner ou les soustraire. La meilleure façon de faire est de trouver le plus petit commun dénominateur (PPCD) qui n'est rien d'autre, dans ce cas-là seulement, que le plus petit commun multiple.
Références
- ↑ https://www.mathsisfun.com/definitions/multiple.html
- ↑ https://www.mathsisfun.com/least-common-multiple.html
- ↑ https://www.khanacademy.org/math/pre-algebra/pre-algebra-factors-multiples/pre-algebra-lcm/v/least-common-multiple-exercise
- ↑ https://www.youtube.com/watch?v=NKlOm3tPQiw
- ↑ https://www.youtube.com/watch?v=b6qehkDuioQ
- ↑ https://www.youtube.com/watch?v=NKlOm3tPQiw
- ↑ http://www.ducksters.com/kidsmath/division_basics.php
- ↑ https://people.richland.edu/james/lecture/m116/polynomials/zeros.html
- ↑ http://mathworld.wolfram.com/GreatestCommonDivisor.html
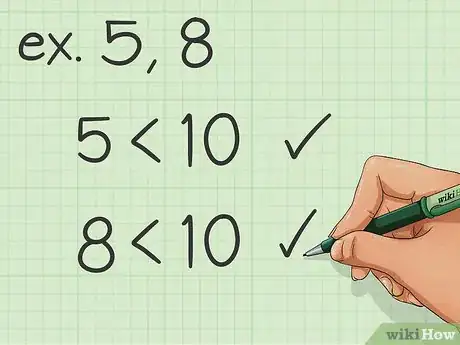


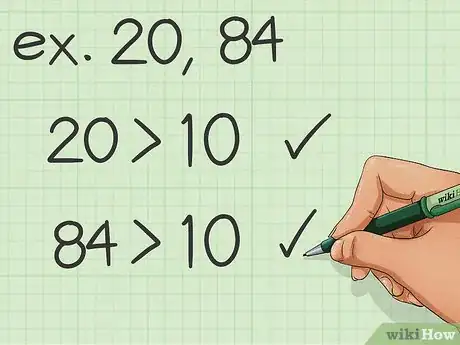
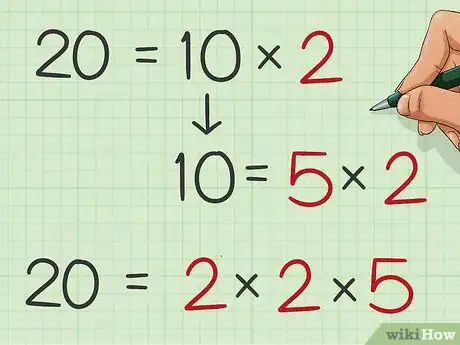



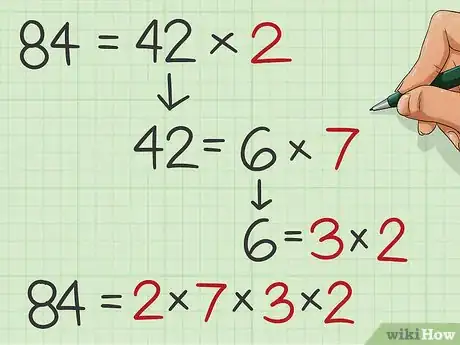




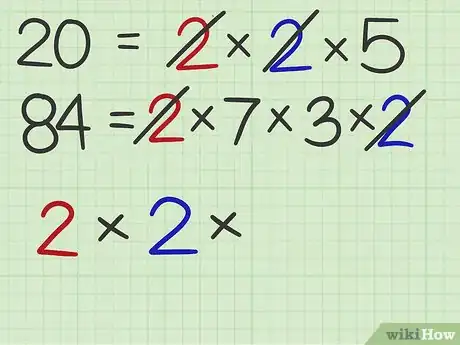


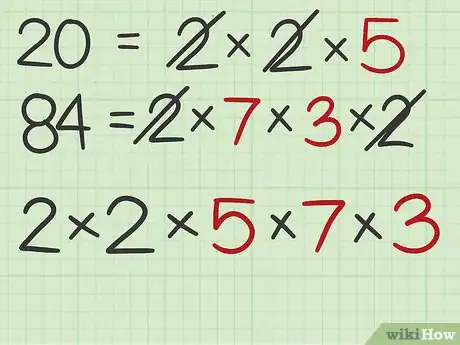




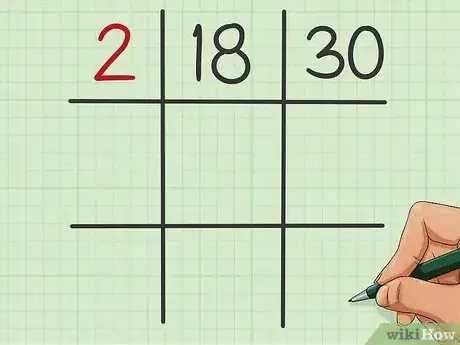


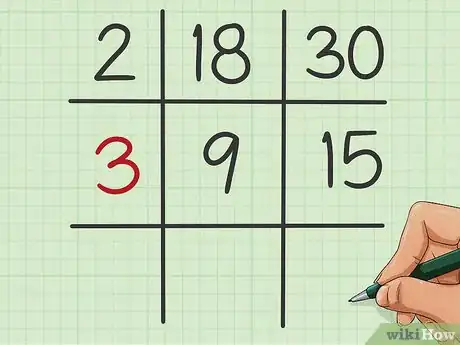






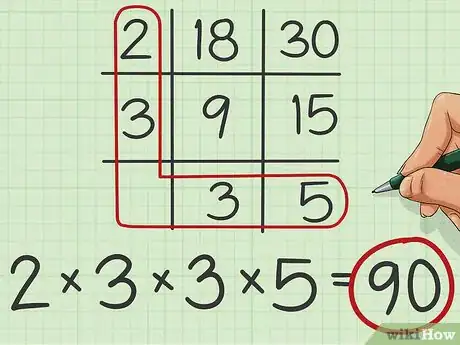






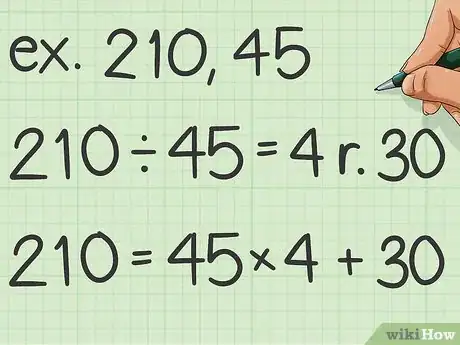





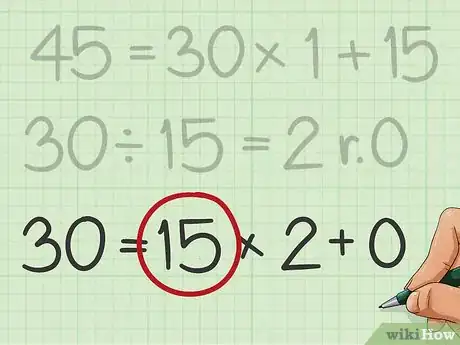

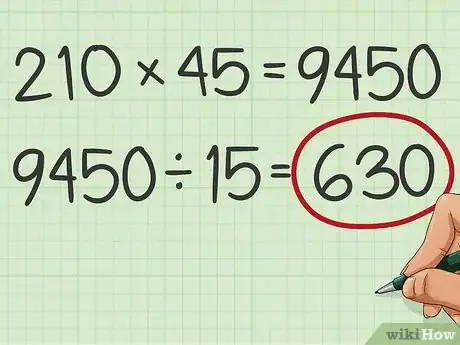





















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 94 901 fois.