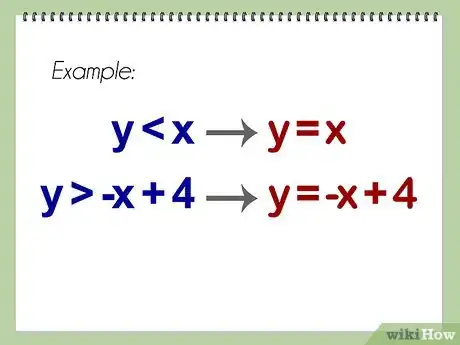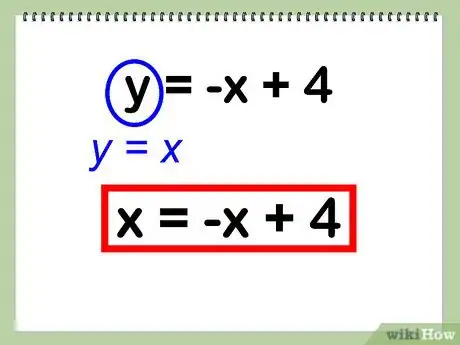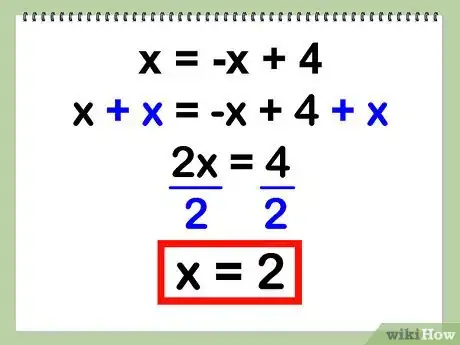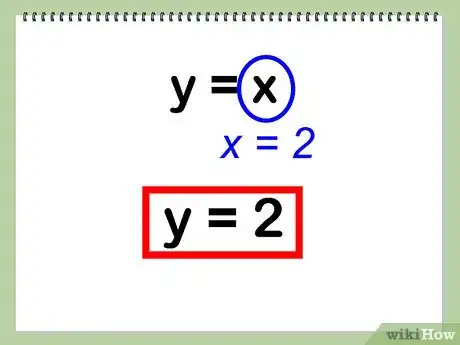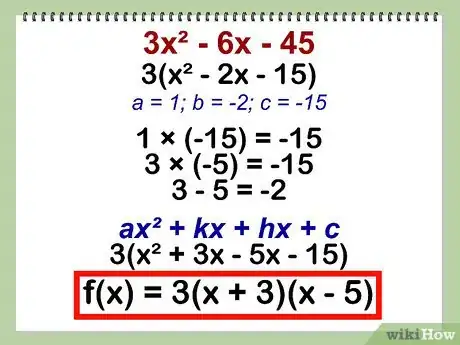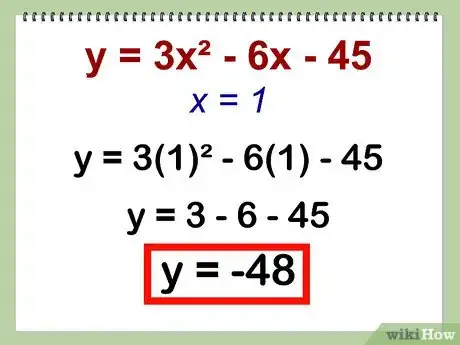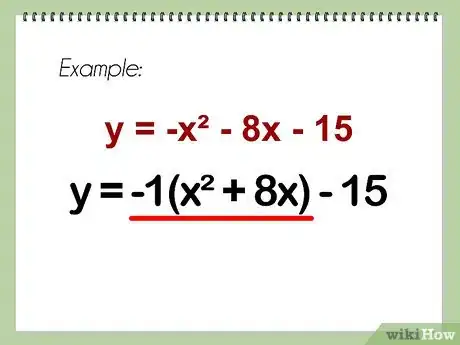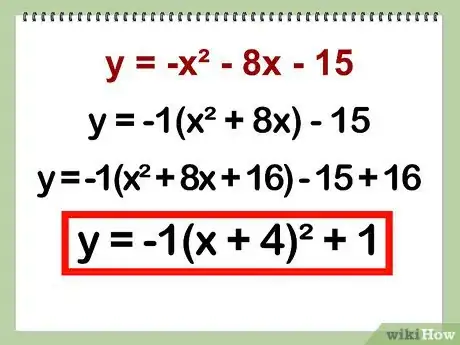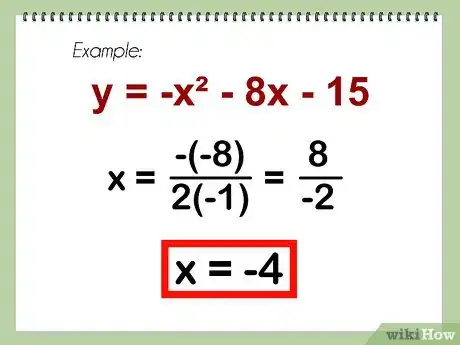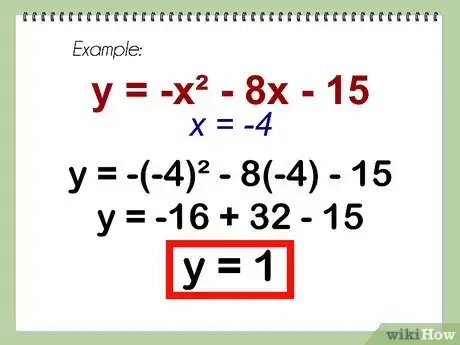X
wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, des auteur.e.s volontaires ont participé à l'édition et à l'amélioration.
Cet article a été consulté 6 382 fois.
De nombreuses fonctions mathématiques font apparaitre des sommets. Les polyèdres ont des sommets, les systèmes d'inéquations linéaires aussi, de même les paraboles (qui sont les représentations graphiques d'équations du second degré). Les calculs de ces points particuliers diffèrent selon la fonction mathématique qui s'offre à vous. Nous allons voir, ici, 5 cas de figure
Étapes
Méthode 1
Méthode 1 sur 5:Trouver le nombre de sommets d'un polyèdre
Méthode 1
-
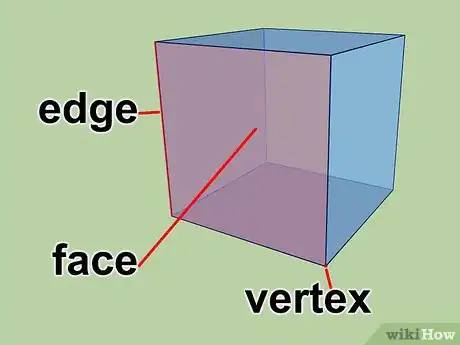
1Prenez connaissance de la formule d'Euler pour les polyèdres. Cette formule établit que, pour n'importe quel polyèdre convexe, le nombre de faces, plus le nombre de sommets, moins le nombre d'arêtes est toujours égal à 2 [1] .
- Écrite sous forme d'équation, la formule est la suivante : f + s - a = 2
- f est le nombre de faces
- s est le nombre de sommets ou de coins
- a est le nombre d'arêtes
- Écrite sous forme d'équation, la formule est la suivante : f + s - a = 2
-
2Manipulez l'équation pour isoler le nombre de sommets ("s"). Si les nombres de faces ("f") et d'arêtes ("a") vous sont donnés, vous allez, grâce à la formule d'Euler, calculer facilement le nombre de sommets. Vous passez "f" et "a" de l'autre côté de l'équation en changeant leurs signes, et le tour est joué !
- s = 2 - f + a
-
3Faites l'application numérique et résolvez l'équation. Si on vous donne "f" et "a", il ne vous reste plus qu'à les mettre dans l'équation et faire les calculs. Vous obtiendrez ainsi le nombre de sommets.
- Exemple : vous avez un a polyèdre à 6 faces et 12 arêtes...
- s = 2 - f + a
- s = 2 - 6 + 12
- s = -4 + 12
- s = 8
Publicité - Exemple : vous avez un a polyèdre à 6 faces et 12 arêtes...
Méthode 2
Méthode 2 sur 5:Trouver les sommets d'un système d'inéquations linéaires
Méthode 2
-
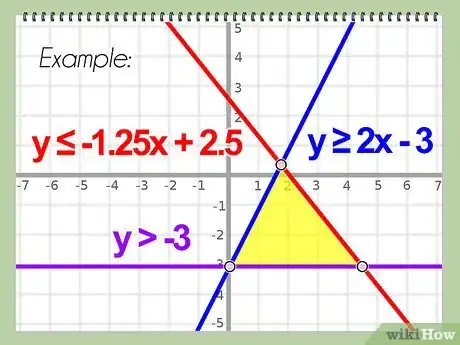
1Tracez les graphes des différentes inéquations linéaires. Ainsi, vous pourrez voir certains ou tous les sommets (ici, ce sont des points d'intersection), tout dépend des équations et de la taille de votre graphique. Si vous n'en voyez aucun, c'est qu'ils sont en dehors de votre graphique, il faut donc les calculer.
- À l'aide d'une calculatrice graphique, vous allez pouvoir visualiser les sommets des différentes courbes (s'il y en a) et lire leurs coordonnées.
-
2Transformez les inéquations en équations. Pour résoudre un système d'inéquations, vous devez provisoirement transformer les inéquations en équations, afin de pouvoir calculer x et y.
- Exemple : Soit le système d'inéquations suivant…
- y < x
- y > -x + 4
- On transforme les inéquations en équations :
- y = x
- y = -x + 4
- Exemple : Soit le système d'inéquations suivant…
-
3Remplacez une des inconnues dans l'autre équation. Bien qu'il y ait différentes façons de procéder, nous allons voir la méthode dite de "substitution" des x et des y, la plus simple certainement. Dans la deuxième équation, on va prendre pour y la valeur qu'elle a dans la première. On substitue y. Cela revient en fait à rendre égales les deux équations.
- Exemple :
- y = x
- y = -x + 4
- Par substitution, y = -x + 4 devient :
- x = -x + 4
- Exemple :
-
4Trouvez la valeur de l'inconnue. Maintenant, vous n'avez plus qu'une seule inconnue (x), facile à trouver ici par le jeu des additions, soustractions, multiplications et divisions. C'est une simple équation du premier degré.
- Exemple : x = -x + 4
- x + x = -x + x + 4
- 2x = 4
- 2x / 2 = 4 / 2
- x = 2
- Exemple : x = -x + 4
-
5Trouvez la seconde inconnue. Prenez la valeur que vous venez de trouver et mettez-la dans l'une des deux équations afin de déterminer y.
- Exemple : y = x
- y = 2
- Exemple : y = x
-
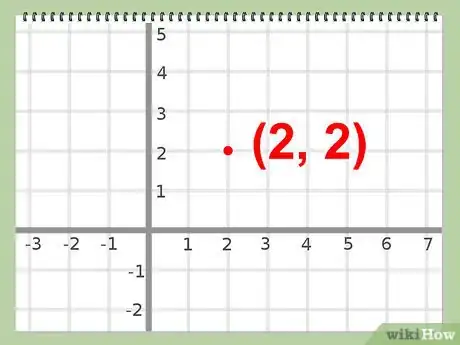
6Déterminez le sommet. Le sommet a alors pour coordonnées vos deux valeurs, x et y.
- Exemple : (2, 2)
Publicité
Méthode 3
Méthode 3 sur 5:Trouver le sommet d'une parabole connaissant l'axe de symétrie
Méthode 3
-
1Mettez l'équation en facteurs. Récrivez l'équation du second degré sous forme factorisée. Il y a plusieurs façons de factoriser selon l'équation qu'on a au départ. Quoi qu'il en soit, au final, vous devez avoir une équation sous forme de produits.
- Exemple : (en utilisant la décomposition)
- f(x) = 3x2 - 6x - 45
- Mettez 3 en facteur, ce qui donne : 3 (x2 - 2x - 15)
- Multipliez les coefficients de x2 ("a") et de x0 (constante "c"), soit 1 x -15 = -15
- Trouvez deux nombres dont le produit vaut -15 et la somme est égale au coefficient (b) de x1 (ici, b = - 2). 3 et - 5 font l'affaire, puisque 3 x -5 = -15 et 3 + (- 5) = 3 - 5 = - 2
- Dans l'équation, ax2 + kx + hx + c, remplacez "k" et "h" par les valeurs trouvées précédemment, ce qui donne : 3(x2 + 3x - 5x - 15)
- Factorisez. On obtient alors : f(x) = 3(x + 3) (x - 5)
- Exemple : (en utilisant la décomposition)
-
2Trouvez le point d'intersection de la parabole avec l'axe des abscisses (axe des "x") [2] . Trouver ce point consiste à résoudre l'équation : f(x) = 0.
- Exemple : 3 (x + 3)(x - 5) = 0
- х +3 = 0
- х - 5 = 0
- х = -3 et х = 5
- Les racines de l'équation sont donc : (-3, 0) et (5, 0)
- Exemple : 3 (x + 3)(x - 5) = 0
-
3Trouvez le milieu de ces points. L'axe de symétrie de la parabole passera par ce point qui se trouve au milieu des deux racines. Cet axe est fondamental, puisque le sommet se trouve dessus par définition.
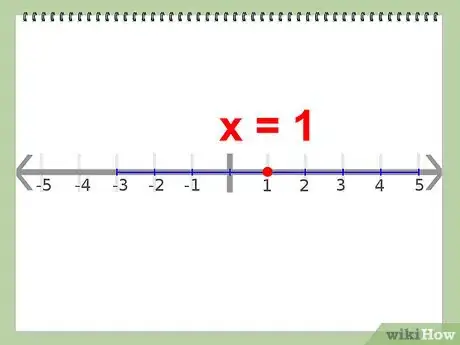
- Exemple : le milieu de -3 et de 5 est : x = 1 [(-3+5)/2 = 2/2 = 1]
-
4Dans l'équation de départ, remplacez x par cette valeur de 1. Vous allez trouver une valeur y qui sera l'ordonnée de votre sommet.
- Exemple : y = 3x2 - 6x - 45 = 3(1)2 - 6(1) - 45 = -48
-
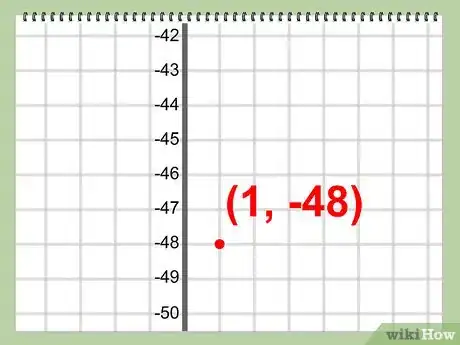
5Inscrivez les coordonnées de votre sommet. Il suffit de réunir les deux valeurs, x et y, pour avoir la position du sommet.
- Exemple : (1, -48)
Publicité
Méthode 4
Méthode 4 sur 5:Trouver le sommet d'une parabole en complétant le carré
Méthode 4
-
1Transformez l'équation de départ sous forme de vertex [3] . Une équation sous forme de "vertex" est du style : y = a(x - h)2 + k, dans laquelle le sommet de la parabole a pour coordonnées (h, k). Il faut donc absolument transformer l'équation de départ pour qu'elle ait une forme de ce type. Pour ce faire, vous allez devoir, ainsi qu'on l'appelle, compléter le carré.
- Exemple : y = -x2 - 8x - 15 (de forme ax2 + bx + c)
-
2Commencez par isoler a. Mettez en facteur, avec les seuls deux premiers termes, le coefficient du terme au second degré (le futur a). Ne touchez pas à la constante c pour l'instant !
- Exemple : -1 (x2 + 8x) - 15
-
3Trouvez un troisième terme pour les parenthèses. Ce terme n'est pas choisi au hasard : il doit être tel qu'il va faire de ce qu'il y a à l'intérieur des parenthèses un carré parfait (ou identité remarquable) de la forme (ax+b)2. Ce nouveau terme à ajouter est le carré de la moitié du coefficient du terme du milieu (b).
- Exemple : b = 8, sa moitié est : 8 / 2 = 4. On prend le carré : 4 x 4 = 16. On obtient ainsi :
- -1(x2 + 8x + 16)
- Pour que l'équation ne soit pas déséquilibrée, ce qu'on a ajouté (ou soustrait) à l'intérieur des parenthèses doit être retiré (ou ajouté) à l'extérieur.
- y = -1(x2 + 8x + 16) - 15 + 16
- Exemple : b = 8, sa moitié est : 8 / 2 = 4. On prend le carré : 4 x 4 = 16. On obtient ainsi :
-
4Effectuez les calculs pour simplifier l'équation. Écrivez l'intérieur des parenthèses sous sa forme de carré parfait et faites la somme des constantes.
- Exemple : y = -1(x + 4)2 + 1
-
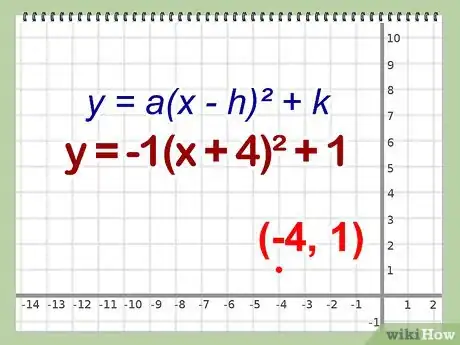
5Trouvez les coordonnées du sommet à partir du vertex. Souvenez-vous ! il nous fallait une équation sous forme de vertex : y = a(x - h)2 + k pour trouver directement les coordonnées (h, k) du sommet. Il suffit alors de lire et parfois de faire un petit calcul pour trouver ces deux valeurs (attention aux signes !).
- k = 1
- h = -4 (-h = 4, donc h = - 4)
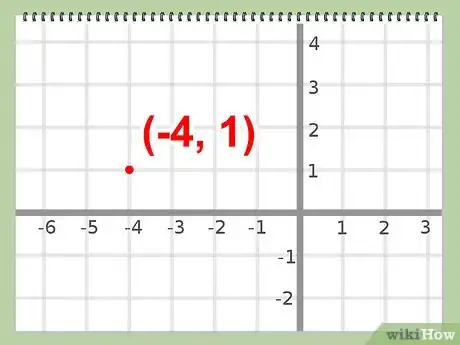
- Pour conclure, le sommet de la parabole se trouve au point de coordonnées (-4, 1)
Publicité
Méthode 5
Méthode 5 sur 5:Trouver le sommet d'une parabole à l'aide d'une formule simple
Méthode 5
-
1Trouvez directement l'abscisse x du sommet. Avec une parabole d'équation y = ax2 + bx + c, l'abscisse x du sommet de la parabole peut être trouvée en utilisant la formule suivante : x = -b / 2a. Il suffit alors de remplacer "a" et "b" par leurs valeurs respectives.
- Exemple : y = -x2 - 8x - 15
- x = -b / 2a = -(-8)/(2 x (-1)) = 8/(-2) = -4
- x = -4
-
2Ensuite, remettez cette valeur de "x" dans l'équation d'origine pour trouver l'ordonnée ("y") du sommet.
- Exemple : y = -x2 - 8x - 15 = -(-4)2 - 8(-4) - 15 = -(16) - (-32) - 15 = -16 + 32 - 15 = 1
- y = 1
- Exemple : y = -x2 - 8x - 15 = -(-4)2 - 8(-4) - 15 = -(16) - (-32) - 15 = -16 + 32 - 15 = 1
-
3Inscrivez alors votre résultat, à savoir les coordonnées du sommet. C'est donc le point de coordonnées ("x","y").
- Exemple : (-4, 1)
Publicité
Éléments nécessaires
- Une calculatrice
- Un stylo
- Du papier
Références
À propos de ce wikiHow
Publicité