Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 13 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 114 055 fois.
En mathématiques, lors de l'analyse d'une fonction, vous pouvez être amené(e) à déterminer le point d'inflexion afin de tracer la courbe de la fonction. Un point d'inflexion est un point où la courbe change de convexité [1] . Dit comme cela, ce point d'inflexion semble un peu abstrait, mais en fait il sert dans de nombreux domaines, comme la chimie (dosage), l'économie, le génie mécanique (came à rainure)… Trouver un point d'inflexion n'est pas très compliqué… à la condition de savoir dériver une fonction.
Étapes
Méthode 1
Méthode 1 sur 5:Bien maitriser la terminologie et les concepts
-
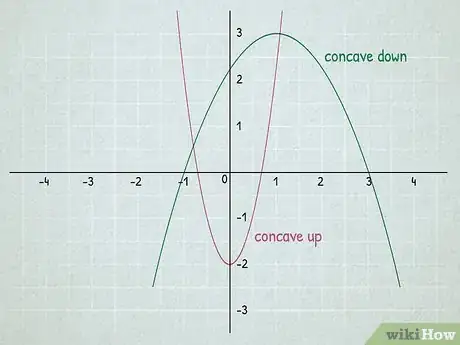
1Faites la différence entre concavité et convexité. Il faut absolument connaitre ces deux concepts pour comprendre le point d'inflexion. Il est un petit moyen mnémotechnique pour retenir la concavité : la courbe est Creuse comme le C de conCavité [2] .
- Une fonction , définie et dérivable sur un intervalle , est concave sur si sa représentation graphique est entièrement située en dessous de chacune de ses tangentes. Sur une courbe, cela se présente sous la forme d'un dôme ou d'une colline.
- À l'inverse, une fonction , définie, dérivable sur un intervalle est convexe sur si sa représentation graphique est entièrement située au-dessus de chacune de ses tangentes. Sur une courbe, cela se présente sous la forme d'un creux.
- Ci-dessus, la courbe rouge est convexe, tandis que la verte est concave.
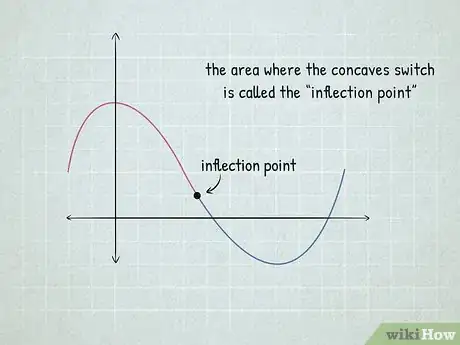
- Sur la courbe d'une fonction, si vous avez une partie convexe (sur un intervalle donné), puis une partie concave (sur un intervalle suivant), à la jonction des deux parties, vous avez ce que l'on appelle un point d'inflexion. Celui-ci marque donc un changement de convexité.
-
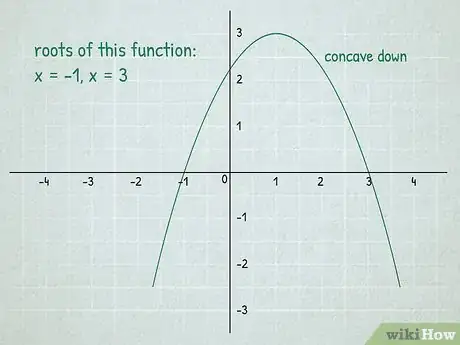
2Appuyez-vous sur les racines de la fonction. Une racine est la valeur de qui annule la fonction. Dans l'illustration ci-dessus, il y a deux racines, à savoir et . Ce sont les points d'intersection du graphe avec l'axe des abscisses [3] .
- Une fonction peut avoir 1, 2, 3 racines, mais aussi aucune !
-
3Cherchez l'inflexion au changement de convexité. Bien entendu, il faut, sur un graphe, être capable de différencier la concavité de la convexité : à la jonction des deux, vous trouverez le point d'inflexion [4] .
- Un point d'inflexion (potentiel) est assez facile à repérer sur une courbe.
Publicité
Méthode 2
Méthode 2 sur 5:Calculer les dérivées d'une fonction
-
1Calculez la dérivée première. Un point d'inflexion ne peut se déterminer qu'à l'aide de la dérivée première de la fonction, ce qui signifie en clair qu'il faut savoir dériver si vous voulez déterminer précisément un point d'inflexion [5] . Une dérivée première est notée ou .
- Prenons l'exemple de la fonction suivante :
- .
- Établissez la dérivée de cette fonction :
- .
- Prenons l'exemple de la fonction suivante :
-
2Calculez la dérivée seconde. Celle-ci est la dérivée de la dérivée et est notée ou .
-
3Déterminez l'abscisse qui annule la dérivée seconde. L'opération consiste à calculer . La réponse est peut-être un point d'inflexion [6] .
- Ici, on part de , soit , soit .
Publicité
Méthode 3
Méthode 3 sur 5:Trouver un point d'inflexion
-
1Voyez si la dérivée seconde change de signe en ce point. Si c'est le cas, alors la courbe contient un point d'inflexion. Par contre, si ce n'est pas le cas, alors il n'y a pas de point d'inflexion : c'est aussi simple que cela [7] !
- Dans cette partie de l'analyse, vous n'allez pas vous intéresser à la valeur obtenue, mais bien au signe du résultat. Parfois, la dérivée seconde est compliquée et la recherche de son signe sur tel ou tel intervalle est complexe. Essayez alors de voir si à vue d'œil certains termes ne seraient pas ou toujours positifs ou toujours négatifs, ce qui vous faciliterait bien la tâche.
- Avec , chaque fois que vous prenez un négatif, est aussi négatif et pour tout positif, vous avez positif. La conséquence en est que le point d'abscisse est le point d'inflexion de la courbe de la fonction
. Vous le voyez, il n'est nul besoin, dans ce cas très précis, de prendre des valeurs de particulières.
-
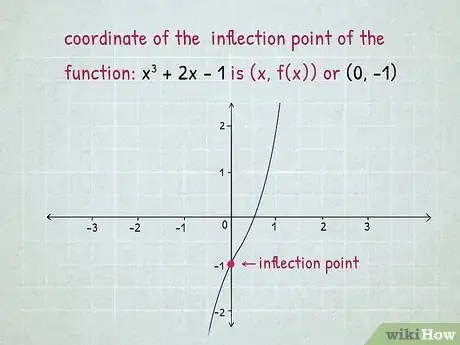
2Cherchez l'ordonnée du point d'inflexion. Cela revient à calculer l'image de par la fonction de départ [8] .
-
3Vérifiez sur le graphe. Les coordonnées du point d'inflexion sont en théorie les suivantes : . Dans notre exemple, le point d'inflexion a été déterminé en , ce qui se voit sur le graphe de la fonction, lequel n'est pas forcément très juste, mais le calcul est là pour obtenir une réponse précise [9] .Publicité
Méthode 4
Méthode 4 sur 5:Vérifier l'existence d'un point d'inflexion
-
1Vérifiez la racine 0 de la dérivée seconde. Si vous obtenez cette racine, soyez prudent(e), car c'est un point particulier. Il faut bien étudier la convexité des deux intervalles qui le cernent et vérifier qu'il y a bien un changement de signe à cet endroit [10] .
- Admettons que vous ayez trouvé un point d'inflexion dont l'abscisse est . Vous devez vérifier qu'entre les intervalles et la dérivée seconde change de signe. Alors, seulement, vous pourrez en conclure que 0 est l'abscisse de votre point d'inflexion.
-
2Ne commettez pas d'erreur. Nous avons dit que l'abscisse d'un point d'inflexion était donnée par l'annulation de la dérivée seconde, mais elle peut aussi être une valeur pour laquelle la dérivée seconde n'est pas définie. Si vous rencontrez ce cas et que vous passez outre, parce que la réponse n'est pas dans le domaine de définition, vous aurez une réponse fausse [11] .
- Dans un exercice, vous devez étudier la fonction et surtout de voir si son graphe présente un ou plusieurs points d'inflexion. C'est bien la dérivée seconde, , de la fonction qui vous renseignera sur l'existence ou non d'un point d'inflexion, la dérivée première, , vous permettant seulement de calculer le minimum de la fonction, ce qui ne nous intéresse pas ici.
-
3Analysez la dérivée seconde, non la dérivée première. C'est toujours la dérivée seconde qui permet de statuer sur l'existence ou non d'un ou de plusieurs points d'inflexion (nous ne rentrerons pas dans la distinction qu'il y a entre l'inflexion analytique et géométrique [12] ).
- Admettons qu'une courbe présente deux points d'inflexion, l'un en et l'autre en . Prenez une valeur dans chacun de ces intervalles définis par ces deux points (, et ), déterminez le signe de la dérivée seconde sur chacun, puis vérifiez qu'il y a changement de signe d'un intervalle à l'autre. Alors seulement, vous pourrez en conclure que ces deux abscisses, et , sont celles de vos 2 points d'inflexion.
Publicité
Méthode 5
Méthode 5 sur 5:Trouver un point d'inflexion avec une calculatrice
-
1Accédez à l'écriture de la fonction. Appuyez sur la touche verte (troisième ligne du haut et à droite) présentant un losange, puis sur la touche du haut
F1. Là, vous pouvez entrer 7 fonctions [13] .- Nous prendrons l'exemple de la TI-89. Sur d'autres calculatrices, la procédure est différente : consultez la notice de votre machine pour savoir comment faire.
-
2Entrez votre fonction en y1. S'il y en a déjà une en cet endroit, supprimez-la, puis tapez votre fonction, laquelle viendra s'inscrire après le signe . Si parenthèses il y avait, vous les transcririez telles quelles [14] .
- Prenons comme exemple la fonction suivante : .
-
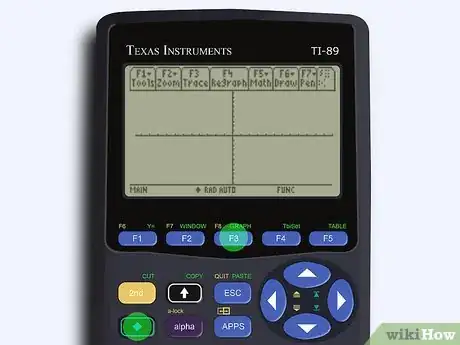
3Tracez la courbe représentative. Pour cela, appuyez sur le losange, puis sur la touche F3. Si la courbe n'apparait pas bien, appuyez sur le losange, puis sur F2 afin de sélectionner 6:Zoomstd (zoom standard [15] ).
- Ne vous affolez pas si la courbe n'est pas entièrement apparente, cela peut facilement s'arranger par la suite !
-
4Réglez la fenêtre d'affichage. Il s'agit de voir l'ensemble de la courbe. Il est fréquent que la courbe n'apparaisse pas dans son entier. Aussi allez-vous régler l'affichage en appuyant sur le losange, puis la touche F2. Avec les touches de navigation, déplacez-vous verticalement dans les différents agrandissements jusqu'à afficher celui qui vous intéresse [16] .
- Il n’est pas toujours très simple, surtout avec le manque d'habitude, d'utiliser cette fonction. Ce n'est pas grave dans la mesure où vous pouvez toujours revenir en arrière.
-
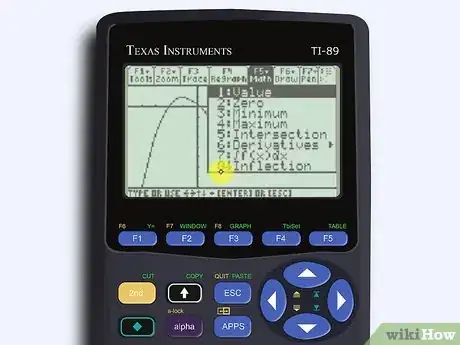
5Affichez le menu Math. Appuyez sur le losange, puis sur la touche F5. À l'aide des flèches de navigation, descendez jusqu'à 8 : Inflexion [17] .
- Cette fonction est très sympathique, mais elle suppose que vous connaissiez la position du point d'inflexion : la machine a ses limites !
-
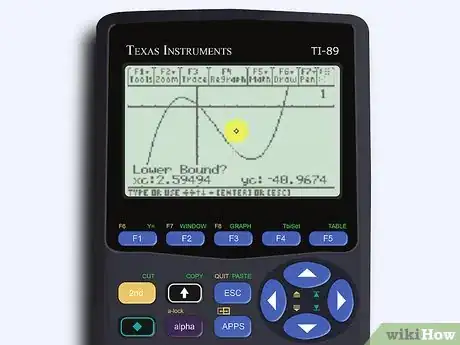
6Déterminez les bornes du point d'inflexion. Cette opération suppose que vous connaissiez la position, même très approximative, du point d'inflexion. Amenez le curseur sur un point de la courbe qui est à droite du point d'inflexion, puis validez avec ↵ Enter. Faites la même chose avec un point de la courbe situé à gauche du point d'inflexion et validez. Si tout s'est bien passé, vous allez voir apparaitre en bas et à gauche de l'écran, les coordonnées du point d'inflexion supposé [18] .
- Si vous pensez qu'il y a un ou plusieurs autres points d'inflexion (sinusoïde), vous recommenceriez la même opération avec les bornes d'un autre supposé point d'inflexion.
Publicité
Conseils
- Il est possible de vérifier la réalité d'un point d'inflexion avec la dérivée tierce
(). Encore faut-il, entre autres conditions, que la fonction de départ soit dérivable trois fois et avec certaines fonctions, cela relève du casse-tête ! - Les fonctions linéaires n'ont pas de point d'inflexion et cela provient du fait que ces fonctions ont toujours la même pente. Ainsi donc, il n'y a pas de changement de pente, condition minimale pour avoir un point d'inflexion.
Références
- ↑ https://www.mathsisfun.com/calculus/inflection-points.html
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6b/a/concavity-review
- ↑ http://www.easy-math.net/root-of-a-function/
- ↑ https://www.youtube.com/watch?v=mXnH_8yxFag
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6a/v/inflection-points
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6b/a/inflection-points-review
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6b/a/review-analyzing-the-second-derivative-to-find-inflection-points
- ↑ https://www.mathsisfun.com/calculus/inflection-points.html
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6b/a/inflection-points-review
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6b/a/review-analyzing-the-second-derivative-to-find-inflection-points
- ↑ https://fr.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6b/a/review-analyzing-the-second-derivative-to-find-inflection-points
- ↑ https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/graphingdirectory/Graphing.html
- ↑ https://www.youtube.com/watch?v=OeD3_Es4J54&feature=youtu.be&t=15
- ↑ https://www.youtube.com/watch?v=OeD3_Es4J54&feature=youtu.be&t=32
- ↑ https://www.youtube.com/watch?v=OeD3_Es4J54&feature=youtu.be&t=32
- ↑ https://www.youtube.com/watch?v=OeD3_Es4J54&feature=youtu.be&t=81
- ↑ https://www.youtube.com/watch?v=IBqCV5WlwUY&feature=youtu.be&t=29
- ↑ https://www.youtube.com/watch?v=IBqCV5WlwUY&feature=youtu.be&t=46










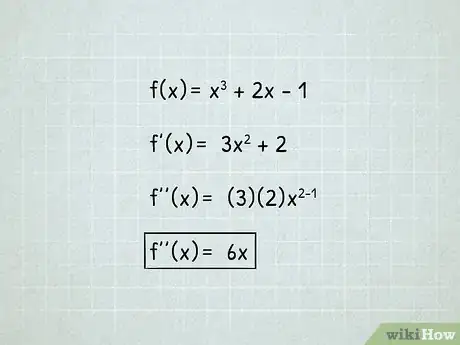















![{\displaystyle ]-\infty ,0[}](./images/1715085158-83a3a204074bde51e56b7965e8c98a66888bbf88.webp)
![{\displaystyle ]0,+\infty [}](./images/2172657717-e91ea5ab8b69e30f90c2bdf5db4b620815bde815.webp)




![{\displaystyle ]-\infty ,-1[}](./images/1460019030-965141b157d9743231e559482f1dbce27bef8ce4.webp)
![{\displaystyle ]-1,7[}](./images/1862606819-ecf49959a755d2534823cfd49890cfa11dab5b1c.webp)
![{\displaystyle ]7,+\infty [}](./images/1762336575-2693c311ed1b96d80aeb05aff085955062544a2c.webp)

























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 114 055 fois.