Comment trouver les racines des polynômes de degré 2 et 3

Informations concernant l'auteur.e

Résoudre un polynôme, c'est trouver tous les points d'intersection entre une ordonnée horizontale placée sur la graduation et la courbe de ce polynôme.

Partie 1

Partie 1 sur 2:
Effectuer une approche géométrique

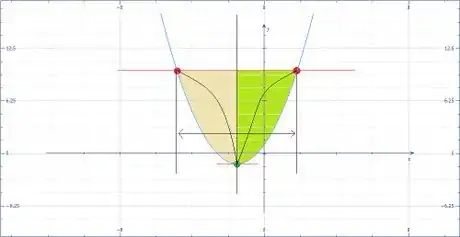
1
L'approche géométrique montre la symétrie qui existe sur un polynôme d'ordre 2.
- Dans la zone beige, le curseur est déplacé vers la gauche et pour chaque solution, la zone verte déplace le curseur vers la droite avec la même distance. Aussi, la somme des deux est toujours nulle : $\Delta x_{1}+\Delta x_{2}=0$
- Si ça fonctionne avec l'ordre 2, ça fonctionne aussi pour les polynômes d'ordre supérieurs.
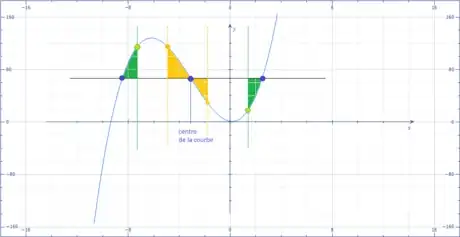
2
Pour un polynôme d'ordre 3 irréductible, la courbe résultante présente deux vague inversées et symétriques.
- Le curseur est déplacé vers la gauche et vers la droite et les distances entre ordonnées sont conservées.
Publicité

Partie 2

Partie 2 sur 2:
Effectuer une approche algébrique

1
Ecrivez les équations différentielles et la différence entre 2 sommes de cubes
- Polynôme 3
  
  $f(x)=x^{3}+b*x^{2}+c*x+d$
- Calculez
  
  $f(x)-f(x_{0})$
- Calculez
  
  $[u+m]^{3}-[u+k]^{3}$
- Factorisez
  
  $m-k$
- Identifier
  
  $m=x,k=x_{0}$
- Trouvez l'équation pour $u$
  
  $u={\frac {b}{3a}}$
- Trouvez une équation pour $x_{0}$
  
  $x_{0}=\pm {\sqrt {\frac {3ac-b^{2}}{3a^{2}}}}$
- En déduire l'équation pour $x$
  
  $x={\sqrt[{3}]{y-f(x_{0})+[u+x_{0}]^{3}}}-u$

Conclusion

Pour tous les polynômes d'ordre 2.
- Un point unique sur la courbe.
- Une solution positive et négative.
- $X=\pm {\sqrt {Y-f(p_{1})+({\frac {f'(p_{1})}{2}})^{2}}}-{\frac {f'(p_{1})}{2}}+p_{1}$
- Valeur négative sous la racine --> Y hors de la courbe.
Pour tous les polynômes irréductibles ou non d'ordre 3.
- 1 à 4 solutions.
- Valeur négative sous la racine carrée --> 1 unique Y réel inexistant
Pour les polynômes supérieurs, méthode commune et récursive
- Calculez la différence entre deux sommes $[u+m]$ et $[u+k]$ élevés à la puissance du plus grand degré du polynôme.
- Diminution du degré de 1 : degré N --> degré N-1