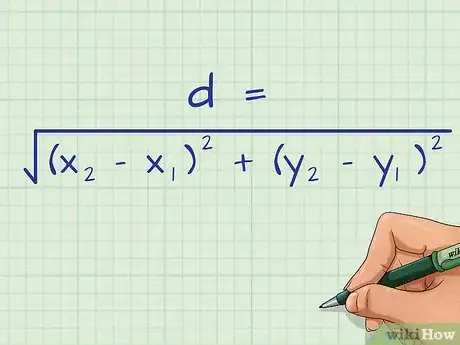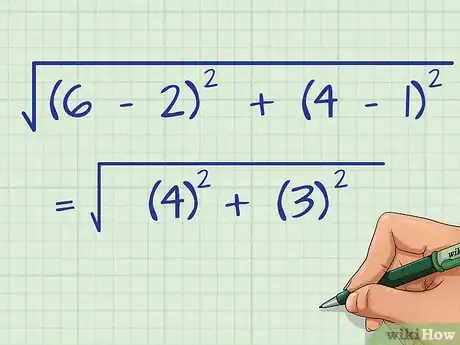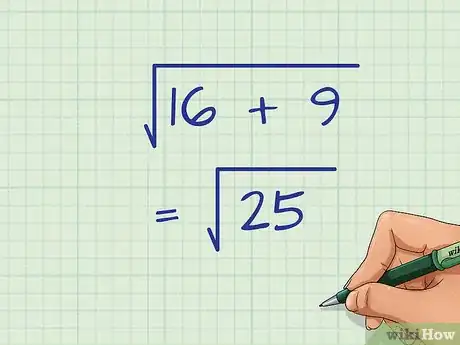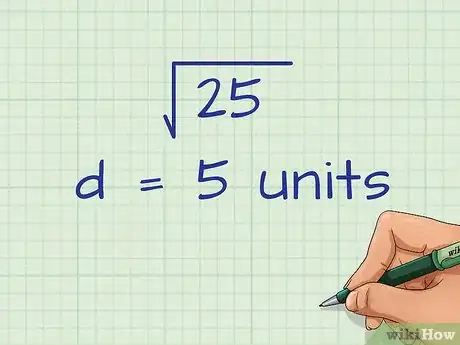Comment utiliser la formule de la distance entre deux points

Coécrit par Christopher M. Osborne, PhD

Dans un plan cartésien, on peut mesurer la longueur d’un segment horizontal ou vertical simplement en lisant ses coordonnées. En revanche, on ne peut pas faire la même chose pour un segment en diagonale. Il faut alors se servir de la formule de la distance entre deux points, qui est en fait une application du théorème de Pythagore. Pour mieux le comprendre, vous pouvez imaginer que le segment dont vous cherchez la longueur est aussi l’hypoténuse d’un triangle rectangle ^{[1]
X
Source de recherche}. À l’aide d’une formule de géométrie assez simple, vous allez réussir à mesurer sans difficulté des distances sur un repère orthonormé.

Partie 1

Partie 1 sur 2:
Comprendre la formule

1
Reprenez la formule de la distance entre deux points. Elle s’écrit $d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$ , $d$ étant la longueur du segment, $(x_{1},y_{1})$ étant les coordonnées du point qui se trouve à la première extrémité du segment, et $(x_{2}y_{2})$ étant les coordonnées du point qui se trouve à sa seconde extrémité ^{[2]
X
Source de recherche}.
2
Trouvez les coordonnées nécessaires. Vous avez besoin de connaitre les coordonnées des points situés aux deux extrémités du segment. Elles sont parfois données dans l’énoncé. Si ce n’est pas le cas, reportez-vous à l’axe des x et à l’axe des y pour les lire.
- Dans un repère orthonormé, l’axe des y est vertical et l’axe des x est horizontal.
- Les coordonnées d’un point doivent être écrites sous la forme $(x,y)$ .
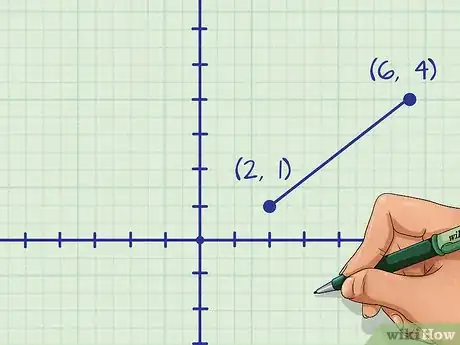
- Il se peut par exemple qu’un segment de droite soit délimité par deux points dont les coordonnées seront $(2,1)$ pour le premier, et $(6,4)$ pour le second.
3
Placez les coordonnées dans la formule. Veillez bien à intégrer vos données dans la formule à la bonne place. Les deux coordonnées que vous avez lues sur l’axe des $x$ $x$ doivent se trouver dans la première parenthèse, tandis que les deux coordonnées que vous avez lues sur l’axe des $y$ $y$ doivent se trouver dans la seconde.
- Par exemple, pour les points $(2,1)$ et $(6,4)$ , cela donnera dans votre formule : $d={\sqrt {(6-2)^{2}+(4-1)^{2}}}$ .
Publicité

Partie 2

Partie 2 sur 2:
Calculer la distance

1
Faites les soustractions. En raison des règles de priorité dans l’ordre des opérations, vous devez en tout premier lieu faire les calculs qui se trouvent à l’intérieur des parenthèses.
- Par exemple :
  $d={\sqrt {(6-2)^{2}+(4-1)^{2}}}$
  $d={\sqrt {(4)^{2}+(3)^{2}}}$
2
Mettez au carré. Prenez les valeurs que vous avez trouvées dans les parenthèses et mettez-les au carré. Les règles de priorité vous obligent à réaliser en second lieu le calcul des nombres ayant un exposant.
- Par exemple :
  $d={\sqrt {(4)^{2}+(3)^{2}}}$
  $d={\sqrt {16+9}}$
3
Ajoutez les nombres sous la racine. Faites ce calcul exactement de la même façon que si vous étiez en présence de nombres qui ne sont pas sous une racine carrée.
- Par exemple :
  $d={\sqrt {16+9}}$
  $d={\sqrt {25}}$
4
Trouvez $d$ . Pour obtenir le résultat final, trouvez la racine carrée de la somme précédente.
- Étant donné qu’il s’agit d’une racine carrée, il se peut que vous deviez arrondir votre réponse.
- N’oubliez pas que vous vous trouvez dans un repère orthonormé, votre réponse devra donc être exprimée en « unités », sans plus de précisions, et non en mètres ou en centimètres.
- Par exemple :
  $d={\sqrt {25}}$
  $d=5$ unités
Publicité

Conseils

Ne mélangez pas cette formule avec d’autres, par exemple avec la formule du milieu d’un segment, la formule de la pente, ou avec une équation linéaire.
Veillez à respecter l’ordre de priorité des opérations lorsque vous faites votre calcul. Faites d’abord les soustractions, puis mettez leurs résultats au carré, additionnez et terminez par trouver la racine carrée.