قيم جبرية دقيقة لثوابت مثلثية
التعبيرات الجبرية الدقيقة للقيم المثلثية مفيدة في بعض الأحيان، خاصةً لتبسيط الحلول إلى أشكال جذرية تسمح بمزيد من التبسيط.
| جزء من سلسلة مقالات حول |
| حساب المثلثات |
|---|
 |
| بوابة رياضيات |

جميع الأعداد المثلثية - الجيب أو جيب التمام من مضاعفات كسرية لـ 360° - هي أعداد جبرية (حلول المعادلات متعددة الحدود مع معاملات صحيحة)؛ زيادة على ذلك، يمكن التعبير عنها بدلالة جذور الأعداد المركبة؛ ولكن ليس كل هذه يمكن التعبير عنها بدلالة جذور حقيقية. عندما تكون كذلك، فهي قابلة للتعبير بشكل أكثر تحديدًا بدلالة الجذور التربيعية.
جميع قيم الجيب، وجيب التمام، وظلال الزوايا متزايدة بـ 3° يمكن تعبير عنها بدلالة الجذور التربيعية، باستخدام المتطابقات (متطابقة نصف الزاوية، ومتطابقة ضعف الزاوية، ومتطابقة إضافة/طرح الزاوية) وباستخدام القيم لـ 0° و 30° و 36° و 45° . بالنسبة لزاوية عدد صحيح بالدرجات التي ليست مضاعفة لـ 3° (π60 راديان)، لا يمكن التعبير عن قيم الجيب وجيب التمام والمماس بدلالة الجذور الحقيقية.
وفقًا لمبرهنة نيفن، فإن القيم الكسرية الوحيدة لدالة الجيب التي من أجلها تكون عمدتها (argument) عبارة عن عدد كسري من الدرجات هي: 0، و 12، و 1، -12 و -1.
وفقًا لمبرهنة باكر، إذا كانت قيمة الجيب أو جيب التمام أو الظل جبرية، فإن الزاوية تكون إما عددًا نسبيًّا من الدرجات أو عددًا متساميًا من الدرجات. وبعبارة أخرى، إذا كانت الزاوية عبارة عن عدد جبري من الدرجات، ولكنها غير كسرية، فإن جميع الدوال المثلثية لها قيم متسامية.
جدول بعض الزوايا الشائعة
عدة وحدات القياس زاوية تستخدم على نطاق واسع، بما في ذلك الدرجات، الراديات، والغراد:
1 دائرة كاملة (دورة) = 360 درجات = 2π راديان = 400 غراد.
يعرض الجدول التالي التحويلات والقيم لبعض الزوايا الشائعة:
دورات درجات راديان غراد جيب جيب التمام ظل 0 0° 0 0g 0 1 0 112 30° π6 3313g12 √32
√33
18 45° π4 50g √22√221 16 60° π3 6623g√3212 √314 90° π2 100g 1 0 13 120° 2π3 13313g√32−12−√338 135° 3π4 150g √22−√22−1512 150° 5π6 16623g12 −√32−√3312 180° π 200g 0 −10 712 210° 7π6 23313g−12−√32√3358 225° 5π4 250g −√22−√221 23 240° 4π3 26623g−√32−12√334 270° 3π2 300g −10 56 300° 5π3 33313g−√3212 −√3
78 315° 7π4 350g −√22√22−11112 330° 11π6 36623g−12√32−√331 360° 2π 400g 0 1 0
زوايا أخرى

0 °: أساسي
- غير معرف
1.5 °: مئة وعشروني الأضلاع المنتظم (المضلع به 120 ضلع)
1.875 °: ست وتسعوني الاضلاع (مضلع ذو 96 ضلعًا)
2.25 °: المثمن المنتظم (مضلع به 80 ضلع)
2.8125 ° : أربع وستيني الأضلاع المنتظم (مضلع ذو جانبين)
3 °: ستيني الأضلاع المنتظم (مضلع به 60 ضلع)
3.75 °: ثماني وأربعيني الأضلاع المنتظم (مضلع ذو 48 ضلعًا)
4.5 °: أربعيني الأضلاع المنتظم (مضلع ذو 40 ضلعًا)
5.625 °: إثنا وثلاثيني الأضلاع (مضلع ذو 32 ضلعًا)
6 °: ثلاثيني الأضلاع المنتظم (مضلع ذو 30 ضلعًا)
7.5 °: أربع وعشريني الأضلاع المنتظم (مضلع ذو 24 ضلعًا)
9 °: عشروني الأضلاع المنتظم (مضلع ذو 20 ضلعًا)
11.25 °: ستة عشري الأضلاع المنتظم
12 °: خمسة عشري الأضلاع المنتظم
15 °: إثنا عشري الأضلاع المنتظم
18 °: عشري الأضلاع منتظم [1]
21 °: مجموع 9 درجة + 12 درجة
24 °: مجموع 12 درجة + 12 درجة
27 °: مجموع 12 درجة + 15 درجة
30 °: المسدس المنتظم
33 °: مجموع 15 درجة + 18 درجة
39 °: مجموع 18 درجة + 21 درجة
42 °: مجموع 21 درجة + 21 درجة
45 °: مربع
54 °: مجموع 27 درجة + 27 درجة
60 °: مثلث متساوي الأضلاع
67.5 °: مجموع 7.5 درجة + 60 درجة
72 °: مجموع 36 درجة + 36 درجة
75 °: مجموع 30 درجة + 45 درجة
90 °: أساسي
- غير معرف
قائمة الثوابت المثلثية لـ 2πn
بالنسبة إلى الجذور التكعيبية للأعداد غير الحقيقية التي تظهر في هذا الجدول، يجب أخذ القيمة الأساسية، وهذا يعني أن الجذر التكعيبي يحتوي على أكبر جزء حقيقي؛ هذا الجزء الأكبر الحقيقي هو دائما موجب. لذلك، فإن مجموع الجذور التكعيبية التي تظهر في الجدول كلها أعداد حقيقية موجبة.
ملاحظات
استخدامات الثوابت
كمثال على استخدام هذه الثوابت، نعتبر حجم إثنا عشري السطوح المنتظم [الإنجليزية]، حيث a هو طول إحدى أحرفه:
باستخدام:
يمكن تبسيط هذا إلى:
اشتقاق القيم من المثلثات
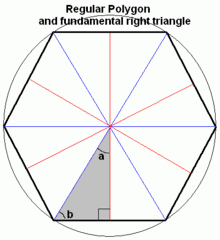
يعتمد اشتقاق القيم الدقيقة للجيب وجيب التمام والظل على إنشاء المثلثات القائمة.
هنا تستخدم المثلثات القائمة التي أنشئت من قِطَع التناظر للمضلعات العادية لحساب النسب المثلثية الأساسية. يمثل كل مثلث قائم ثلاث نقاط في مضلع عادي: الرأس، مركز الحافة الحاوية لهذا الرأس، ومركز المضلع. يمكن تقسيم مضلع ذو n ضلعًا إلى 2n مثلثات قائمة ذات زوايا 180n، و 90 − 180n، و 90° ، من أجل n = 3 , 4 , 5 , ....
قابلية إنشاء المضلعات ذات 3 و 4 و 5 و 15 ضلعًا هي الأساس، كما تسمح منصفات الزوايا باشتقاق مضاعفات تلك أعداد الأضلاع في اثنين أيضًا.
- القابلة للإنشاء
- مضلعات منتظمة ذات 3 × 2n ضلعًا، من أجل n = 0, 1, 2, 3, ...
- مثلث ذو زوايا 30°-60°-90° : مثلث
- مثلث ذو زوايا 60°-30°-90° : سداسي (ذو 6 أضلاع)
- مثلث ذو زوايا 75°-15°-90° : إثنا عشري الأضلاع
- مثلث ذو زوايا 82.5°-7.5°-90° : أربعة وعشروني الأضلاع
- مثلث ذو زوايا 86.25°-3.75°-90° : ثمانية وأربعوني الأضلاع
- مثلث ذو زوايا 88.125°-1.875°-90° : ستة وتسعوني الأضلاع
- مثلث ذو زوايا 89.0625°-0.9375°-90° : ذو 192 ضلعًا
- مثلث ذو زوايا 89.53125°-0.46875°-90° : ذو 384 ضلعًا
- ...
- ذو 4 × 2n ضلعًا
- مثلث ذو زوايا 45°-45°-90° : مربع
- مثلث ذو زوايا 67.5°-22.5°-90° : ثماني الأضلاع
- مثلث ذو زوايا 78.75°-11.25°-90° : ستة عشري الأضلاع
- مثلث ذو زوايا 84.375°-5.625°-90° : إثنان وثلاثوني الأضلاع
- مثلث ذو زوايا 87.1875°-2.8125°-90° : أربعة وستوني الأضلاع
- مثلث ذو زوايا 88.09375°-1.40625°-90° : ذو 128 ضلعًا
- مثلث ذو زوايا 89.046875°-0.703125°-90° : ذو 256 ضلعًا
- ...
- ذو 5 × 2n ضلعًا
- مثلث ذو زوايا 54°-36°-90° : خماسي الأضلاع
- مثلث ذو زوايا 72°-18°-90° : عشري الأضلاع
- مثلث ذو زوايا 81°-9°-90° : عشروني الأضلاع
- مثلث ذو زوايا 85.5°-4.5°-90° : أربعوني الأضلاع
- مثلث ذو زوايا 87.75°-2.25°-90° : ثمانوني الأضلاع
- مثلث ذو زوايا 88.875°-1.125°-90° : ذو 160 ضلعًا
- مثلث ذو زوايا 89.4375°-0.5625°-90° : ذو 320 ضلعا
- ...
- ذو 15 × 2n ضلعًا
- مثلث ذو زوايا 78°-12°-90° : خمسة عشري الأضلاع
- مثلث ذو زوايا 84°-6°-90° : ثلاثوني الأضلاع
- مثلث ذو زوايا 87°-3°-90° : ستوني الأضلاع
- مثلث ذو زوايا 88.5°-1.5°-90° : ذو 120 ضلعًا
- مثلث ذو زوايا 89.25°-0.75°-90° : ذو 240 ضلعًا
- ...
- مضلعات منتظمة ذات 3 × 2n ضلعًا، من أجل n = 0, 1, 2, 3, ...
- هناك أيضًا مضلعات منتظمة أخرى قابلة للإنشاء: 17, 51, 85, 255, 257, 353, 449, 641, 1409, 2547, ..., 65535, 65537, 69481, 73697, ..., 4294967295.)
- غير القابلة للإنشاء – التعبيرات الجذرية اللانهائية التي تتضمن أعدادًا حقيقية لتلك نسب أضلاع المثلث ممكنة، وبالتالي فإن مضاعفاتها في اثنين غير ممكنة أيضًا.
- ذو 9 × 2n ضلعًا
- مثلث ذو زوايا 70°-20°-90° : تساعي الأضلاع
- مثلث ذو زوايا 80°-10°-90° : ثمانية عشري الأضلاع
- مثلث ذو زوايا 85°-5°-90° : ستة وثلاثوني الأضلاع
- مثلث ذو زوايا 87.5°-2.5°-90° : إثنا وسبعوني الأضلاع
- ...
- ذو 45 × 2n ضلعًا
- مثلث ذو زوايا 86°-4°-90° : خمسة وأربعوني الأضلاع
- مثلث ذو زوايا 88°-2°-90° : تسعوني الأضلاع [الإنجليزية]
- مثلث ذو زوايا 89°-1°-90° : ذو 180 ضلعًا
- مثلث ذو زوايا 89.5°-0.5°-90° : ذو 360 ضلعًا
- ...
- ذو 9 × 2n ضلعًا
انظر أيضا
- مضلع قابل للإنشاء
- انشاء سبعة عشري الأضلاع، يعطي عبارة دقيقة لـ cos 2π17.
- قائمة المطابقات المثلثية
- مبرهنة نيفن حول القيم الكسرية لجيب مضاعف كسري لـ π
- الدوال المثلثية
المراجع
- Bradie, Brian (سبتمبر 2002)، "Exact values for the sine and cosine of multiples of 18°: A geometric approach"، The College Mathematics Journal، 33 (4): 318–319، doi:10.2307/1559057، JSTOR 1559057.
روابط خارجية
- المضلعات المنتظمة القابلة للإنشاء
- تسمية المضلعات
- يتضمن Sine and cosine in surds تعبيرات بديلة في بعض الحالات وكذلك تعبيرات لبعض الزوايا الأخرى.
- بوابة رياضيات
- بوابة هندسة رياضية
- بوابة جبر