وراثيات سكانية
الوراثيات السكانية (بالإنجليزية: Population genetics) هي مجال فرعي لعلم الوراثة متخصص في الاختلافات الوراثية داخل المجموعات السكانية وفيما بينها، وتُعتبر جزءًا من علم الأحياء التطوري. تختبر دراسات فرع علم الأحياء هذا العديد من الظواهر مثل التكيف، والانتواع والبنية السكانية.[1]
وراثيات سكانية 
|
| جزء من سلسلة مقالات حول |
| التطور |
|---|
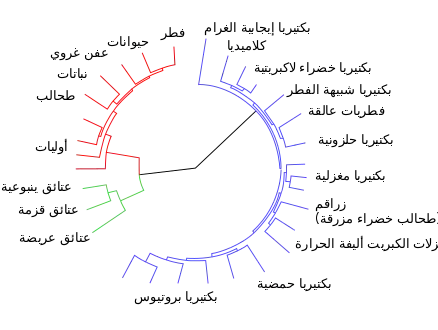 |
| بوابة علم الأحياء التطوري |
شكلت الوراثيات السكانية مكونًا رئيسيًا في تولد الاصطناع التطوري الحديث. أسسها بشكل أساسي كل من سيوال رايت، وجون هولدين ورونالد فيشر، الذي وضع أساسات قواعد علم الوراثة الكمومي. تُعد الوراثيات السكانية الحديثة تخصصًا رياضيًا عالي المستوى، وتشمل العمل النظري والمخبري والميداني. تُستخدم النماذج الوراثية السكانية في كل من الاستدلال الإحصائي من بينات تسلسل الدنا وفي إثبات/دحض المفاهيم.[2]
ما يميز الوراثيات السكانية عن النُهج الأحدث المعتمدة على الأنماط الظاهرية، مثل نظرية الألعاب التطورية والديناميكيات التكيفية، تركيزها على الظواهر الوراثية مثل السيادة، والروكبة، ودرجة كسر إعادة التركيب الجيني لاختلال التناسب الارتباطي بالإضافة إلى الظواهر العشوائية للطفرة والانحراف الوراثي. يجعلها هذا مناسبة للمقارنة مع بيانات الجينوميات الوراثية.
خلفية تاريخية
بدأت الوراثيات السكانية كمصالحة مع الوراثة المندلية ونماذج الإحصاء الحيوي. يمكن للانتخاب الطبيعي أن يتسبب في حدوث تطور إذا كان هناك ما يكفي من التنوع الجينية في مجموعة سكانية ما. وقبل اكتشاف علم الجينات المندلي، كانت الوراثة الخلطية هي الفرضية الشائعة. لكن في حالة الوراثة الخلطية، يضيع التنوع الجيني بسرعة، مما يجعل التطور بالانتخاب الطبيعي أو الجنسي غير محتملا. يقدم مبدأ هاردي-واينبرغ الإجابة عن الكيفية التي يُحفظ بها التنوع في مجموعة سكانية بواسطة الوراثة المندلية. ووفقا لهذا المبدأ، فإن تواترات الأليلات (التنوع في جين ما) سيبقى ثابتا في غياب الانتخاب، الطفرات، الهجرة، والانجراف الوراثي.[3]
كانت الخطوة الهامة التالية هي أعمال البيولوجي والإحصائي البريطاني رونالد فيشر. ففي سلسلة من الأوراق البحثية التي بدأت في عام 1918 وبلغت ذروتها في كتابه لعام 1930 «النظرية الجينية للانتخاب الطبيعي»، أظهر فيشر أن التنوع المستمر المقاس بواسطة مختصي القياسات البيولوجية قد يكون ناجما عن تجمع لأنشطة جينات متقطعة، وأن الانتخاب الطبيعي قد يغير من تواتر الأليلات في تجمع سكاني، ويتسبب بذلك في حدوث تطور. وفي سلسلة من الأوراق البحثية التي بدأت في عام 1924، من قبل عالم جينات بريطاني آخر، جي بي إس هالدين، تم إجراء حسابات تغير تواتر الأليلات في موقع جيني واحد في نطاق عريض من الحالات. كما طبق هالدين أيضا تحليلات إحصائية لأمثلة واقعية من العالم على الانتخاب الطبيعي، كتطور العثة المفلفلة، واسوداد الجلد بفعل الصناعة، وأظهر أن معاملات الانتخاب قد تكون أكبر مما افترض فيشر، ما قاد إلى تطور أسرع تكيفا كاستراتيجية تمويه تبعت ازديد التلوث.[4][5]
ركز البيولوجي الأمريكي سيوال رايت، الذي كانت له خلفية عن تجارب تناسل الحيوانات، على تراكبات الجينات المتداخلة، وتأثيرات التوالد الداخلي على التجمعات الحيوية الصغيرة والمنعزلة نسبيا، والتي خضعت لانجراف جينيا. وفي عام 1932، قدم رايت مفهوم مخططات التكيف، وجادل بأن الانجراف الجيني والتوالد الداخلي قد يدفعان فرعا سكانيا بعيدا عن القمة التكيفية، مما يسمح للانتخاب الطبيعي بدفعه نحو قمم تكيفية أخرى.[بحاجة لمصدر]
أسست أعمال فيشر، هالدين، ورايت لفرع الوراثيات السكانية. وقد وحد ذلك بين الانتخاب الطبيعي وعلم الجينات المندلي، وهالتي كانت الخطوة الحاسمة الأولى في سبيل تطوير نظرية موحدة عن كيفية عمل التطور.[4][5] كان جون مارينارد سميث تلميذا لدى هالدين، بينما كان دبليو دي هاميلتون متأثرا بشدة بمؤلفات فيشر. أما الأمريكي جورج آر برايس فقد عمل مع هاميلتون وأيضا مع مارينارد سيمث. والأمريكي ريتشارد ليونتن والياباني موتو كيمورا تأثرا بشدة برايت.
الارتباط
في حالة وجود جميع الجينات في وضع توازن ارتباطي، يمكن وضع قيمة متوسطة لتأثير الأليل في الموقع الكروموسومي عبر تجميعة الجينات في المواقع الكروموسومية الأخرى. يختلف الأمر في الواقع، إذ يوجد أليل واحد في حالة اختلال توازن ارتباطي مستمر مع جينات المواقع الكروموسومية الأخرى، خاصة مع الجينات القريبة الواقعة على نفس الكروموسوم. تفكك إعادة التركيب اختلال التوازن الارتباطي هذا ببطء شديد من أجل تجنب الترافق الجيني، الذي من شأنه رفع تواتر أليل في موقع كروموسومي ما إلى مستوى عالٍ بسبب ارتباطه بأليل خاضع للاصطفاء في موقع كروموسومي قريب. يبطئ الارتباط أيضًا معدل التكيف، حتى في التجمعات الجنسية.[6][7][8] ينتج تأثير اختلال التوازن الارتباطي في إبطاء معدل التطور التكيفي عن دمج تأثير هيل-روبرتسون (تأخير في جمع الطفرات المفيدة مع بعضها) والاصطفاء الخلفي (تأخير في فصل الطفرات المفيدة عن الترافق الضار).
يشكل الارتباط مشكلة لنماذج الوراثيات السكانية التي تتعامل مع كل موقع كروموسومي لجين محدد على حدة. مع ذلك، يمكن استغلاله كوسيلة لرصد عمل الاصطفاء الطبيعي عبر المسح الاصطفائي.
في الحالات المتطرفة من التكاثر اللاجنسي، يكون الارتباط تام، ويمكن اشتقاق معادلات الوراثيات السكانية وحلها فيما يتعلق بالموجة المنتقلة لتواترات النمط الجيني إلى جانب مخططات الصلاحية البسيطة.[9] تُعد أغلب الميكروبات، مثل البكتيريا، لا جنسية. تشمل الوراثيات السكانية نظامين متناقضين لتكيفها. عندما يكون ناتج معدل الطفرات المفيدة وحجم المجتمع صغيرين، تتبع الجماعات اللاجنسية «نظام التعاقب» الخاص بديناميكيات تثبيت الأصل، مع معدل تكيف معتمد بشكل كبير على هذا الناتج. عندما يكون الناتج أكبر بكثير، تتبع الجماعات اللاجنسية نظام «الطفرات المتزامنة» مع معدل تكيف أقل اعتماداً على الناتج، ويتميز هذا بالتدخل النسيلي وظهور طفرة مفيدة جديدة قبل تثبيت الطفرة الأخيرة.
التطبيقات
شرح مستويات التنوع الوراثي
تتنبأ النظرية المحايدة بتناسب مستوى تنوع النوكليوتيد في مجموعة سكانية ما مع ناتج حجم التجمع ومعدل الطفرات المحايد. تُعرف حقيقة انخفاض مستويات التنوع الوراثي بشكل كبير بالمقارنة مع أحجام التجمع بمصطلح «مفارقة التباين».[10] بينما اعتُبرت مستويات التنوع الوراثي العالية إحدى الحجج الأصلية الداعمة للنظرية المحايدة، ظهرت مفارقة التباين كإحدى أهم الحجج المستخدمة ضدها.
من الواضح وجود اختلاف كبير في مستويات التنوع الجيني داخل الأنواع كدالة لمعدل إعادة التركيب الجيني المحلي، يعود ذلك إلى كل من الترافق الجيني والاصطفاء الخلفي. تستلزم معظم حلول المفارقة الحالية مستوى معين من الاصطفاء في المواقع المرتبطة.[11] على سبيل المثال، يشير أحد التحليلات إلى وجود عمليات مسح اصطفائي أكبر لدى التجمعات الكبيرة، ما يزيل التنوع الوراثي الأكثر حيادية.[12] قد يساهم أيضًا الارتباط السلبي ما بين معدل الطفرات وحجم التجمع.[13]
يؤثر تاريخ الحياة على التنوع الوراثي أكثر من تاريخ التجمع، على سبيل المثال تمتلك استراتيجيات «آر» مقدارًا أكبر من التنوع الوراثي.[11]
رصد الاصطفاء
تُستخدم نماذج الوراثيات السكانية في استنتاج الجينات الخاضعة للاصطفاء. يُعتبر البحث عن المناطق ذات اختلال التوازن الارتباطي العالي والتنوع الوراثي المنخفض على طول الكروموسوم نهجًا شائعًا لرصد المسح الاصطفائي الأخير.
يوجد نهج شائع آخر يُطلق عليه اختبار ماكدونالد-كريتمان. يقارن هذا الاختبار بين كمية التنوع داخل الأنواع (تعدد الأشكال) والتباعد بين الأنواع (الاستبدالات) في نوعين من المواقع التي يُعتبر أحدها محايد.[14] بشكل نموذجي، يُفترض أن مواقع الاستبدال الترادفي محايدة. تمتلك الجينات الخاضعة للاصطفاء الإيجابي فائضًا من مواقع التباعد بالنسبة إلى للمواقع متعددة الأشكال. يمكن استخدام الاختبار أيضًا بهدف إيجاد تقدير على مستوى الجينوم لنسبة الاستبدالات التي أصلحها الاصطفاء الإيجابي ألفا، α.[15][16] وفقًا لنظرية التطور الجزيئي المحايدة، يجب وصول هذا الرقم إلى حدود الصفر تقريبًا. بالتالي، فُسرت الأرقام الكبيرة بوصفها تحريفًا على مستوى الجينوم للنظرية المحايدة.[17]
الاستدلال الديموغرافي
يتمثل الاختبار الأبسط للبنية السكانية، لدى الأنواع ثنائية الصبغيات المتكاثرة جنسيًا، في معرفة ما إذا كانت تواترات النمط الوراثي موافقة لتناسب هاردي-واينبيرغ كدالة لتواترات الأليل. على سبيل المثال، في أبسط حالة للموقع الكروموسومي المفرد مع أليلين يُرمز لهما A وa عند تواتري p «بّي» وq «كيو»، يتنبأ التزاوج العشوائي من أجل AA متماثل الزيجوت، و من أجل aa متماثل الزيجوت و من أجل مغاير الزيجوت. لدى غياب البنية السكانية، يتحقق تناسب هاردي-واينبيرغ خلال جيل إلى جيلين من التزاوج العشوائي. بشكل نموذجي، يوجد زيادة في الأنواع متماثلة الزيجوت ما يدل على البنية السكانية. يمكن قياس كمية هذه الزيادة كمعامل زواج الأقارب، «إف».
يمكن تجميع الأفراد في المجموعات السكانية الفرعية «كيه».[18][19] يمكن عندئذ قياس درجة البنية السكانية باستخدام مؤشر التثبيت FST، وهو مقياس لتناسب التنوع الوراثي الذي تفسره البنية الوراثية. تُربط البنية السكانية الوراثية بعد ذلك مع البنية الجغرافية، ثم يصبح بالإمكان رصد الخلط الوراثي.
تربط نظرية الاندماج عينة من التنوع الوراثي بالتاريخ الديمغرافي للمجموعة السكانية التي اشتُق منها. تفترض عادةً الحيادية، ما يؤدي إلى اختيار الأجزاء المتطورة الأكثر حيادية من الجينوم لمثل هذا التحليل. يمكن استخدام هذه النظرية بهدف استنتاج العلاقات بين الأنواع (علم الوراثة العرقي الحسابي)، بالإضافة إلى البنية السكانية، والتاريخ الديمغرافي (على سبيل المثال، عنق الزجاجة السكانية والنمو السكاني)، والانتشار الحيوي، وديناميكيات الموائل عالية-رديئة الجودة[20] والانجبال الداخلي بين الأنواع.
يعتمد عدد من الطرق الأخرى للاستدلال الديمغرافي على طيف تواتر الأليل.[21]
تطور الأنظمة الوراثية
عبر افتراض وجود موقع كروموسومي متحكم في النظام الوراثي نفسه، تُصنع النماذج الوراثية السكانية من أجل وصف تطور السيادة وغيرها من أشكال القوة، وتطور التكاثر الجنسي ومعدلات التهجين، وتطور معدل الطفرات، وتطور السعات التطورية، وتطور صفات الإشارات المكلفة، وتطور الشيخوخة وتطور التعاون. على سبيل المثال، تُعد معظم الطفرات ضارة، لذا يُحسب معدل الطفرات الأمثل للأنواع من خلال الموازنة بين التلف الناجم عن معدل الطفرات شديد الضرر والتكاليف الاستقلابية المحافظة على الأنظمة التي من شأنها تقليص معدل الطفرات، مثل إنزيمات إصلاح الدنا.[22]
تتمثل إحدى الجوانب المهمة لمثل هذه النماذج في قدرة الاصطفاء على إزالة الطفرات الضارة، ما يؤدي إلى التغلب على تحيز الطفرات نحو التدهور في حال كان معامل الاصطفاء «إس» أكبر من مقلوب حجم التجمع الفعال. يُعرف هذا بحاجز الانحراف ويرتبط مع نظرية التطور الجزيئي شبه المحايدة. تتنبأ نظرية حاجز الانحراف بامتلاك أحجام التجمع الفعال الكبيرة أنظمة وراثية فعالة عالية التنظيم، بينما تمتلك أحجام التجمع الصغيرة جينومات متضخمة ومعقدة حاوية، على سبيل المثال، على الإنترونات والجينات القافزة.[23] مع ذلك، وبشكل متناقض إلى حد ما، قد تكون الأنواع ذات أحجام التجمع الفعال الكبيرة متساهلة بشكل أكبر مع عواقب أنواع معينة من الأخطاء مسببة تطور معدلات أخطاء أعلى، كما في النسخ والترجمة مثلا، بالمقارنة مع التجمعات الصغيرة.[24]
مراجع
- "Population genetics - Latest research and news"، www.nature.com، مؤرشف من الأصل في 16 يناير 2021، اطلع عليه بتاريخ 29 يناير 2018.
- Servedio, Maria R.؛ Brandvain, Yaniv؛ Dhole, Sumit؛ Fitzpatrick, Courtney L.؛ Goldberg, Emma E.؛ Stern, Caitlin A.؛ Van Cleve, Jeremy؛ Yeh, D. Justin (09 ديسمبر 2014)، "Not Just a Theory—The Utility of Mathematical Models in Evolutionary Biology"، PLOS Biology، 12 (12): e1002017، doi:10.1371/journal.pbio.1002017، PMC 4260780، PMID 25489940.
- Ewens W.J. (2004)، Mathematical Population Genetics (2nd Edition)، Springer-Verlag, New York، ISBN 978-0-387-20191-7.
- Bowler, Peter J. (2003)، Evolution : the history of an idea (ط. 3rd)، Berkeley: University of California Press، ص. 325–339، ISBN 978-0-520-23693-6، مؤرشف من الأصل في 27 فبراير 2021.
- Larson, Edward J. (2004)، Evolution : the remarkable history of a scientific theory (ط. Modern Library)، New York: Modern Library، ص. 221–243، ISBN 978-0-679-64288-6، مؤرشف من الأصل في 16 ديسمبر 2019.
- Weissman, D. B.؛ Hallatschek, O. (15 يناير 2014)، "The Rate of Adaptation in Large Sexual Populations with Linear Chromosomes"، Genetics، 196 (4): 1167–1183، doi:10.1534/genetics.113.160705، PMC 3982688، PMID 24429280.
- Weissman, Daniel B.؛ Barton, Nicholas H.؛ McVean, Gil (07 يونيو 2012)، "Limits to the Rate of Adaptive Substitution in Sexual Populations"، PLOS Genetics، 8 (6): e1002740، doi:10.1371/journal.pgen.1002740، PMC 3369949، PMID 22685419.
- Neher, R. A.؛ Shraiman, B. I.؛ Fisher, D. S. (30 نوفمبر 2009)، "Rate of Adaptation in Large Sexual Populations"، Genetics، 184 (2): 467–481، arXiv:1108.3464، doi:10.1534/genetics.109.109009، PMC 2828726، PMID 19948891.
- Desai, Michael M.؛ Fisher, Daniel S. (2007)، "Beneficial Mutation Selection Balance and the Effect of Linkage on Positive Selection"، Genetics، 176 (3): 1759–1798، doi:10.1534/genetics.106.067678، PMC 1931526، PMID 17483432.
- Lewontin, R. C. (1973)، The genetic basis of evolutionary change (ط. [4th printing.])، New York: Columbia University Press، ISBN 978-0231033923، مؤرشف من الأصل في 17 أغسطس 2021.
- Ellegren, Hans؛ Galtier, Nicolas (06 يونيو 2016)، "Determinants of genetic diversity"، Nature Reviews Genetics، 17 (7): 422–433، doi:10.1038/nrg.2016.58، PMID 27265362، S2CID 23531428، مؤرشف من الأصل في 08 نوفمبر 2020.
- Corbett-Detig, Russell B.؛ Hartl, Daniel L.؛ Sackton, Timothy B.؛ Barton, Nick H. (10 أبريل 2015)، "Natural Selection Constrains Neutral Diversity across A Wide Range of Species"، PLOS Biology، 13 (4): e1002112، doi:10.1371/journal.pbio.1002112، PMC 4393120، PMID 25859758.
- Sung, W.؛ Ackerman, M. S.؛ Miller, S. F.؛ Doak, T. G.؛ Lynch, M. (17 أكتوبر 2012)، "Drift-barrier hypothesis and mutation-rate evolution" (PDF)، Proceedings of the National Academy of Sciences، 109 (45): 18488–18492، Bibcode:2012PNAS..10918488S، doi:10.1073/pnas.1216223109، PMC 3494944، PMID 23077252، مؤرشف من الأصل (PDF) في 15 فبراير 2020.
- Charlesworth, J. Eyre-Walker (2008)، "The McDonald–Kreitman Test and Slightly Deleterious Mutations"، Molecular Biology and Evolution، 25 (6): 1007–1015، doi:10.1093/molbev/msn005، PMID 18195052.
- Eyre-Walker, A. (2006)، "The genomic rate of adaptive evolution" (PDF)، Trends in Ecology and Evolution، 21 (10): 569–575، doi:10.1016/j.tree.2006.06.015، PMID 16820244، مؤرشف من الأصل (PDF) في 20 مارس 2016.
- Smith, N. G. C.؛ Eyre-Walker, A. (2002)، "Adaptive protein evolution in Drosophila"، Nature، 415 (6875): 1022–1024، Bibcode:2002Natur.415.1022S، doi:10.1038/4151022a، PMID 11875568، S2CID 4426258.
- Hahn, M. W. (2008)، "Toward a selection theory of molecular evolution"، Evolution، 62 (2): 255–265، doi:10.1111/j.1558-5646.2007.00308.x، PMID 18302709، S2CID 5986211.
- Pritchard, J. K.؛ Stephens, M.؛ Donnelly, P. (يونيو 2000)، "Inference of population structure using multilocus genotype data"، Genetics، 155 (2): 945–959، ISSN 0016-6731، PMC 1461096، PMID 10835412.
- Verity, Robert؛ Nichols, Richard A. (أغسطس 2016)، "Estimating the Number of Subpopulations (K) in Structured Populations"، Genetics، 203 (4): 1827–1839، doi:10.1534/genetics.115.180992، ISSN 0016-6731، PMC 4981280، PMID 27317680.
- Manlik, Oliver؛ Chabanne, Delphine؛ Daniel, Claire؛ Bejder, Lars؛ Allen, Simon J.؛ Sherwin, William B. (13 نوفمبر 2018)، "Demography and genetics suggest reversal of dolphin source–sink dynamics, with implications for conservation."، Marine Mammal Science، 35 (3): 732–759، doi:10.1111/mms.12555.
- Gutenkunst, Ryan N.؛ Hernandez, Ryan D.؛ Williamson, Scott H.؛ Bustamante, Carlos D.؛ McVean, Gil (23 أكتوبر 2009)، "Inferring the Joint Demographic History of Multiple Populations from Multidimensional SNP Frequency Data"، PLOS Genetics، 5 (10): e1000695، arXiv:0909.0925، doi:10.1371/journal.pgen.1000695، PMC 2760211، PMID 19851460.
- Sniegowski, P. (2000)، Gerrish P.; Johnson T;. Shaver A.، "The evolution of mutation rates: separating causes from consequences"، BioEssays، 22 (12): 1057–1066، doi:10.1002/1521-1878(200012)22:12<1057::AID-BIES3>3.0.CO;2-W، PMID 11084621.
- Lynch, Michael؛ Conery, John S. (2003)، "The origins of genome complexity"، ساينس، 302 (5649): 1401–1404، Bibcode:2003Sci...302.1401L، CiteSeerX 10.1.1.135.974، doi:10.1126/science.1089370، PMID 14631042، S2CID 11246091.
- Rajon, E.؛ Masel, J. (03 يناير 2011)، "Evolution of molecular error rates and the consequences for evolvability"، Proceedings of the National Academy of Sciences، 108 (3): 1082–1087، Bibcode:2011PNAS..108.1082R، doi:10.1073/pnas.1012918108، PMC 3024668، PMID 21199946.
- بوابة علم الأحياء
- بوابة علم الأحياء الخلوي والجزيئي
- بوابة علم الأحياء التطوري
