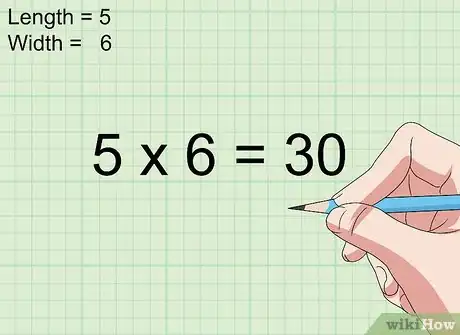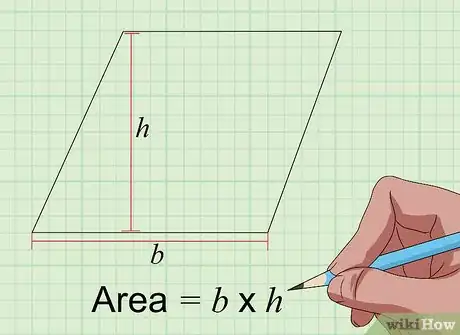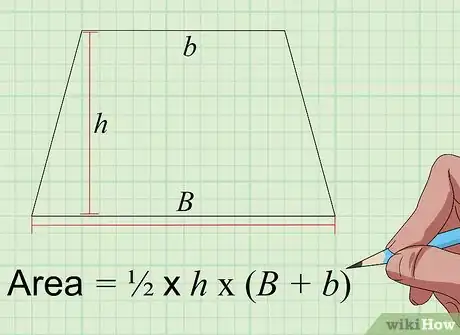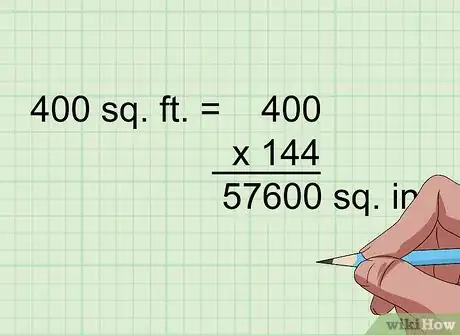Cómo calcular los centímetros cuadrados

Coescrito por David Jia

Determinar los centímetros cuadrados (también escritos "cm²") de cualquier superficie bidimensional suele ser un proceso bastante directo. En los casos más sencillos, cuando la superficie en cuestión tiene forma de cuadrado o rectángulo, su área en centímetros cuadrados viene dada por la ecuación ancho × longitud. El área de otras figuras planas (círculos, triángulos, etc.) se puede calcular mediante una serie de ecuaciones matemáticas específicas. También puedes hacer conversiones simples de pulgadas o pies cuadrados a centímetros cuadrados, si es necesario.

Método 1

Método 1 de 3:
Determinar los centímetros cuadrados de un cuadrado o un rectángulo

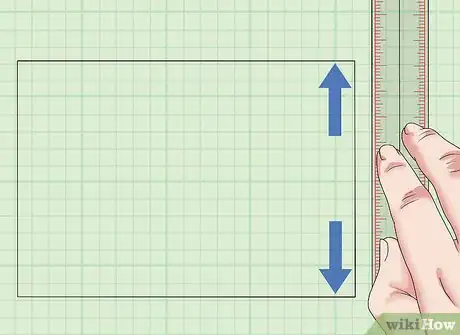
1
Determina la longitud de la superficie a medir. Los cuadrados y los rectángulos tienen cuatro lados rectos. En el caso de los rectángulos, los lados opuestos tienen la misma longitud, mientras que en los cuadrados, todos los lados son iguales. Mide cualquier lado del cuadrado o del rectángulo para hallar el valor de la longitud.^{[1]
X
Fuente de investigación}
2
Determina el ancho de la superficie a medir. A continuación, mide cualquiera de los dos lados que esté en contacto con el lado cuya longitud acabas de hallar. Este lado debe encontrarse con el primer lado formando un ángulo de 90 grados. Esta segunda medida es el ancho del cuadrado o el rectángulo.^{[2]
X
Fuente de investigación}
- Dado que todos los lados de un cuadrado son iguales, la medida que resulte para su longitud será idéntica a la de su ancho. En tal caso, solo tendrás que medir un lado.
3
Multiplica longitud × ancho. Simplemente multiplica las medidas de la longitud y el ancho para determinar el área de la superficie cuadrada o rectangular en centímetros cuadrados.^{[3]
X
Fuente de investigación}
- Por ejemplo, supongamos que mides una superficie rectangular de longitud igual a 4 centímetros y ancho igual a 3 centímetros. En tal caso, el área del rectángulo es 4 × 3 = 12 centímetros cuadrados.
- En el caso de los cuadrados, dado que sus cuatro lados son iguales, solo tendrás que conseguir la medida de un lado y multiplicarla por sí misma (proceso que también se conoce como "elevar al cuadrado" o "elevar a la segunda potencia") para hallar el valor del área en centímetros cuadrados.
Anuncio

Método 2

Método 2 de 3:
Determinar los centímetros cuadrados de otras figuras

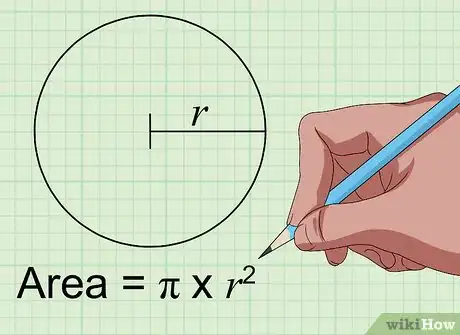
1
Halla el área de un círculo con la ecuación "área = pi × r²". Para calcular el área de un círculo en centímetros cuadrados, solo necesitas conocer la distancia que hay desde el centro de dicho círculo hasta el contorno dado en centímetros cuadrados. Esta distancia se llama "radio". Una vez que hayas hallado este valor, solo tendrás que introducirlo en el lugar de la "r" de la ecuación anterior. Multiplícalo por sí mismo y, después, por la constante matemática "pi" (3,1415926...) para determinar cuántos centímetros cuadrados mide la superficie del círculo.^{[4]
X
Fuente de investigación}
- Por lo tanto, un círculo cuyo radio mida 4 centímetros tendrá un área de 50,27 centímetros cuadrados, ya que este es el producto de la multiplicación 3,14 × 16.
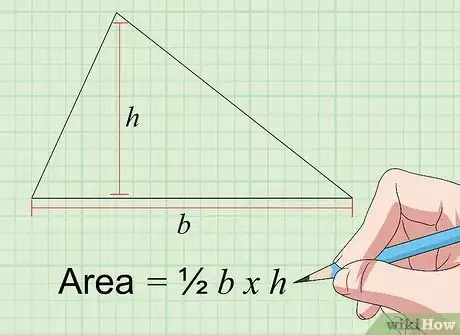
2
Halla el área de un triángulo con la ecuación "área = 1/2 b × h". El área de un triángulo en centímetros cuadrados se calcula multiplicando su base ("b") por su altura ("h"), con ambas medidas expresadas en centímetros. La base de un triángulo es simplemente la longitud de uno de sus lados, mientras que su altura es la distancia que hay desde el lado de base hasta el vértice opuesto, medida mediante un segmento perpendicular al primero. El área de un triángulo se puede calcular utilizando las medidas de la base y la altura correspondientes a cualquiera de sus lados y el vértice opuesto.^{[5]
X
Fuente de investigación}
- Por lo tanto, si eliges un lado de base de longitud igual a 4 centímetros y su altura correspondientes es de 3 centímetros, el resultado será: 2 × 3 = 6 centímetros cuadrados.
3
Halla el área de un paralelogramo con la ecuación "área = b × h". Los paralelogramos son parecidos a los rectángulos, con la diferencia de que sus esquinas no tienen por qué formar ángulos de 90 grados. La manera adecuada de calcular el área de un paralelogramo en centímetros cuadrados es parecida a la forma de calcular el área de un rectángulo. Solo tienes que multiplicar una base del paralelogramo por su altura, con ambas medidas dadas en centímetros. Su base es la longitud de uno de sus lados, mientras que la altura es la distancia que hay desde el lado opuesto al primer lado, medida en ángulo recto.^{[6]
X
Fuente de investigación}
- Es decir, si la longitud de un lado determinado es de 5 centímetros y su altura correspondiente es de 4 centímetros, el área resultante será: 5 × 4 = 20 centímetros cuadrados.
4
Halla el área de un trapezoide con la ecuación "área = 1/2 × h × (B+b)". Un trapezoide es una figura de cuatro lados con un par de lados paralelos entre sí y otro par de lados no paralelos entre sí. Para calcular su área en centímetros cuadrados, deberás tomar tres medidas (en centímetros): la longitud del lado paralelo más largo ("B"), la longitud del lado paralelo más corto ("b") y la altura del trapezoide ("h"), que es la distancia medida en ángulo recto entre los dos lados paralelos. Suma las longitudes de los dos lados, multiplica el resultado por la altura y, después, divide el resultado por la mitad para hallar el área del trapezoide en centímetros cuadrados.^{[7]
X
Fuente de investigación}
- Por lo tanto, si el lado más largo del trapezoide mide 6 centímetros, el lado más corto mide 4 centímetros y su altura es de 5 centímetros, el resultado es: ½ × 5 × (6+4) = 25 centímetros cuadrados.
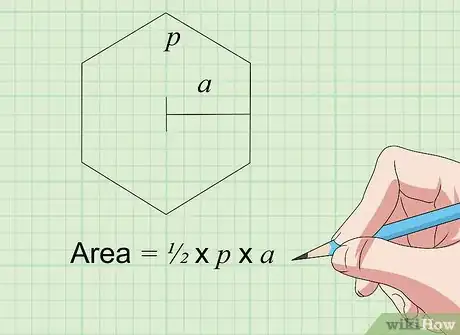
5
Calcula el área de un hexágono con la ecuación "área = ½ × P × a". Esta fórmula funciona con cualquier hexágono regular, que es una figura plana de seis lados iguales y seis ángulos iguales. P representa el perímetro, equivalente a la longitud de un lado multiplicada por 6 (6 × s) en el caso de un hexágono regular. a representa la apotema, que es la longitud que hay desde el centro del hexágono al punto medio de cualquiera de sus lados (es decir, a medio camino entre dos vértices contiguos cualesquiera). Haz esta multiplicación y anota el resultado para determinar el área.^{[8]
X
Fuente de investigación}
- Por lo tanto, si el hexágono tiene 6 lados iguales de 4 centímetros cada uno (lo cual se resume en "P = 6 × 4 = 24") y su apotema es de 3,5 centímetros, la operación para hallar el área es: ½ × 24 × 3,5 = 42 centímetros cuadrados.
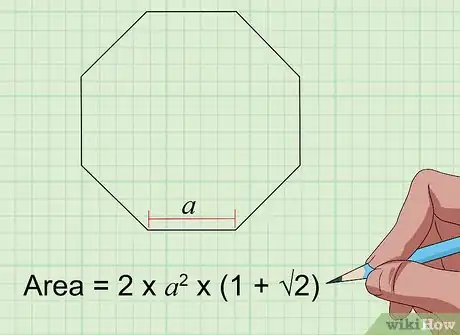
6
Calcula el área de un octágono con la ecuación "área = 2a² × (1 + √2)". En el caso de un octágono regular (con ocho lados iguales y ocho ángulos iguales), solo necesitarás conocer la longitud de un lado (“a” en la fórmula) para determinar su área. Introduce ese valor en la fórmula y te dará el resultado.^{[9]
X
Fuente de investigación}
- Por lo tanto, si la longitud del lado del octágono regular es de 4 centímetros, la operación será: 2(16) × (1 + 1,4) = 32 × 2,4 = 76,8 centímetros cuadrados.
Anuncio

Método 3

Método 3 de 3:
Hacer conversiones a centímetros cuadrados

1
Convierte las medidas a centímetros antes de hacer las operaciones. Para que te dé el resultado final en centímetros cuadrados, es más sencillo utilizar todas las medidas requeridas para la fórmula (como longitud, altura y apotema) en centímetros. Por lo tanto, si cada lado del cuadrado mide 1 pie, deberás convertir esta medida a 30,48 cm antes de calcular el área. Aquí tienes unos cuantos factores de conversión para las unidades de medida más comunes:
- 1 pie = 30,48 cm
- 1 yarda = 91,44 cm
- 1 pulgada = 2,54 cm
- 1 metro = 100 cm
- 1 milímetro = 0,1 cm
2
Multiplica por 929,03 para convertir pies cuadrados en centímetros cuadrados. 1 pie cuadrado es literalmente 1 pie al cuadrado (o, lo que es lo mismo, 1 pie por 1 pie). Esto quiere decir que equivale a 30,48 centímetros multiplicados por 30,48 centímetros, o 929,03 centímetros. Por lo tanto, si tienes un área dada en pies cuadrados, solo tienes que multiplicarla por 929,03 para determinar el valor en centímetros cuadrados.^{[10]
X
Fuente de investigación}
- Por ejemplo, 400 pies cuadrados = 400 x 929,03 = 371 612
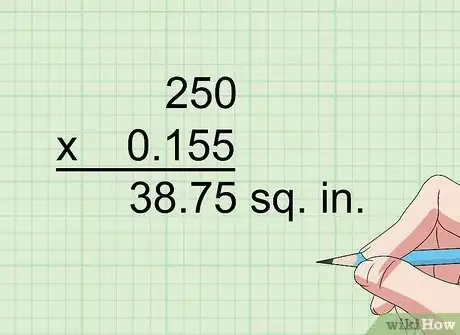
3
Multiplica por 6,45 para convertir pulgadas cuadradas en centímetros cuadrados. 1 pulgadas equivale, aproximadamente, a 2,54 centímetros, y 2,54 elevado al cuadrado (2,54 x 2,54) es igual a 6,45. Por lo tanto, si tienes que convertir un resultado de 250 pulgadas, multiplica 250 por 6,45 para que te dé 1612,5 centímetros cuadrados.^{[11]
X
Fuente de investigación}
- Además, 1 metro cuadrado es igual a 10 000 centímetros cuadrados, y un kilómetro cuadrado es igual a 10 000 000 000 centímetros cuadrados.
Anuncio