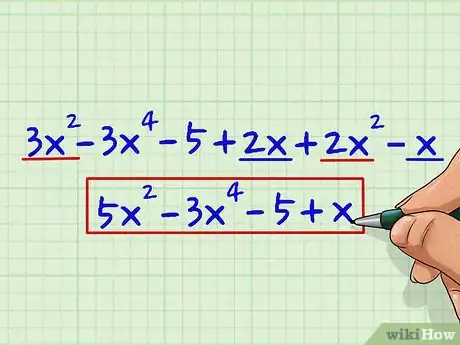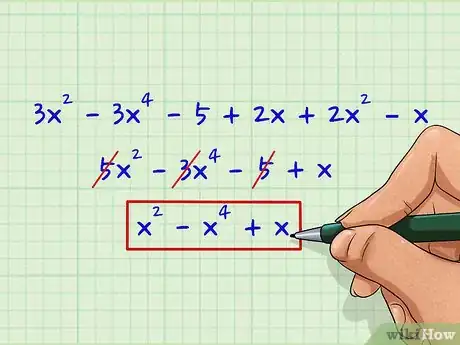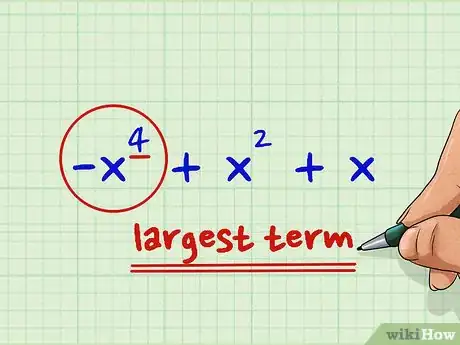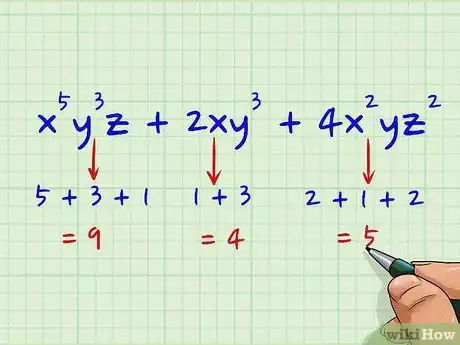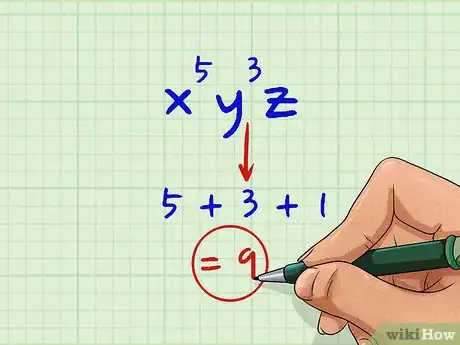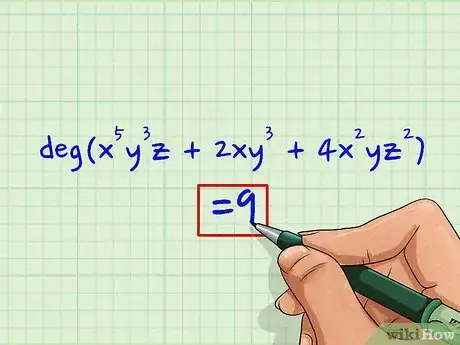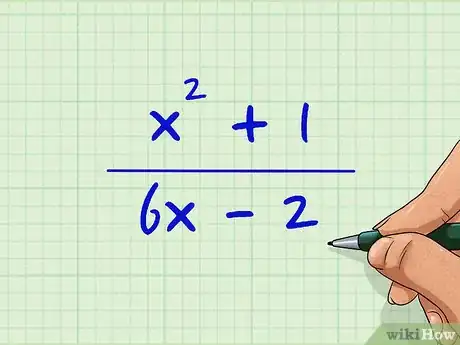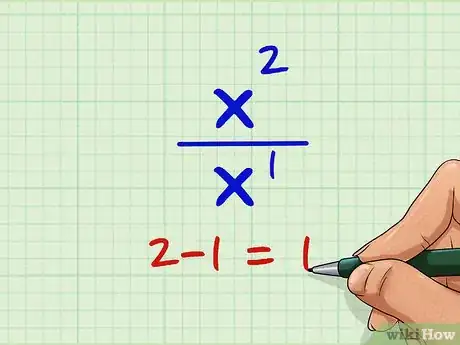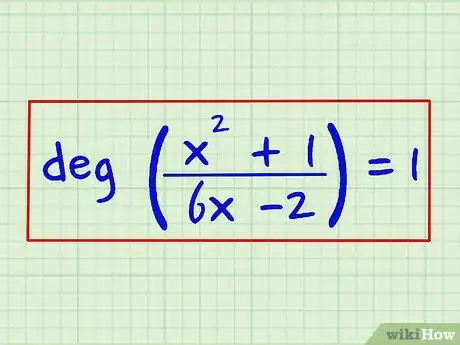Cómo encontrar el grado de un polinomio

Información del autor

Polinomio significa "muchos términos" y puede hacer referencia a una gran variedad de expresiones con constantes, variables y exponentes. Por ejemplo, x – 2 es un polinomio. 25 también lo es. Para encontrar el grado de un polinomio, lo único que tienes que hacer es determinar cuál es el exponente más grande.^{[1]
X
Fuente de investigación} Sigue estos pasos si quieres aprender a encontrar el grado de un polinomio en diversas situaciones.

Parte 1

Parte 1 de 3:
Polinomios de una variable o menos

1
Combina los términos semejantes. Combina todos los términos semejantes de la expresión para poder simplificarla (si es que no lo están). Imagina que tienes que trabajar con la siguiente expresión: 3x² - 3x⁴ - 5 + 2x + 2x² - x. Combina todas las x², x y términos constantes de la expresión para obtener 5x² - 3x⁴ - 5 + x.
2
Deshazte de todas las constantes y coeficientes. Los términos constantes son todos aquellos que no están unidos a ninguna variable, por ejemplo 3 o 5. Los coeficientes son aquellos términos que están unidos a una variable. Si quieres encontrar el grado de un polinomio, puedes simplemente ignorar estos términos o bien tacharlos. Por ejemplo, el coeficiente del término 5x² es 5. El grado no depende de los coeficientes, por eso no los necesitas.
- Si, por ejemplo, eliminas las constantes y coeficientes de la ecuación 5x² - 3x⁴ - 5 + x, obtendrás x² - x⁴ + x.
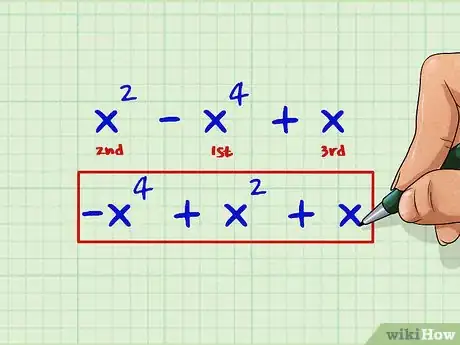
3
Escribe los términos en orden decreciente según sus exponentes. Esto es lo que se conoce como "forma estándar" de expresar un polinomio.^{[2]
X
Fuente de investigación} El término que tenga el exponente más alto debe ir primero y el que tenga el más bajo debe ir al final. Esto te ayudará a ver cuál es el término que tiene el exponente de mayor valor. El polinomio del ejemplo anterior quedaría así:
-x⁴ + x² + x.
4
Busca la potencia del término más grande. La potencia es simplemente el número que aparece en el exponente. En el ejemplo de -x⁴ + x² + x, la potencia del primer término es 4. Como habías ordenado el polinomio ubicando el exponente más grande en primer lugar, ahí es donde debes buscar la mayor potencia.
5
Identifica este número como el grado del polinomio. Puedes simplemente escribir que el grado del polinomio es igual a 4, o bien expresar la respuesta en la forma apropiada: grado(3x² - 3x⁴ - 5 + 2x + 2x² - x)=4. Eso es todo.^{[3]
X
Fuente de investigación}
6
Ten presente que el grado de una constante es cero. Si tu polinomio es solo una constante como 15 o 55, entonces el grado de ese polinomio es cero. Puedes pensar en el término constante como un término unido a una variable de grado 0, que en realidad es 1. Por ejemplo, si tienes la constante 15, puedes verla como 15x⁰, que es lo mismo que 15 x 1 o simplemente 15. Esto demuestra que el grado de una constante es siempre 0.

Parte 2

Parte 2 de 3:
Polinomios de muchas variables

1
Escribe la expresión. Encontrar el grado de un polinomio de muchas variables es apenas un poco más difícil que el de una variable. Imagina que tienes que trabajar con la siguiente expresión:
- x⁵y³z + 2xy³ + 4x²yz²
2
Suma el grado de las variables de cada término. Simplemente suma el grado de las variables de cada uno de los términos. No importa que las variables sean diferentes. Recuerda que, si el grado de una variable no está expresado explícitamente, por ejemplo, en el caso de x o y, entonces es igual a uno. A continuación verás cómo hacerlo para los tres términos de la expresión anterior:^{[4]
X
Fuente de investigación}
- grado(x⁵y³z) = 5 + 3 + 1 = 9
- grado(2xy³) = 1 + 3 = 4
- grado(4x²yz²) = 2 + 1 + 2 = 5
3
Identifica al mayor de los tres términos. El grado más alto de los tres términos es 9, que es el valor que se obtiene al sumar los tres grados del primer término.
4
Identifica este número como grado del polinomio. El grado del polinomio completo es 9. Puedes escribir la respuesta final de la siguiente manera: grado(x⁵y³z + 2xy³ + 4x²yz²)=9.

Parte 3

Parte 3 de 3:
Expresiones racionales

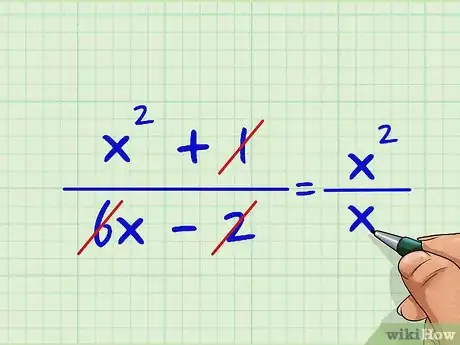
1
Anota la expresión. Imagina que tienes que trabajar con la siguiente expresión:(x² + 1)/(6x -2).^{[5]
X
Fuente de investigación}
2
Elimina todos los coeficientes y las constantes. Los coeficientes y las constantes no son necesarios para encontrar el grado de un polinomio con fracciones. Por este motivo, puedes eliminar el 1 del numerador y el 6 y el -2 del denominador. Te quedará x²/x.
3
Réstale el grado de la variable del denominador al grado del numerador. El grado de la variable del numerador es 2 y el grado de la variable del denominador es 1. Por lo tanto, tienes que restarle 1 a 2. 2 - 1 = 1.
4
Escribe el resultado como respuesta. El grado de la esta expresión racional es 1. Puedes reescribirlo de la siguiente manera: grado [(x² + 1)/(6x -2)] = 1.

Consejos

Estos pasos se pueden realizar mentalmente. No es necesario que lo escribas en papel, aunque podría resultarte de gran ayuda si es la primera vez que lo haces. De esa forma será menos probable que cometas un error.
Por convención, el grado del polinomio cero se considera generalmente como infinitamente negativo.
Para el tercer paso, los términos lineales como x se pueden expresar de la forma x¹ y los términos constantes distintos de cero, por ejemplo, 7, se pueden expresar de la forma 7x⁰.