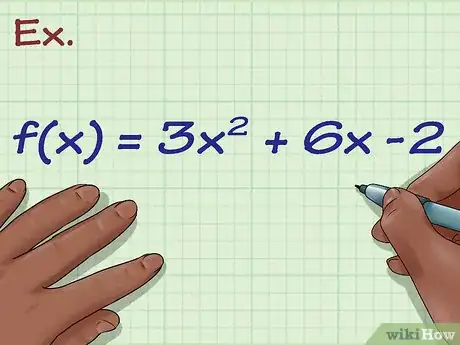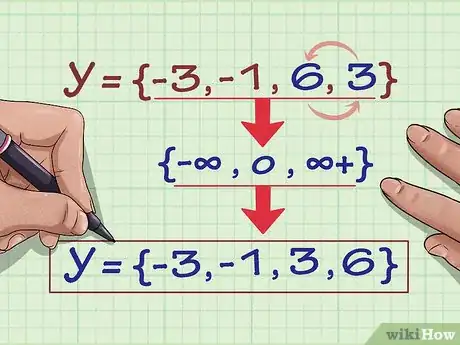X
Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
Este artículo ha sido visto 237 227 veces.
La imagen (o rango) de una función es el conjunto de números que puede generar la función. En otras palabras, es el conjunto de valores de y que obtienes cuando evalúas en la función todos los valores de x posibles. Este conjunto de los valores de x posibles se llama dominio. Si quieres saber cómo encontrar la imagen de una función, simplemente sigue estos pasos.
Pasos
Método 1
Método 1 de 4:Encuentra la imagen de una función con una fórmula dada
Método 1
-
1Anota la fórmula. Digamos que la fórmula con la que trabajas es: f(x) = 3x2 + 6x - 2. Esto significa que cuando reemplaces cualquier valor de x en la ecuación, obtendrás un valor de y. Esta es la función de una parábola.[1]
-
2Encuentra el vértice de la función si es cuadrática. Si trabajas con una recta o con cualquier función polinómica con exponentes impares, como f(x) = 6x3+2x + 7, puedes saltearte este paso. Pero si trabajas con una parábola, o con cualquier ecuación en la cual la variable x esté elevada al cuadrado o a una potencia par, deberás trazar el vértice. Para hacerlo, simplemente utiliza la fórmula -b/2a para obtener la variable x de la función 3x2 + 6x -2, en la cual 3 = a, 6 = b, y -2 = c. En este caso -b es -6, y 2a es 6, así que la variable x es -6/6, o -1.[2]
- Ahora, reemplaza x por -1 en la función para obtener la variable y. f(-1) = 3(-1)2 + 6(-1) -2 = 3 - 6 -2 = -5.
- El vértice es (-1,-5). Grafícalo dibujando un punto donde la variable x es -1 y donde la variable y es -5. Debería estar ubicado en el tercer cuadrante del gráfico.
-
3Encuentra algunos otros puntos de la función. Para tener una idea de la función, reemplaza a la x por algunos otros valores y así obtener una idea de cómo luce la función antes de comenzar a buscar la imagen. Ya que es una parábola y la variable x2 es positiva, estará apuntando hacia arriba. Pero sólo para no dar margen a errores, reemplacemos algunos valores de la variable x para ver los valores de la variable y que estos devuelven:[3]
- f(-2) = 3(-2)2 + 6(-2) -2 = -2. Un punto del gráfico es (-2, -2)
- f(0) = 3(0)2 + 6(0) -2 = -2. Otro punto del gráfico es (0,-2)
- f(1) = 3(1)2 + 6(1) -2 = 7. Un tercer punto del gráfico es (1, 7).
-
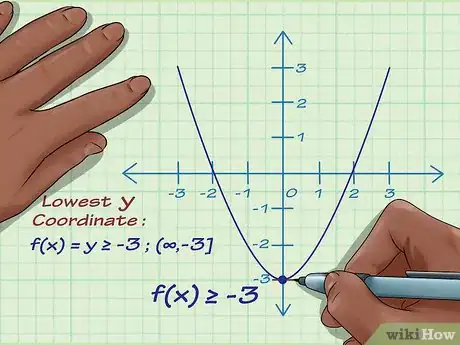
4Encuentra la imagen en el gráfico. Ahora, observa la variable y en el gráfico y encuentra el valor mínimo de la variable y que “toque” el gráfico. En este caso, el valor mínimo de la variable y es el del vértice, -5, y por encima de este punto, el gráfico se extiende hacia arriba infinitamente. Esto quiere decir que la imagen de la función es y = todos los números reales ≥ -5.[4]
Método 2
Método 2 de 4:Encuentra la imagen de una función en un gráfico
Método 2
-
1Encuentra el mínimo de la función. Busca el valor más bajo de la variable y de la función. Supongamos que la función alcanza su mínimo en -3. Esta función también podría hacerse más y más pequeña infinitamente, sin llegar a un valor mínimo determinado, sólo disminuyendo infinitamente.
-
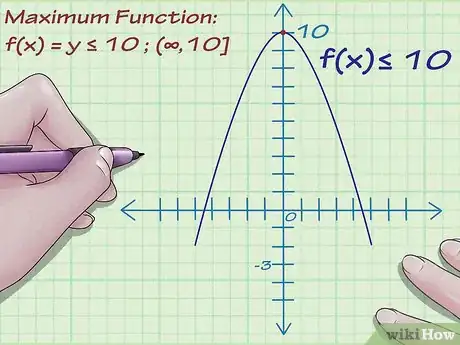
2Encuentra el máximo de la función. Supongamos que el valor más alto que alcanza la variable y en la función es 10. La función también podría hacerse más y más grande infinitamente, sin llegar a un valor máximo determinado, sólo aumentando infinitamente.
-
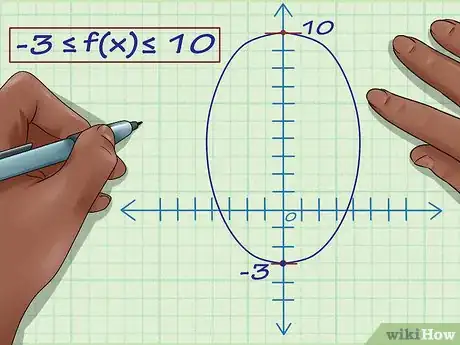
3Determina la imagen. Esto significa que la imagen de la función, o la imagen de la variable y va desde -3 hasta 10. Entonces, -3 ≤ f(x) ≤ 10. Esta es la imagen de la función.
- Pero supongamos que el gráfico alcanza su punto mínimo para y = -3, pero aumenta hasta infinito. Entonces el rango es f(x) ≥ -3, y nada más.
- Supongamos que el gráfico alcanza su punto máximo en 10 pero luego disminuye hasta infinito. Entonces el rango es f(x) ≤ 10.
Método 3
Método 3 de 4:Encuentra la imagen de una función de una relación
Método 3
-
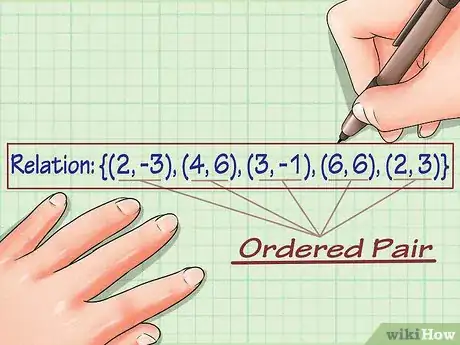
1Anota la relación. Una relación es un conjunto de pares ordenados con variables x e y. Con sólo observar una relación puedes determinar su dominio e imagen. Supongamos que trabajas con la siguiente relación: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.[5]
-
2Haz una lista de las variables y de la relación. Para encontrar el rango de la relación, simplemente anota todos los valores de y para cada par ordenado: {-3, 6, -1, 6, 3}.[6]
-
3Elimina cualquier valor duplicado para obtener así un solo valor para cada y. Puedes notar quue en la lista aparece dos veces el “6”. Quita uno para quedarte con{-3, -1, 6, 3}.[7]
-
4Escriba la imagen de la relación en orden ascendente. Ahora, reordena los números del conjunto de manera que vayan del más pequeño al más grande, y así obtienes la imagen. La imagen de la relación es {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} is {-3,-1, 3, 6}. Ya has terminado.[8]
-
5Asegúrate de que la relación sea una función. Para que una relación sea un función, cada vez que reemplaces x por un valor, el valor que tome la variable y debe ser el mismo. Por ejemplo, la relación {(2, 3) (2, 4) (6, 9)} no es una función, porque cuando reemplazas x por 2 la primera vez, obtienes un 3, pero cuando reemplazas por 2 la segunda vez, obtienes un cuatro. Para que una relación sea función, si reemplazas por el mismo valor de entrada, debes obtener siempre el mismo valor de salida. Si pones un -7, debes obtener el mismo valor de la variable y (sea el valor que sea) todas y cada una de las veces.[9]
Método 4
Método 4 de 4:Encuentra la imagen de una función en un problema enunciado
Método 4
-
1Lee el problema. Supongamos que trabajas con el siguiente problema: "Beatriz está vendiendo entradas para el espectáculo de talentos de su escuela a 5 dólares cada una. La cantidad de dinero que reúna es función de la cuántas entradas venda. ¿Cuál es la imagen de la función?” .
-
2Escribe el problema como una función. En este caso, M representa la cantidad de dinero que ella reúne, y t representa la cantidad de entradas que venda. Sin embargo, ya que cada entrada costará 5 dólares, debes multiplicar la cantidad de entradas vendidas por 5 para encontrar la cantidad de dinero. Entonces, la función puede escribirse como M(t) = 5t.
- Por ejemplo, si ella vende 2 entradas, deberás multiplicar 2 por 5 para obtener 10, la cantidad de dólares que ella reunirá.
-
3Determina el dominio. Para determinar la imagen, primero debes encontrar el dominio. El dominio son todos los valores posibles de t que puedan tomar la ecuación. En este caso, Beatriz puede vender 0 o más entradas, pero no puede vender entradas negativas. Ya que no conocemos la cantidad de asientos en el auditorio de su escuela, podemos asumir que teóricamente puede vender una cantidad infinita de entradas. Y únicamente puede vender una cantidad entera de entradas; no puede vender 1/2 entrada, por ejemplo. Por lo tanto, el dominio de la función es t = cualquier número entero positivo.
-
4Determina la imagen. La imagen es la cantidad de dinero posible que Beatriz puede obtener con su venta. Tienes que trabajar con el dominio para encontrar la imagen. Si sabes que el dominio es cualquier número entero positivo y que la función es M(t) = 5t, entonces sabes que puedes reemplazar t por cualquier número entero positivo en la función para obtener la salida, o la imagen. Por ejemplo, si ella vende 5 entradas, entonces M(5) = 5 x 5, o 25 dólares. Si ella vende 100, entonces M(100) = 5 x 100, o 500 dólares. Por lo tanto, la imagen de la función es cualquier número entero positivo que sea múltiplo de cinco.
- Eso significa que cualquier número entero positivo que sea múltiplo de cinco es una salida posible para la entrada de la función.
Consejos
- Fíjate si puedes encontrar la inversa de la función. El dominio de la inversa de una función es igual a la imagen de la función original.
- Verifica si la función se repite. Cualquier función que se repita a lo largo del eje x tendrá la misma imagen para toda la función. Por ejemplo, f(x) = sen(x) tiene una imagen entre -1 y 1.
Referencias
- ↑ http://www.khanacademy.org/math/trigonometry/functions_and_graphs/domain_range/v/domain-and-range-of-a-relation
- ↑ http://www.uiowa.edu/~examserv/mathmatters/tutorial_quiz/geometry/findingvertexofparabola.html
- ↑ http://www.khanacademy.org/math/trigonometry/functions_and_graphs/domain_range/v/domain-and-range-of-a-relation
- ↑ http://www.khanacademy.org/math/trigonometry/functions_and_graphs/domain_range/v/domain-and-range-of-a-relation
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.mathsisfun.com/sets/domain-range-codomain.html
Acerca de este wikiHow
David Jia
Tutor académico
Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math. Este artículo ha sido visto 237 227 veces.
Categorías: Matemáticas
