Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 14 345 veces.
A menudo usarás una función para describir curvas y líneas en una gráfica de coordenadas, debido a que la función muestra la relación entre las coordenadas "x" y "y". Al igual que puedes sumar y restar números, también puedes sumar o restar funciones. Necesitas sumar y restar funciones al trabajar con diferentes tasas, escalas y medidas. Realizar simples operaciones en funciones no es más complicado que realizar esas operaciones en números.
Pasos
Método 1
Método 1 de 3:Sumar o restar funciones sin una variable
-
1Escribe las funciones que vas a sumar o restar. Las funciones por lo general se expresan como f(x) = relación, donde x es la variable y la relación se expresa como la fórmula para la variable x.[1] Debido a que vas a sumar o restar más de una función, estas van a identificarse de forma diferente, por lo general y .
- Por ejemplo, es muy probable que te pidan sumar la función y la función .
- Si te piden sumar las funciones, te piden que encuentres .
- Si te piden restar las funciones, te piden que encuentres .
-
2Acomoda las funciones según el grado de términos. Esto significa que debes ordenar la fórmula por exponentes, empezando por el exponente más grande ( etc.). Si no hay ningún exponente, anota el término de primer grado primero (x), seguido por las constantes (números sin variables).
- Por ejemplo, la función se acomoda de la siguiente manera . La función f(x) ya está ordenada por el grado de términos.
-
3Crea un problema de suma o resta usando las dos fórmulas. Puedes sumar o restar de forma horizontal o vertical, ya que ordenaste las funciones por términos.
- Por ejemplo, la función la puedes acomodar ,
o puedes acomodarla de forma vertical, alineando los términos:
.
- Por ejemplo, la función la puedes acomodar ,
-
4Suma o resta los términos iguales. Es útil sumar o restar por orden del grado de términos, empezando con el exponente más alto (si es que existe). [2]
- Por ejemplo, para , primero debes sumar los términos de primer grado:
.
Segundo, debes sumar las constantes:
.
Lo cual resulta en .
- Por ejemplo, para , primero debes sumar los términos de primer grado:
-
5Sigue el mismo proceso para sumar o restar más de dos funciones. Sumar o restar funciones siempre es cuestión de sumar o restar los términos iguales en las fórmulas de relación.
Método 2
Método 2 de 3:Sumar y restar funciones con la misma variable
-
1Suma o resta las funciones, como se describe en el primer método. Esto te dará la relación de la fórmula para tu variable (x).
- Por ejemplo, puedes encontrar que .
-
2Anota la variable. Recuerda, este método solo funciona al sumar o restar funciones con la misma variable.
- Por ejemplo, te puede preguntar que encuentres . La suma de la función lucirá de la siguiente manera: .
-
3Completa el cálculo. Recuerda usar el orden de las operaciones.
- Por ejemplo:
.
- Por ejemplo:
Método 3
Método 3 de 3:Sumar o restar funciones con diferentes variables
-
1Introduce las variables apropiadas en la primera función y resuelve el problema. Ya que estás trabajando con dos variables diferentes, no puedes sumar las fórmulas e introducir solo una, tienes que completar una función a la vez.[3]
- Por ejemplo, si tienes la siguiente ecuación y y te piden encontrar , primero necesitas encontrar . Cuando introduces el 2, obtienes:
.
- Por ejemplo, si tienes la siguiente ecuación y y te piden encontrar , primero necesitas encontrar . Cuando introduces el 2, obtienes:
-
2Anota la variable apropiada en la segunda función y resuelve la ecuación. Asegúrate de introducir la variable correcta en la función correcta.
- Por ejemplo, si , entonces:
- Por ejemplo, si , entonces:
-
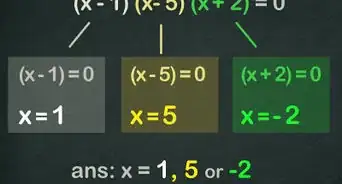
3Suma o resta los resultados. El resultado será la suma o resta de ambas funciones, dadas las variables previstas.
- Por ejemplo, si y , entonces:
.
- Por ejemplo, si y , entonces:
Cosas que necesitarás
- lápiz
- papel
- calculadora (opcional)




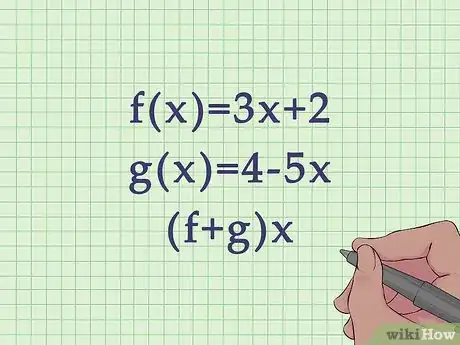






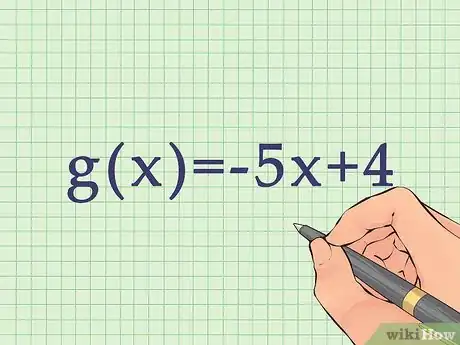


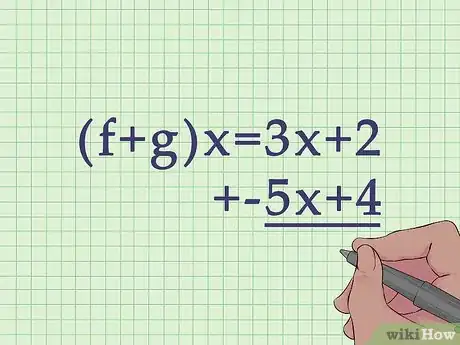


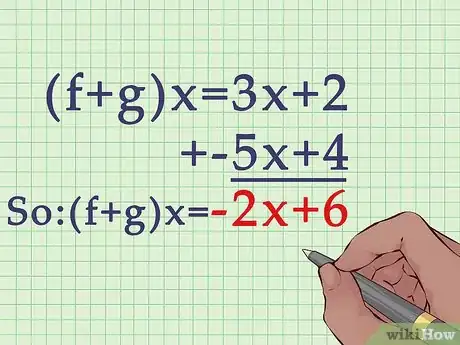



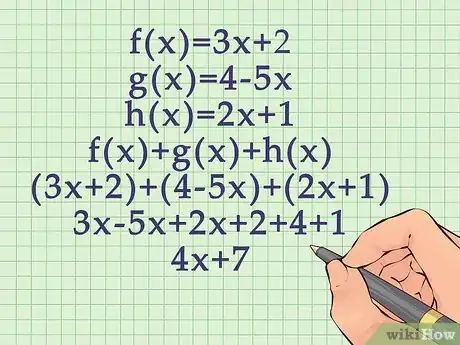
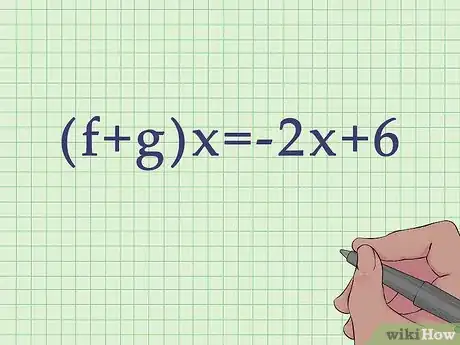
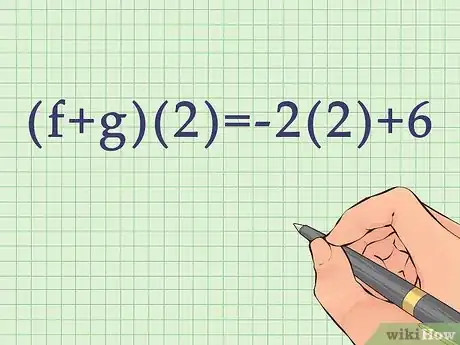


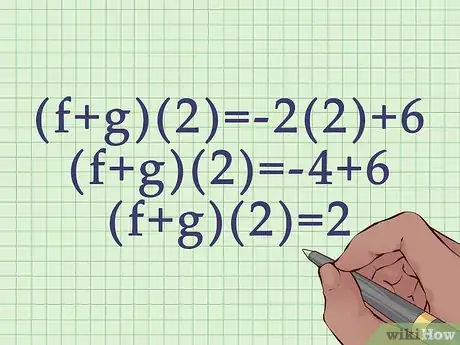


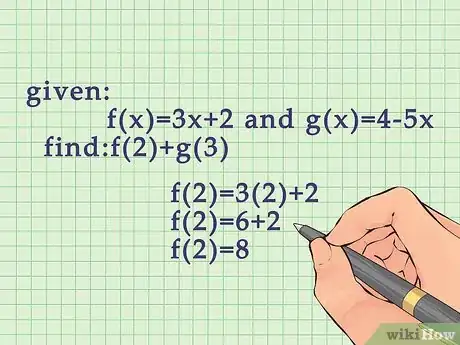





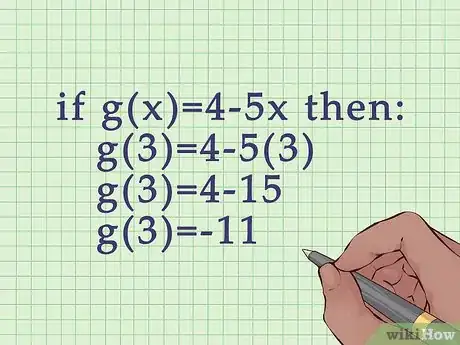



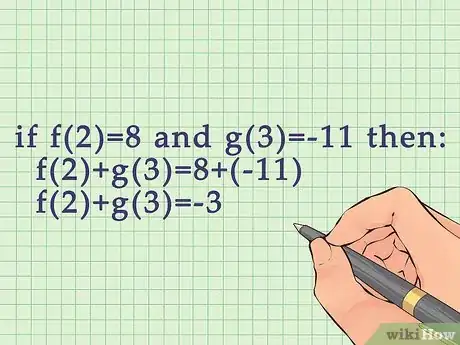





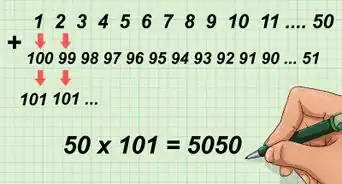

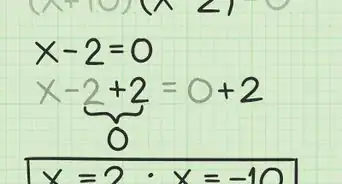
-Step-31-Version-2.webp)




wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 14 345 veces.