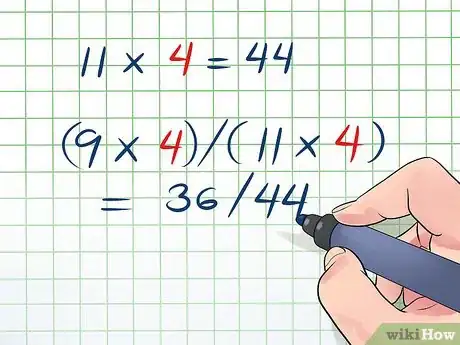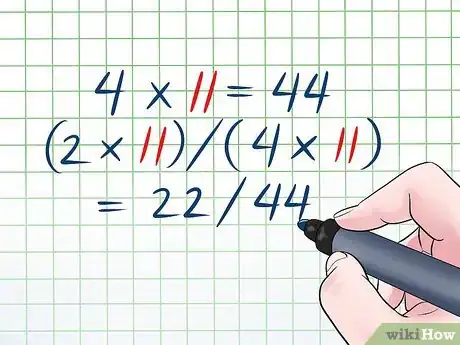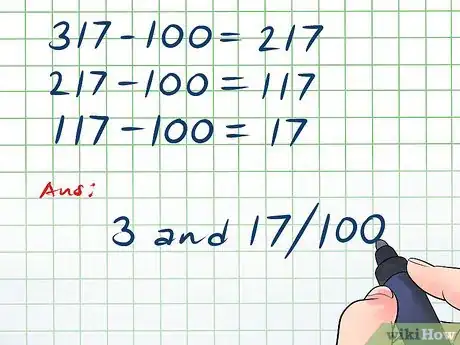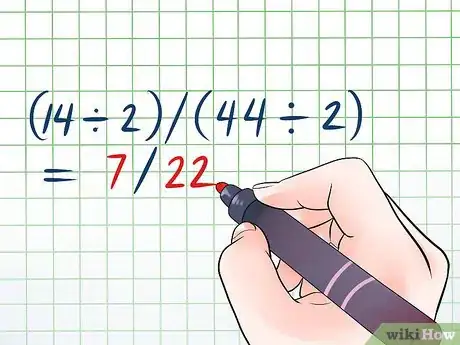Comment additionner et soustraire des fractions ayant des dénominateurs différents

Informations concernant l'auteur.e

Pour additionner et soustraire des fractions avec des dénominateurs différents, vous devez les convertir de manière à ce quelles aient le même dénominateur. Que vous souhaitiez effectuer une addition ou une soustraction, le procédé est le même jusqu'à la fin, où il faut soit ajouter, soit soustraire le numérateur d'une fraction à celui de l'autre. Dans les deux cas, la méthode est très simple.

Partie 1

Partie 1 sur 2:
Établir un dénominateur commun

1
Écrivez les deux fractions. Notez-les l'une à côté de l'autre, avec les numérateurs (les chiffres du haut) alignés ensemble sur la ligne du haut et les dénominateurs (les chiffres du bas) alignés ensemble en bas. Prenons un exemple avec les fractions ${\frac {9}{11}}$ et ${\frac {2}{4}}$ .
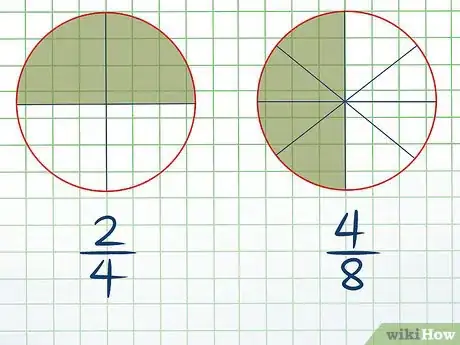
2
Comprenez le système d'équivalences. Si vous multipliez le numérateur et le dénominateur d'une fraction par le même nombre, vous obtenez une fraction équivalente à celle d'origine, c'est-à-dire qu'elle correspond à la même valeur. Par exemple, si vous prenez la fraction ${\frac {2}{4}}$ ${\frac {2}{4}}$ et que vous multipliez le numérateur et le dénominateur par 2, vous obtenez ${\frac {4}{8}}$ ${\frac {4}{8}}$ , qui équivaut à ${\frac {2}{4}}$ ${\frac {2}{4}}$ . Pour bien comprendre ce concept, vous pouvez utiliser une représentation graphique des fractions.
- Dessinez un cercle, divisez-le en quatre quartiers de taille égale et coloriez deux de ces quartiers. Cela représente la fraction ${\frac {2}{4}}$ .
- Dessinez un autre cercle, divisez-le en huit parts égales et coloriez-en quatre. Cela représente la fraction ${\frac {4}{8}}$ .
- Comparez les deux représentations. Les zones coloriées représentant ${\frac {2}{4}}$ et ${\frac {4}{8}}$ sont identiques.
3
Établissez un dénominateur commun. Pour ce faire, multipliez les dénominateurs des deux fractions entre eux. Avant de pouvoir additionner ou soustraire les fractions, il est indispensable de trouver des équivalences avec un dénominateur commun (c'est-à-dire que le chiffre du bas est le même pour les deux fractions). Le plus simple et rapide est de multiplier les deux dénominateurs entre eux. Une fois que vous aurez écrit le résultat, vous pourrez soit passer directement à la résolution de l'opération, soit passer à l'étape suivante pour trouver un dénominateur commun plus petit et facile à utiliser.
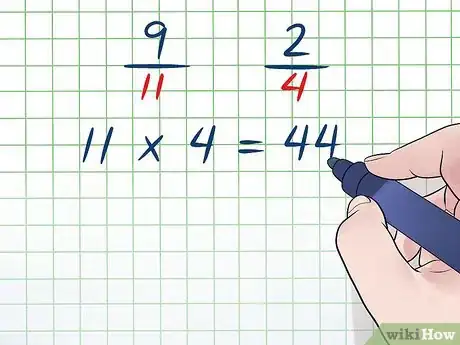
- Par exemple, nous avons commencé avec les fractions ${\frac {9}{11}}$ et ${\frac {2}{4}}$ , dont les dénominateurs sont 11 et 4.
- Multipliez ces deux dénominateurs : $11\times 4=44$ .
4
Réduisez le dénominateur commun. Cette étape est facultative. La méthode ci-dessus est rapide, mais il peut être utile de chercher le dénominateur commun le plus petit possible. Pour ce faire, notez les multiples de chacun des deux dénominateurs et repérez le nombre le plus petit qui figure dans les deux listes. Prenons comme exemple l'addition ${\frac {5}{6}}+{\frac {2}{9}}$ ${\frac {5}{6}}+{\frac {2}{9}}$ .
- Étant donné que les dénominateurs sont 6 et 9, vous devez utiliser les tables de multiplication de 6 et de 9 pour trouver les multiples appropriés.
- Les multiples de 6 sont : 6, 12, 18, 24, etc.
- Les multiples de 9 sont : 9, 18, 27, 36, etc.
- Étant donné que 18 figure dans les deux listes, il peut servir de dénominateur commun.
Publicité

Partie 2

Partie 2 sur 2:
Effectuer le reste de l'opération

1
Modifiez la première fraction. Faites-en une fraction équivalente en utilisant le dénominateur commun que vous avez trouvé. Dans notre premier exemple avec les fractions ${\frac {9}{11}}$ ${\frac {9}{11}}$ et ${\frac {2}{4}}$ ${\frac {2}{4}}$ , nous avons établi 44 comme dénominateur commun. Cependant, il ne suffit pas de remplacer le dénominateur. Il faut aussi multiplier le numérateur par le même nombre. Voici comment trouver une fraction équivalente à celle d'origine.
- Nous savons que $11\times 4=44$ (c'est comme cela que nous avons établi le dénominateur commun, mais si vous l'aviez oublié, vous pouvez aussi calculer $44\div 11$ ).
- Multipliez les deux parties de la fraction par le même nombre pour obtenir une fraction équivalente.
- ${\frac {9\times 4}{11\times 4}}={\frac {36}{44}}$
2
Adaptez la deuxième fraction. Faites la même chose que pour la première. Dans notre exemple, la deuxième fraction est ${\frac {2}{4}}$ ${\frac {2}{4}}$ . Transformez-la de la façon suivante de manière à ce qu'elle comporte aussi le dénominateur commun.
- $4\times 11=44$
- ${\frac {2\times 11}{4\times 11}}={\frac {22}{44}}$
3
Terminez l'opération. Ajoutez ou soustrayez les numérateurs des fractions pour trouver la réponse. Une fois qu'elles ont un dénominateur commun, il vous suffit d'additionner ou de soustraire leurs numérateurs modifiés pour trouver le résultat.
- Pour une addition : ${\frac {36}{44}}+{\frac {22}{44}}={\frac {36+22}{44}}={\frac {58}{44}}$
- Pour une soustraction : ${\frac {36}{44}}-{\frac {22}{44}}={\frac {36-22}{44}}={\frac {14}{44}}$
4
Convertissez les fractions impropres. Faites-en des nombres mixtes. Une fraction est dite « impropre » lorsque son numérateur est supérieur à son dénominateur, c'est-à-dire qu'elle correspond à une valeur supérieure à 1. Vous pouvez transformer ce type de fraction en « nombre mixte » plus facile à lire en divisant le numérateur par le dénominateur et en conservant le reste de la division dans une nouvelle fraction avec le dénominateur d'origine. Par exemple, pour la fraction ${\frac {58}{44}}$ ${\frac {58}{44}}$ , il faut faire la division suivante : $58\div 44=1$ $58\div 44=1$ , avec pour reste 14. Cela signifie que le nombre mixte correspondant à la fraction est 1 et 14/44.
- Si vous ne savez pas comment effectuer une division longue, vous pouvez simplement soustraire le nombre du bas à celui du haut autant de fois que possible et noter le nombre de fois que vous l'avez soustrait. Par exemple, la fraction ${\frac {317}{100}}$ peut se convertir de la façon suivante.
- $317-100=217$ (vous avez soustrait 100 à 317 une fois). $217-100=117$ (vous avez soustrait 100 deux fois). $117-100=17$ (vous avez soustrait 100 trois fois). Vous ne pouvez plus soustraire 100 au résultat, il y a donc un reste de 17 et le nombre mixte qui correspond à la fraction est 3 et 17/100.
5
Simplifiez le résultat. Le fait de simplifier une fraction consiste à l'écrire sous la forme de l'équivalence la plus petite possible de façon à ce qu'elle soit plus facile à utiliser. Divisez le numérateur et le dénominateur par le même nombre. Continuez de le faire jusqu'à ce que ne soit plus du tout possible. Par exemple, vous pouvez simplifier ${\frac {14}{44}}$ ${\frac {14}{44}}$ de la façon suivante.
- 14 et 44 peuvent tous deux être divisés par 2.
- ${\frac {14\div 2}{44\div 2}}={\frac {7}{22}}$
- Étant donné qu'il n'y a aucun nombre permettant de diviser à la fois 7 et 22, la fraction simplifiée finale est ${\frac {7}{22}}$ .
Publicité

Exemples d'opérations

Essayez de résoudre les opérations suivantes. Lorsque vous pensez avoir trouvé la réponse, sélectionnez ou surlignez le texte invisible après le signe = pour vérifier le résultat et voir si vous avez raison. Les opérations dans chaque section deviennent de plus en plus difficiles à mesure que vous progressez. Les dernières sont difficiles et vous ne trouverez pas forcément la bonne réponse du premier coup à chaque fois.

Exemples d'additions

${\frac {1}{2}}+{\frac {3}{8}}$ = 7/8
${\frac {2}{5}}+{\frac {1}{3}}$ = 11/15
${\frac {3}{4}}+{\frac {4}{8}}$ = 1 et 1/4
${\frac {10}{3}}+{\frac {3}{9}}$ = 3 et 2/3
${\frac {5}{6}}+{\frac {8}{5}}$ = 2 et 13/30
${\frac {2}{17}}+{\frac {4}{5}}$ = 78/85

Exemples de soustractions

${\frac {2}{3}}-{\frac {5}{9}}$ = 1/9
${\frac {15}{20}}-{\frac {3}{5}}$ = 3/20
${\frac {7}{8}}-{\frac {7}{9}}$ = 7/72
${\frac {3}{5}}-{\frac {4}{7}}$ = 1/35
${\frac {7}{12}}-{\frac {3}{8}}$ = 5/24
${\frac {16}{5}}-{\frac {1}{4}}$ = 2 et 19/20

Conseils

Le dénominateur commun le plus petit peut être abrégé sous la forme PPCM (« Plus Petit Commun Multiple »). Lorsque le PPCM est appliqué à des fractions, il s'agit du nombre le plus petit qui est un multiple des dénominateurs différents.