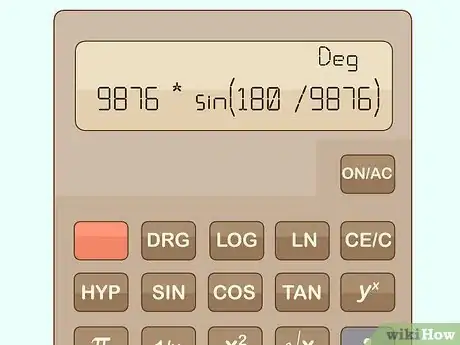Comment calculer Pi

La constante pi (π) est l´un des chiffres les plus importants et les plus fascinants du monde des mathématiques. Le fameux 3,14 est une constante utilisée pour calculer la circonférence d'un cercle à partir de son rayon. C'est un nombre irrationnel, puisqu'il ne peut pas s'écrire sous la forme d'un rapport de deux entiers, son écriture est faite d'une infinité de décimales, sans aucune périodicité. On ne connaitra jamais toutes ses décimales.

Méthode 1
Méthode 1 sur 5:
Calculer la constante pi à partir des mesures d'un cercle

  1. Image intitulée 1964913 1
    1
    Vérifiez que votre figure soit un cercle. La méthode de calcul que nous allons voir ne marche que pour les cercles, non les ellipses ou tout autre ovoïde. Le cercle est une figure géométrique délimitée par une courbe dont tous les points sont à égale distance d'un centre. Pour dessiner un cercle, prenez un compas ou prenez comme modèle un couvercle rond et lisse. Utilisez la mine de crayon la plus fine que vous pouvez. Si vous prenez un crayon mal taillé, vous risquez alors d'avoir un grand écart au moment de calculer π. Plus votre trait sera fin, mieux ce sera.
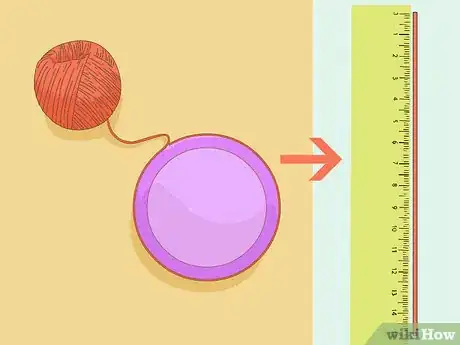
  2. Image intitulée 1964913 2
    2
    Mesurez précisément la circonférence de votre cercle. La circonférence du cercle est en fait son périmètre, c'est-à-dire la longueur de la ligne qui délimite le cercle. La mesure d'une circonférence est difficile, car elle est courbe, et c'est là qu'intervient la constante π.
    • À l'aide d'une ficelle fine, essayez de suivre le plus exactement possible le contour du cercle. Faites sur la ficelle un repère qui marque un tour complet. Retirez la ficelle et mesurez-la avec une règle.
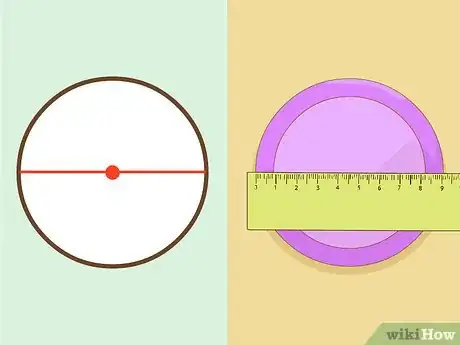
  3. Image intitulée 1964913 3
    3
    Mesurez le diamètre du cercle. Le diamètre (D) est la longueur qui va d'un point du cercle à un point opposé en passant par le centre.
  4. Image intitulée Calculate Pi Step 4
    4
    Utilisez la formule de la circonférence. La circonférence (C) d'un cercle est donnée par une formule bien connue des écoliers : . En conséquence, π est égal à la circonférence divisée par le diamètre. Remplacez les lettres par les valeurs que vous avez trouvées et prenez votre calculatrice : vous devriez trouver une valeur proche de 3,14[1] .
  5. Image intitulée Calculate Pi Step 5
    5
    Confirmez votre résultat. Pour affiner votre résultat, répétez l'opération avec des cercles de tailles différentes, puis faites une moyenne des résultats trouvés. Certes, toutes ces mesures sont approximatives, mais en multipliant les mesures, vous devriez obtenir une valeur de π assez précise.
    Publicité

Méthode 2
Méthode 2 sur 5:
Calculer la constante pi en utilisant une série infinie

  1. Image intitulée Calculate Pi Step 6
    1
    Utilisez la formule de Leibniz-Grégory. Des mathématiciens ont travaillé sur π et ont établi des séries de calculs qui, répétés à l'infini, permettent d'approcher de la vraie valeur de π. Ces formules se programment facilement et les ordinateurs d'aujourd'hui sont capables de calculer un très grand nombre de ces décimales. La suite la plus simple est celle de Leibniz-Grégory. Cette formule est moyennement efficace à calculer les décimales de π (cinq décimales seulement pour 500 000 fractions)[2] . La formule est la suivante :
    • Faites 4 divisé par 1, puis soustrayez 4 divisé par 3, puis ajoutez 4 divisé par 5, puis soustrayez 4 divisé par 7, etc. Alternez les additions et les soustractions de fractions ayant toujours 4 en numérateur et en dénominateur, un nombre impair croissant. Plus vous ferez de calculs, plus précise sera votre valeur.
  2. Image intitulée Calculate Pi Step 7
    2
    Essayez la formule de Nilakantha. C'est une autre façon de calculer les décimales de π. Elle ressemble à la précédente, mais en diffère par les dénominateurs. Peut-être est-elle un plus compliquée en ce qui concerne les calculs, mais la convergence vers π est plus rapide (11 décimales pour 10 000 fractions).
    • Ici aussi, on alterne aussi les additions et les soustractions de fractions ayant toujours 4 en numérateur. La différence réside dans le dénominateur qui est le produit de trois entiers successifs. À la fraction suivante, le premier élément du produit est le dernier élément du produit précédent. Testez cette formule et vous obtiendrez rapidement une valeur assez précise de π.
    Publicité

Méthode 3
Méthode 3 sur 5:
Calculer la constante pi par la méthode de Buffon

  1. Image intitulée Calculate Pi Step 8
    1
    Jetez des objets allongés sur un parquet. Aussi étrange que cela paraisse, il est possible d'avoir une approximation de π en jetant sur un sol marqué de lignes parallèles des objets identiques et allongés comme des saucisses. C'est qu'a fait Buffon au XVIIIe siècle : cette expérience porte le nom d'« aiguille de Buffon ». Il aurait remarqué qu'en jetant des aiguilles (un très grand nombre) sur un parquet, on pouvait obtenir une approximation de π. Pour cela, il faut des aiguilles qui ont comme longueur la largeur des lattes du parquet. La probabilité que l'aiguille coupe le bord d'une latte serait de . Cette méthode n'est pas très précise, car il a été prouvé que pour avoir une valeur de π au millième, il fallait lancer 900 000 aiguilles !
    • Dans le passé, et encore aujourd'hui, des scientifiques de toutes les spécialités ont calculé la valeur de π la plus précise qui soit. Actuellement, on connait plus de 13 300 milliards de décimales[3] .

Méthode 4
Méthode 4 sur 5:
Calculer la constante pi en utilisant la limite d'une fonction

  1. Image intitulée Calculate Pi Step 9
    1
    Choisissez un grand nombre. Plus ce nombre sera élevé, plus précise sera votre valeur de π. Cette valeur sera appelée x.
  2. Image intitulée Calculate Pi Step 10
    2
    Faites l'application numérique. Remplacez x par la valeur que vous avez choisie dans la fonction suivante : . Votre calculatrice devra être réglée sur les degrés, sinon cela ne marche pas. En fait, la limite de cette fonction est π, le demi-cercle (180°) valant π. Si vous faites un tel calcul plusieurs fois de suite, avec chaque fois une valeur plus élevée, vous aurez une valeur de π de plus en plus précise.
    Publicité

Méthode 5
Méthode 5 sur 5:
Calculer la constante pi en utilisant la fonction arcsinus

  1. Image intitulée Calculate Pi Step 11
    1
    Choisissez un chiffre entre -1 et 1. Cette limite s'explique par le fait qu'on va utiliser la fonction arcsinus qui n'admet pas de valeurs extérieures à l'intervalle [-1, 1].
  2. Image intitulée Calculate Pi Step 12
    2
    Entrez le nombre choisi dans la formule qui suit. Vous devriez trouver une valeur de π assez fidèle.
      • La fonction arcsinus est la fonction réciproque de la fonction sinus. Pour cette fonction, les valeurs à entrer sont toujours en radians.
      • La touche est celle qui calcule la racine carrée.
      • La touche est celle qui calcule la valeur absolue.
      • La touche est celle qui permet de calculer le carré d'une valeur.
    Publicité

Conseils

  • Calculer π est certes amusant, même si c'est un défi, mais l'important est de savoir de combien de décimales on a besoin. Ainsi, les astrophysiciens affirment n'avoir besoin pour leurs calculs (et ils aiment la précision !) que de 39 décimales.
Publicité

wikiHows en relation

calculer l'inverse d'une matrice 3x3
Comment
calculer l'inverse d'une matrice 3x3
calculer un pourcentage d'augmentation
Comment
calculer un pourcentage d'augmentation
calculer le diamètre d'un cercle
Comment
calculer le diamètre d'un cercle
calculer la hauteur d'un triangle
Comment
calculer la hauteur d'un triangle
calculer la valeur de résistances en série ou en dérivation
Comment
calculer la valeur de résistances en série ou en dérivation
calculer le déterminant d'une matrice 3 x 3
Comment
calculer le déterminant d'une matrice 3 x 3
calculer un écart type
Comment
calculer un écart type
calculer le rayon d’un cercle
Comment
calculer le rayon d’un cercle
calculer la diagonale d’un rectangle
Comment
calculer la diagonale d’un rectangle
calculer la longueur de l'hypoténuse
Comment
calculer la longueur de l'hypoténuse
calculer un intervalle de confiance
Comment
calculer un intervalle de confiance
calculer une racine carrée à la main
Comment
calculer une racine carrée à la main
calculer les probabilités de gagner à la loterie
Comment
calculer les probabilités de gagner à la loterie
calculer l’angle entre deux vecteurs
Comment
calculer l’angle entre deux vecteurs
Publicité

Références

  1. ↑ http://www.mathsisfun.com/numbers/pi.html
  2. ↑ https://fr.wikipedia.org/wiki/Pi
  3. ↑ http://therese.eveilleau.pagesperso-orange.fr//pages/truc_mat/textes/buffon.htm

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 38 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 112 734 fois.
Catégories: Calculs
Résumé de l'articleX

Pour avoir la valeur de pi, déterminez la circonférence d'un cercle en l'entourant au plus juste avec une ficelle. À l'aide d'une règle, mesurez ensuite ce morceau de ficelle. Avec la même règle, mesurez le diamètre du cercle, c'est la distance qui va d'un point d'un cercle au point opposé en passant par le centre. Vous avez à présent la circonférence et le diamètre de votre cercle, il ne vous reste plus qu'à diviser la circonférence par le diamètre, et le résultat obtenu ne sera rien d'autre que la valeur de pi.

Publicité