Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 8 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 48 898 fois.
Un cercle est une figure du plan formée d'un ensemble de points qui sont tous situés à la même distance du centre dudit cercle [1] . La circonférence (C) d'un cercle est son périmètre, c'est-à-dire la longueur de la ligne qui délimite le contour du cercle [2] . L'aire (A) d'un cercle est la surface comprise à l'intérieur du cercle [3] . Que soit pour l'aire ou pour la circonférence, le calcul est facile : vous n'avez besoin que du rayon ou du diamètre et de pi.
Étapes
Partie 1
Partie 1 sur 3:Calculer la circonférence d'un cercle
-
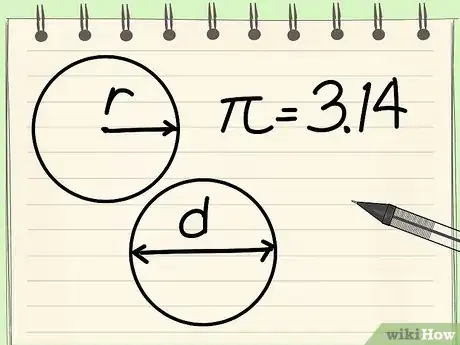
1Apprenez par cœur la formule de la circonférence d'un cercle. Il y a deux formules de calcul pour obtenir la circonférence (C) d'un cercle : C = 2πr ou C = πd, formules dans lesquelles π est la constante bien connue, valant à peu près 3,14 [4] , r représente le rayon et d, le diamètre [5] .
- Ces deux formules sont évidentes dans la mesure où le diamètre est égal à deux fois le rayon (d = 2r) et partant, le rayon est égal à la moitié du diamètre (r = d/2).
- Une circonférence s'exprime obligatoirement avec des unités de longueur : des centimètres (cm), des mètres (m), des kilomètres (km), des milles nautiques (ml)…
-
2Comprenez bien les différents termes de la formule. Vous allez avoir besoin de 2 ou 3 éléments pour calculer la circonférence d'un cercle : le rayon ou le diamètre et π. Rayon et diamètre sont liés, puisque le rayon est la moitié du diamètre et donc, le diamètre est le double du rayon.
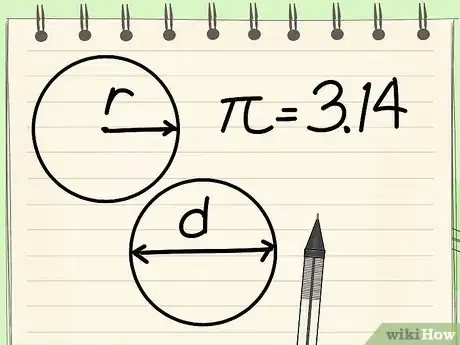
- Le rayon (r) d'un cercle est la distance du centre du cercle à n'importe quel point de la circonférence.
- Le diamètre (d) d'un cercle est la distance d'un point du cercle à son point opposé, en passant obligatoirement par le centre [6] .
- La lettre grecque pi (π) est le rapport entre la circonférence et le diamètre d'un cercle. Il équivaut à 3,14159265…, c'est un nombre irrationnel sans fin et qui n'a aucune période [7] . Cette constante est souvent arrondie à 3,14 pour faciliter les calculs.
-
3Mesurez le rayon ou le diamètre du cercle. Utilisez pour cela une règle, vous placerez le zéro sur le cercle et vous ferez passer la règle par le centre du cercle. La distance que vous mesurerez jusqu'au centre du cercle sera le rayon, tandis que celle qui ira du point choisi jusqu'au point opposé en passant par le centre sera le diamètre
- Dans les exercices qu'on vous donnera à l'école pour vous entrainer, il y aura souvent soit le rayon soit le diamètre.
-
4Faites l'application numérique, puis calculez. Une fois le rayon (ou le diamètre) du cercle déterminé, vous pouvez alors remplacer les valeurs littérales par leurs vraies valeurs. Si vous avez le rayon, prenez la formule : C = 2πr, mais si c'est le diamètre, prenez l'autre formule : C = πd.
- Exercice : quelle est la circonférence d'un cercle de 3 cm de rayon ?
- Notez la formule : C = 2πr
- Faites l'application numérique : C = 2π3
- Faites le produit : C = 2 x 3 x π = 6π = 6 x 3,14 =18,84 cm
- Exercice : quelle est la circonférence d'un cercle de 9 m de diamètre ?
- Notez la formule : C = πd
- Faites l'application numérique : C = 9π
- Faites le produit : C = 9 x π = 9 x 3,14 = 28,26 m
- Exercice : quelle est la circonférence d'un cercle de 3 cm de rayon ?
-
5Exercez-vous avec des problèmes. Maintenant que vous connaissez les formules, vous pouvez passer à la pratique. Plus vous résoudrez de problèmes ou d'exercices, mieux vous y arriverez, meilleures seront vos notes.
- Exercice : trouvez la circonférence d'un cercle de 5 cm de diamètre.
- C = πd = 5π = 5 x 3,14 = 15,7 cm
- Exercice : trouvez la circonférence d'un cercle de 10 cm de rayon.
- C = 2πr = 2π10 = 2 x 10 x π = 20 x 3,14 = 62,8 cm
Publicité - Exercice : trouvez la circonférence d'un cercle de 5 cm de diamètre.
Partie 2
Partie 2 sur 3:Calculer l'aire d'un cercle
-
1Apprenez par cœur la formule de l'aire d'un cercle. On peut calculer l'aire (A) d'un cercle en utilisant soit le diamètre soit le rayon. On a donc deux formules à notre disposition : A = πr2 ou A = π(d/2)2 [8] , formules dans lesquelles π est la constante bien connue, valant à peu près 3,14 [9] , r représente le rayon et d, le diamètre.
- Ces deux formules sont évidentes dans la mesure où le diamètre est égal à deux fois le rayon (d = 2r) et partant, le rayon est égal à la moitié du diamètre (r = d/2).
- Une aire s'exprime obligatoirement avec des unités de surface : des centimètres carrés (cm2), des mètres carrés (m2), des kilomètres carrés (km2), des milles carrés (ml2)…
-
2Comprenez bien les différents termes de la formule. Vous allez avoir besoin de 2 ou 3 éléments pour calculer la circonférence d'un cercle : le rayon ou le diamètre et π. Rayon et diamètre sont liés, puisque le rayon est la moitié du diamètre et donc, le diamètre est le double du rayon.
- Le rayon (r) d'un cercle est la distance du centre du cercle à n'importe quel point de la circonférence.
- Le diamètre (d) d'un cercle est la distance d'un point du cercle à son point opposé, en passant obligatoirement par le centre [10] .
- La lettre grecque pi (π) est le rapport entre la circonférence et le diamètre d'un cercle. Il équivaut à 3,14159265…, c'est un nombre irrationnel sans fin et qui n'a aucune période [11] . Cette constante est souvent arrondie à 3,14 pour faciliter les calculs.
-
3Mesurez le rayon ou le diamètre du cercle. Utilisez pour cela une règle, vous placerez le zéro sur le cercle et vous ferez passer la règle par le centre du cercle. La distance que vous mesurerez jusqu'au centre sera le rayon, tandis que celle qui ira du point choisi jusqu'au point opposé en passant par le centre sera le diamètre.
- Dans les exercices qu'on vous donnera à l'école pour vous entrainer, il y aura souvent soit le rayon soit le diamètre.
-
4Faites l'application numérique, puis les calculs. Une fois le rayon (ou le diamètre) du cercle déterminé, vous pouvez alors remplacer les valeurs littérales par leurs vraies valeurs. Si vous avez le rayon, prenez la formule : A = πr2, si c'est le diamètre, prenez l'autre formule : A = π(d/2)2.
- Exercice : quelle est l'aire d'un cercle de 3 m de rayon ?
- Prenez la formule suivante : A = πr2
- Faites l'application numérique : A = π32
- Élevez le rayon au carré : r2 = 32 = 9
- Multipliez par pi : A = 9π = 9 x 3,14 = 28,26 m2
- Exercice : quelle est l'aire d'un cercle de 4 m de diamètre ?
- Prenez la formule suivante : A = π(d/2)2
- Faites l'application numérique : A = π(4/2)2
- Divisez le diamètre par 2 : d/2 = 4/2 = 2
- Élevez au carré le résultat obtenu : 22 = 4
- Multipliez par pi : A = 4π = 4 x 3,14 = 12,56 m2
- Exercice : quelle est l'aire d'un cercle de 3 m de rayon ?
-
5Exercez-vous avec des problèmes. Maintenant que vous connaissez les formules, vous pouvez passer à la pratique. Plus vous résoudrez de problèmes ou d'exercices, mieux vous y arriverez, meilleures seront vos notes.
- Exercice : trouvez l'aire d'un cercle de 7 cm de diamètre
- A = π(d/2)2 = π(7/2)2 = π(3,5)2 = 12,25 x π = 12,25 x 3,14 = 38,47 cm2
- Exercice : trouvez l'aire d'un cercle de 3 cm de rayon
- A = πr2 = π32 = 9 x π = 9 x 3,14 = 28,26 cm2
Publicité - Exercice : trouvez l'aire d'un cercle de 7 cm de diamètre
Partie 3
Partie 3 sur 3:Calculer l'aire et la circonférence d'un cercle avec des inconnues
-
1Déterminez le rayon ou le diamètre du cercle. Dans certains exercices, on vous donnera comme rayon ou comme diamètre une inconnue : r = (x + 7) ou d = (x + 3). Dans ce cas, les formules de l'aire et de la circonférence restent les mêmes, seulement votre résultat final contiendra l'inconnue. Inscrivez le rayon ou le diamètre tel qu'il vous ait donné.
- Exercice : calculez la circonférence d'un cercle de (x +1) de rayon.
-
2Récrivez la formule adéquate. Vous remplacerez les valeurs littérales par les valeurs qu'on vous a données. Cette démarche est valable aussi bien pour le calcul de la circonférence que celui de l'aire. Après avoir rappelé la formule de l'aire ou de la circonférence, faites l'application numérique avec l'inconnue.
- Exercice : calculez la circonférence d'un cercle de rayon (x + 1).
- La formule de calcul est : C = 2πr
- Faites l'application numérique : C = 2π(x+1)
-
3Faites les calculs. Opérez comme si l'inconnue était un nombre. Il n'est pas question de trouver un chiffre ou un nombre ici, puisqu'on a au départ une inconnue qu'on traitera cependant comme un nombre. Vous serez peut-être obligé d'utiliser la distributivité de la multiplication pour trouver le résultat.
- Exercice : calculez la circonférence d'un cercle de rayon (x + 1).
- C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = (2 x 3,14)x + (2 x 3,14) = 6,28x + 6,28
- Si par la suite on vous donne une valeur pour x, il suffira de remplacer dans votre résultat, x par sa valeur.
-
4Exercez-vous avec des problèmes. Maintenant que vous connaissez les formules, vous pouvez passer à la pratique.Plus vous résoudrez de problèmes ou d'exercices, mieux vous y arriverez, meilleures seront vos notes.
- Exercice : trouvez l'aire d'un cercle de 2x de rayon.
- A = πr2 = π(2x)2 = π4x2 = 4 x 3,14x2 =12,56x2
- Exercice : trouvez l'aire d'un cercle de (x + 2) de diamètre.
- A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π
Publicité - Exercice : trouvez l'aire d'un cercle de 2x de rayon.
Références
- ↑ http://www.mathopenref.com/circle.html
- ↑ http://www.mathopenref.com/circumference.html
- ↑ http://www.mathopenref.com/circlearea.html
- ↑ http://www.mathopenref.com/pi.html
- ↑ http://www.mathopenref.com/circumference.html
- ↑ http://www.mathopenref.com/diameter.html
- ↑ https://www.mathsisfun.com/definitions/pi.html
- ↑ http://www.mathgoodies.com/lessons/vol2/circle_area.html
- ↑ http://www.mathopenref.com/pi.html

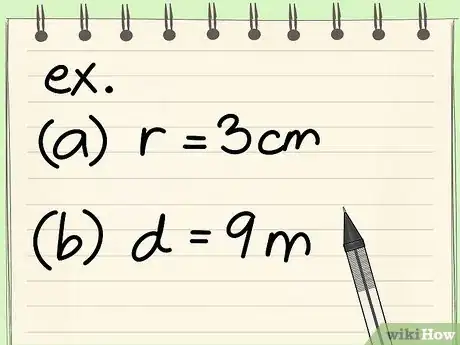
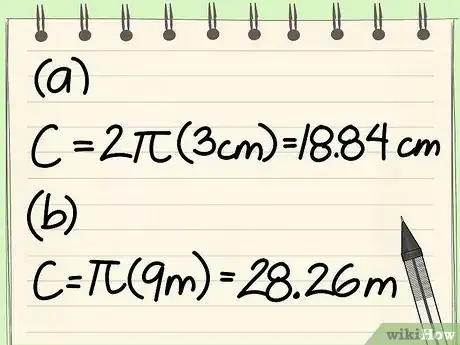
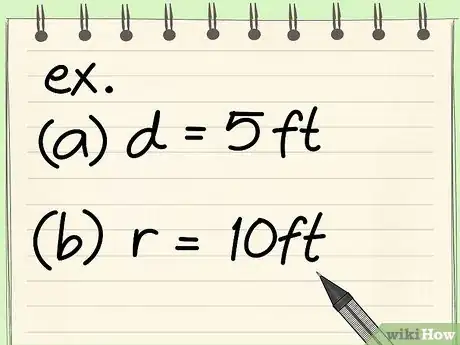

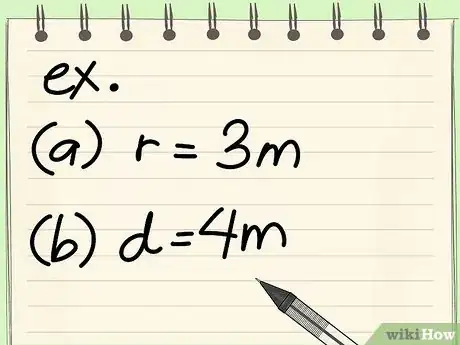
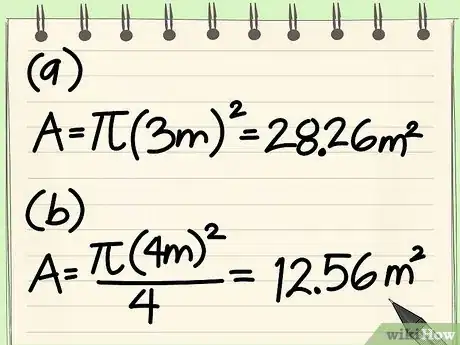
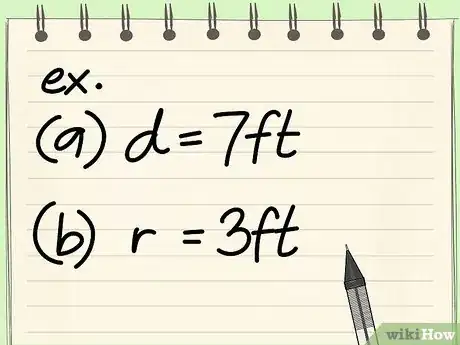
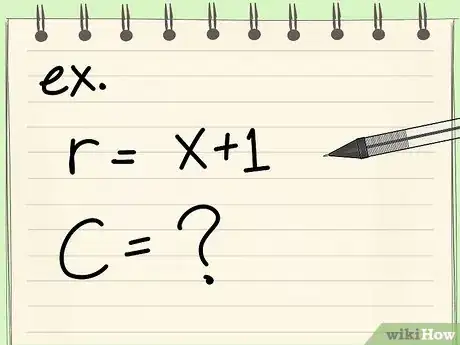
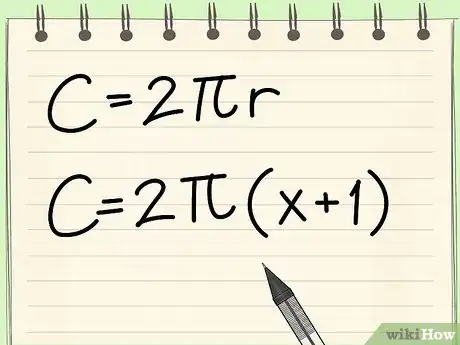
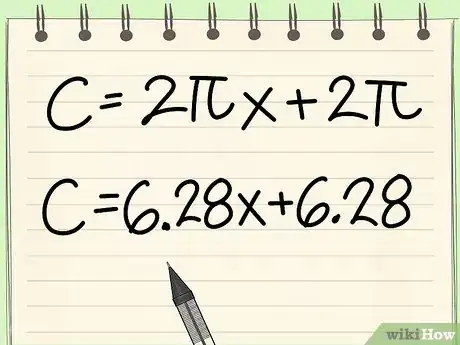
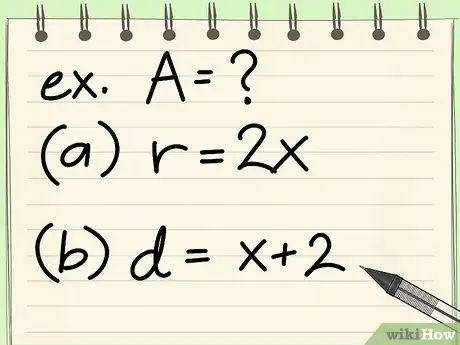



















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 48 898 fois.