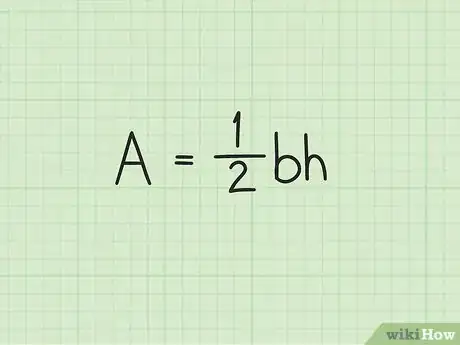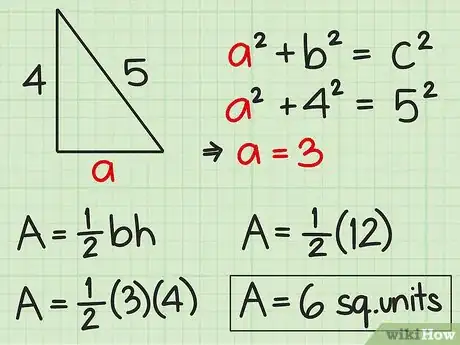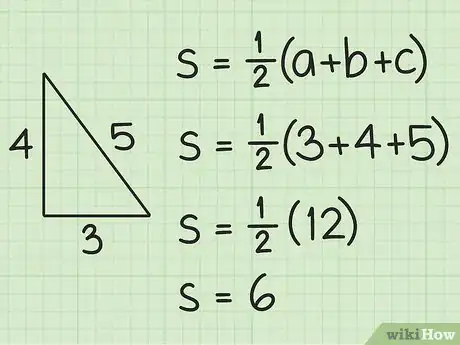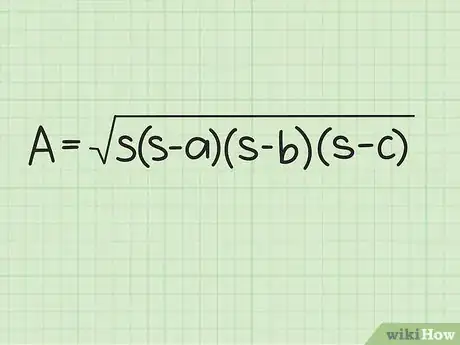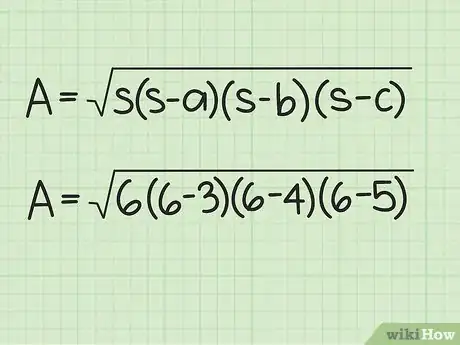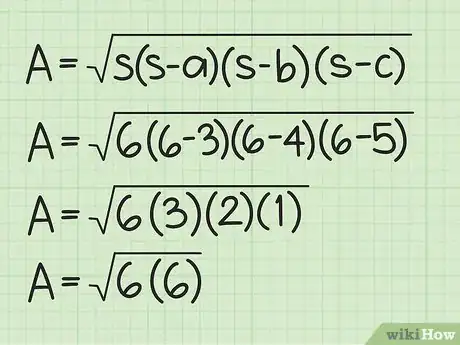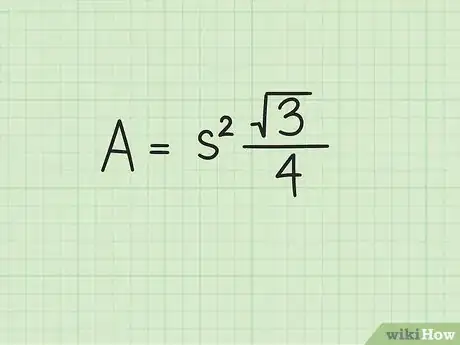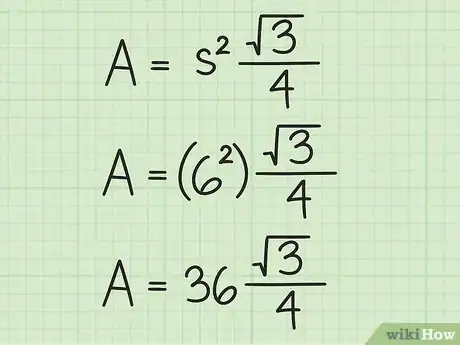Comment calculer la surface d'un triangle

Coécrit par David Jia

Pour trouver l'aire d'un triangle quelconque, la méthode la plus courante consiste à prendre la moitié du produit de la base par la hauteur. Cette formule marche pour tous les triangles. Cependant, il existe de nombreuses autres formules, qui toutes dépendent en fait des informations qui vous ont été données. Ainsi, il est possible de calculer l'aire d'un triangle sans connaitre la hauteur, il suffit d'avoir les côtés du triangle et les angles.

Méthode 1

Méthode 1 sur 4:
Calculer l'aire d'un triangle en utilisant la base et la hauteur

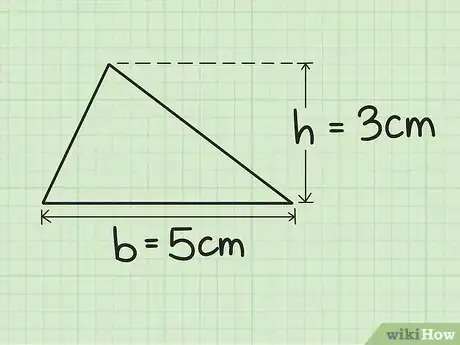
1
Trouvez la base et la hauteur d'un triangle. Par définition, la base d'un triangle est le côté sur lequel il repose. La hauteur est la ligne qui part du sommet opposé à la base et qui se termine sur la base, mais à ange droit. Ces informations peuvent vous être données dans l'énoncé d'un exercice. Vous pouvez aussi les mesurer si vous avez une figure qui accompagne l'exercice.
- Prenons l'exemple d'un triangle qui aurait une base de cinq centimètres (5 cm) et une hauteur de trois centimètres (3 cm).
2
Inscrivez la formule de calcul de l'aire d'un triangle. Elle est la suivante : ${\text{Aire}}={\frac {1}{2}}(bh)$ , formule dans laquelle $b$ est la longueur de la base du triangle et $h$ , la hauteur du triangle ^{[1]
X
Source de recherche}.
3
Faites l'application numérique. Remplacez les lettres de la formule par leurs valeurs respectives. Multipliez en premier ces deux valeurs, puis ce résultat par ${\frac {1}{2}}$ ${\frac {1}{2}}$ . Vous obtenez l'aire de votre triangle en unités carrées.
- Reprenons notre exemple : on a un triangle dont la base est de 5 cm et dont la hauteur est de 3 cm, la formule s'établit ainsi :
  ${\text{Aire}}={\frac {1}{2}}(bh)$
  
  ${\text{Aire}}={\frac {1}{2}}(5)(3)$
  
  ${\text{Aire}}={\frac {1}{2}}(15)$
  
  ${\text{Aire}}=7,5$
  En conséquence, l'aire d'un triangle ayant une base of 5 cm et une hauteur de 3 cm est de 7,5 cm².
4
Trouvez l'aire d'un triangle rectangle. Comme deux côtés d'un triangle rectangle sont perpendiculaires, un de ces côtés sera la hauteur du triangle, et par déduction, l'autre sera la base. En fait, avec un tel triangle, on a d'office les longueurs de la base et de la hauteur, sans que ces noms soient cités. En conséquence, vous pouvez utiliser la formule ${\text{Aire}}={\frac {1}{2}}(bh)$ ${\text{Aire}}={\frac {1}{2}}(bh)$ pour trouver l'aire.
- Vous pouvez également utiliser cette formule si vous connaissez la longueur d'un des côtés et celle de l'hypoténuse. L'hypoténuse est le plus long des trois côtés et est opposée à l'angle droit. Dès lors que vous connaissez deux des trois côtés d'un triangle rectangle, il est toujours possible, grâce au théorème de Pythagore ( $a^{2}+b^{2}=c^{2}$ ), de trouver le côté manquant.
- Traditionnellement, l'hypoténuse d'un triangle est le côté c, et la hauteur et la base sont les côtés a et b. Si l'énoncé de l'exercice donne une hypoténuse de 5 cm et une base de 4 cm, utilisez le théorème de Pythagore pour trouver le troisième côté, soit la hauteur :
  $a^{2}+b^{2}=c^{2}$
  $a^{2}+4^{2}=5^{2}$
  $a^{2}+16=25$
  $a^{2}+16-16=25-16$
  $a^{2}=9$
  $a=3$
  À ce stade, vous avez tout ce qu'il vous faut pour calculer l'aire du triangle : vous avez les longueurs des deux côtés perpendiculaires (a et b), soit la base et la hauteur. Il ne reste plus qu'à passer à l'application numérique :
  ${\text{Aire}}={\frac {1}{2}}(bh)$
  
  ${\text{Aire}}={\frac {1}{2}}(4)(3)$
  
  ${\text{Aire}}={\frac {1}{2}}(12)$
  
  ${\text{Aire}}=6$
Publicité

Méthode 2

Méthode 2 sur 4:
Calculer l'aire d'un triangle en utilisant les longueurs des côtés

1
Calculez le demi-périmètre du triangle. Comme son nom l'indique, le demi-périmètre d'une figure est la moitié de son périmètre. Avant de trouver le demi-périmètre, il faut calculer le périmètre du triangle en faisant la somme des longueurs de ces trois côtés, ensuite vous multiplierez par ${\frac {1}{2}}$ ${\frac {1}{2}}$ ^{[2]
X
Source de recherche}.
- Prenons le cas d'un triangle dont les trois côtés ont pour mesures 5, 4 et 3 cm. Son demi-périmètre (s) est donné par la formule suivante :
  $s={\frac {1}{2}}(3+4+5)$
  
  $s={\frac {1}{2}}(12)=6$
2
Notez la formule de Héron. La formule est la suivante : ${\text{Aire}}={\sqrt {s(s-a)(s-b)(s-c)}}$ , dans laquelle $s$ est le demi-périmètre du triangle, et $a$ , $b$ et $c$ , les longueurs des trois côtés du triangle ^{[3]
X
Source de recherche}.
3
Faites l'application numérique. Remplacez les lettres de la formule par leurs valeurs respectives. Le danger, s'il existe, consisterait à oublier de remplacer un des $s$ $s$ de la formule.
- Reprenons l'exemple. On a :
  ${\text{Aire}}={\sqrt {s(s-a)(s-b)(s-c)}}$
  ${\text{Aire}}={\sqrt {6(6-3)(6-4)(6-5)}}$
4
Calculez ce qui est entre parenthèses. Vous avez trois opérations à faire, celles qui consistent à ôter au demi-périmètre chacun des trois côtés. Cela fait, faites le produit de ces trois résultats.
- Si l'on reprend notre exemple, on a :
  ${\text{Aire}}={\sqrt {6(6-3)(6-4)(6-5)}}$
  ${\text{Aire}}={\sqrt {6(3)(2)(1)}}$
  ${\text{Aire}}={\sqrt {6(6)}}$
5
Multipliez les valeurs sous la racine. Calculez ensuite la racine carrée de ce résultat et vous aurez l'aire du triangle en unités carrées.
- Si l’on reprend notre exemple, on a :
  ${\text{Aire}}={\sqrt {6(6)}}$
  ${\text{Aire}}={\sqrt {36}}$
  ${\text{Aire}}=6$
  En conséquence, l'aire du triangle est de 6 cm².
Publicité

Méthode 3

Méthode 3 sur 4:
Calculer l'aire d'un triangle équilatéral en utilisant un seul côté

1
Trouvez la longueur d'un des côtés du triangle. Par définition, un triangle équilatéral est un triangle qui a trois côtés égaux. Partant de là, si vous obtenez la mesure d'un des côtés, vous les avez toutes les trois, puisqu'elles sont identiques ^{[4]
X
Source de recherche}.
- Pour illustrer notre propos, prenons l'exemple d'un triangle équilatéral de 6 cm de côté.
2
Posez la formule de calcul de l'aire d'un triangle équilatéral. La formule est la suivante : ${\text{Aire}}=(a^{2}){\frac {\sqrt {3}}{4}}$ , dans laquelle $a$ représente la longueur d'un côté du triangle ^{[5]
X
Source de recherche}.
3
Faites l'application numérique. Remplacez dans la formule le symbole du côté (soit $a$ $a$ ) par sa vraie longueur. Faites d'abord l'élévation de cette valeur au carré.
- Reprenons l'exemple du triangle équilatéral de 6 cm de côté. La formule est la suivante :
  ${\text{Aire}}=(a^{2}){\frac {\sqrt {3}}{4}}$
  
  ${\text{Aire}}=(6^{2}){\frac {\sqrt {3}}{4}}$
  
  ${\text{Aire}}=(36){\frac {\sqrt {3}}{4}}$
4
Multipliez ensuite ce carré par ${\sqrt {3}}$ . Il est préférable d'utiliser la fonction de la racine carrée de votre calculatrice, le résultat sera plus juste. Si vous faites les calculs à la main, prenez 1,732 pour valeur de ${\sqrt {3}}$ ${\sqrt {3}}$ .
- Reprenons l'exemple. On a :
  ${\text{Aire}}=(36){\frac {\sqrt {3}}{4}}$
  
  ${\text{Aire}}={\frac {62,352}{4}}$
5
Divisez le tout par 4. À la suite de cette opération, vous obtenez l'aire du triangle en unités carrées.
- Dans notre exemple, cela donne :
  ${\text{Aire}}={\frac {62,352}{4}}$
  
  ${\text{Aire}}=15,588$
  En conséquence, l'aire d'un triangle équilatéral ayant des côtés de 6 cm de long est d'environ 15,59 cm².
Publicité

Méthode 4

Méthode 4 sur 4:
Calculer l'aire d'un triangle en utilisant les angles

1
Trouvez les mesures de deux côtés adjacents. Il vous faut aussi la mesure de l'angle entre ces deux côtés. Deux côtés sont dits « adjacents » quand ils forment un sommet ^{[6]
X
Source de recherche}. L'angle entre les deux s'appelle « l'angle adjacent ».
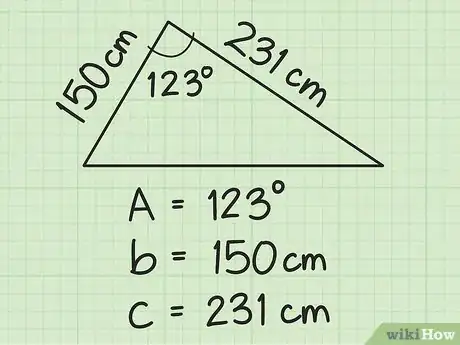
- Prenons l'exemple d'un triangle qui aurait deux côtés adjacents, l'un de 150 cm et l'autre, de 231 cm. On posera que l'angle adjacent (entre les deux) est de 123°.
2
Posez la formule trigonométrique de l'aire du triangle. La formule est la suivante : ${\text{Aire}}={\frac {bc}{2}}\sin({\text{α}})$ , dans laquelle ${\text{b}}$ et ${\text{c}}$ sont deux côtés adjacents du triangle, et ${\text{α}}$ , l'angle adjacent ^{[7]
X
Source de recherche}.
3
Faites l'application numérique. Dans un premier temps, remplacez dans la formule $b$ $b$ et $c$ $c$ par leurs valeurs, multipliez-les, puis divisez le tout par 2.
- Reprenons l'exemple cité ci-dessus. On a :
  ${\text{Aire}}={\frac {bc}{2}}\sin({\text{α}})$
  
  ${\text{Aire}}={\frac {(150)(231)}{2}}\sin({\text{α}})$
  
  ${\text{Aire}}={\frac {(34\ 650)}{2}}\sin({\text{α}})$
  
  ${\text{Aire}}=17\ 325\sin({\text{α}})$
4
Remplacez dans la formule le sinus de l'angle. Pour connaitre la valeur du sinus d'un angle, vous devez utiliser une calculatrice scientifique sur laquelle vous verrez une fonction « sin ». Tapez la mesure de l'angle, puis cette touche.
- Dans notre exemple, le sinus de 123° étant équivalant à 0,83867, la formule devient la suivante :
  ${\text{Aire}}=17\ 325\sin({\text{α}})$
  ${\text{Aire}}=17\ 325(0,83867)$
5
Multipliez ces deux valeurs. En appuyant sur la touche « = », vous obtiendrez l'aire du triangle en unités carrées.
- Reprenons notre exemple. On a :
  ${\text{Aire}}=17\ 325(0,883867)$
  ${\text{Aire}}=14\ 529,96$
  En conséquence, l'aire du triangle en question est d'environ 14 530 cm².
Publicité

Conseils

Si vous ne comprenez pas la formule « base-hauteur », voici quelques explications somme toute simples. Imaginez un second triangle identique qu’on accolerait au premier. Vous obtenez alors soit un rectangle (si vous partez d’un triangle rectangle) soit un parallélogramme (si vous partez d’un triangle quelconque). Or, pour trouver la surface d’un rectangle ou d’un parallélogramme, il suffit de multiplier la longueur par la largeur. Comme vous avez deux triangles identiques dans votre rectangle ou votre parallélogramme, il faut diviser par 2. CQFD !

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Comment calculer la surface d'un triangle

Étapes

Méthode 1

Méthode 1 sur 4:
Calculer l'aire d'un triangle en utilisant la base et la hauteur

Méthode 2

Méthode 2 sur 4:
Calculer l'aire d'un triangle en utilisant les longueurs des côtés

Méthode 3

Méthode 3 sur 4:
Calculer l'aire d'un triangle équilatéral en utilisant un seul côté

Méthode 4

Méthode 4 sur 4:
Calculer l'aire d'un triangle en utilisant les angles

Conseils

wikiHows en relation

Références

À propos de ce wikiHow

Articles en relation

Abonnez-vous à la newsletter gratuite de wikiHow !

Comment calculer la surface d'un triangle

Étapes

Méthode 1 Méthode 1 sur 4:Calculer l'aire d'un triangle en utilisant la base et la hauteur

Méthode 2 Méthode 2 sur 4:Calculer l'aire d'un triangle en utilisant les longueurs des côtés

Méthode 3 Méthode 3 sur 4:Calculer l'aire d'un triangle équilatéral en utilisant un seul côté

Méthode 4 Méthode 4 sur 4:Calculer l'aire d'un triangle en utilisant les angles

Conseils

wikiHows en relation

Références

À propos de ce wikiHow

Articles en relation

Abonnez-vous à la newsletter gratuite de wikiHow !

Méthode 1

Méthode 1 sur 4:
Calculer l'aire d'un triangle en utilisant la base et la hauteur

Méthode 2

Méthode 2 sur 4:
Calculer l'aire d'un triangle en utilisant les longueurs des côtés

Méthode 3

Méthode 3 sur 4:
Calculer l'aire d'un triangle équilatéral en utilisant un seul côté

Méthode 4

Méthode 4 sur 4:
Calculer l'aire d'un triangle en utilisant les angles