Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Il y a 10 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 12 892 fois.
La surface d'un objet plan ou dans l'espace se compose de la somme des surfaces des faces qui le composent. La valeur numérique de cette surface est ce qu'on appelle l'aire de la surface [1] . Concernant les aires de surface des solides, les calculs sont globalement assez simples, à condition de connaitre, et d'employer à bon escient, les bonnes formules de calculs. En fait, dans ce genre de calculs, vous devez commencer par déterminer le nombre et la forme des différentes faces du solide, puis de vous souvenir des formules de calculs des aires associées. Sauf pour des solides très particuliers, vous devriez calculer ces aires sans problèmes.
Étapes
Méthode 1
Méthode 1 sur 7:Calculer l'aire de surface d'un cube
-
1Retenez la formule de calcul de l'aire de surface du cube. Un cube est un solide qui possède six faces carrées absolument identiques. Une face carrée de côté a une aire de : . Comme il y a six faces identiques dans un cube, l'aire totale d'un cube () est égale à : , dans laquelle est, comme cela a été précisé précédemment, aussi bien la longueur que la largeur d'un côté [2] .
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
2Mesurez la longueur d'un des côtés. Comme tous les côtés sont par définition égaux, vous n'avez qu'une seule mesure à faire : mesurez n'importe lequel d'entre eux. Pour la mesure, prenez une règle et soyez précis, ne confondez pas les unités.
- Nous appellerons la mesure du côté d'une face carrée.
- Exemple :
-
3Élevez cette longueur au carré. La mesure que vous venez de faire, vous devez l'élever au carré, c'est-à-dire la multiplier par elle-même. Si c'est plus facile pour vous, vous pouvez retenir la formule équivalente : .
- Nous commençons donc par calculer l'aire d'une des faces du cube.
- Exemple :
-
4Multipliez ce résultat par 6. Souvenez-vous : un cube a six faces carrées absolument identiques. Comme vous venez de calculer l'aire d'une des faces, il ne vous reste plus qu'à multiplier cette dernière par 6.
- À ce stade, commence le calcul de l'aire totale du cube ().
- Exemple :
Publicité
Méthode 2
Méthode 2 sur 7:Calculer l'aire de surface d'un parallélépipède
-
1Retenez la formule de calcul de l'aire de surface du parallélépipède. Comme pour le cube, vous pouvez voir que ce solide a six faces, simplement elles ne sont pas identiques. En fait, les faces sont identiques, mais seulement deux à deux et en position opposée [3] . Partant de cette description, la formule de calcul de l'aire d'un parallélépipède () se présente ainsi : .
- Dans cette formule, est la largeur du parallélépipède, , sa hauteur, et enfin, , sa longueur.
- Si vous décomposez la formule, vous retrouvez bien les trois séries de deux faces identiques, dont les aires sont additionnées pour donner l'aire totale.
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
2Mesurez la longueur, la hauteur et la largeur du parallélépipède. Avec un tel solide, ces trois dimensions sont différentes les unes des autres, aussi devez-vous les mesurer précisément et inscrire les résultats. Bien entendu, toutes ces mesures seront dans la même unité.
- Mesurez la longueur de la base, c'est-à-dire la longueur la plus importante, que nous appellerons .
- Exemple :
- Mesurez la largeur de la base, soit la longueur la plus petite, nous l'appellerons .
- Exemple :
- Mesurez la hauteur du parallélépipède, c'est-à-dire la longueur qui va du bas du solide au sommet et nous l'appellerons .
- Exemple :
-
3Calculez l'aire de la face inférieure () du parallélépipède. Vous la multiplierez par 2, car il y a deux faces de ce type, en position opposée. Pour la face de dessous, multipliez la longueur par la largeur, soit par . La face opposée, soit supérieure (), a la même aire, d'où la nécessité de multiplier par 2 [4] .
- Exemple :
-
4Calculez l'aire de la face de côté () du parallélépipède. Là encore, vous devez la multiplier par 2, car il y a une même face opposée. Pour la face du côté gauche, multipliez la largeur par la hauteur, soit par . La face opposée, soit la face du côté droit (), a la même aire, d'où la nécessité de multiplier par 2 [5] .
- Exemple :
-
5Calculez l'aire de la face avant. Comme précédemment, vous avez deux faces identiques, celle du devant () et celle de derrière (). Multipliez la longueur par la largeur, soit par . Pour terminer, multipliez ce résultat par 2 [6] .
- Exemple :
-
6Additionnez ces trois aires. Vous avez calculé les aires des faces opposées et vous avez donc ainsi fait le tour de toutes les faces, sans en oublier une seule : vous devez les additionner pour avoir l'aire de surface totale () du parallélépipède en question [7] .
- Exemple :
Publicité - Exemple :
Méthode 3
Méthode 3 sur 7:Calculer l'aire de surface d'un prisme triangulaire
-
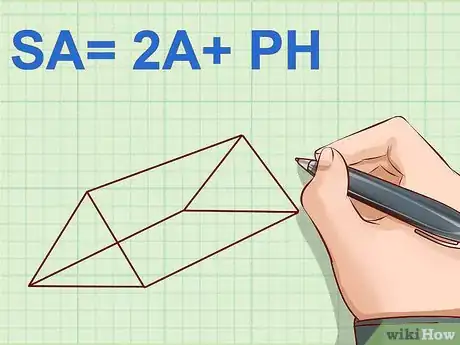
1Retenez la formule de calcul de l'aire de surface du prisme triangulaire. Un tel polyèdre a deux faces triangulaires, qui sont parallèles et de mêmes dimensions, et trois faces rectangulaires. Il vous faut donc trouver les aires de ces cinq faces et l'additionner. La formule peut être simplifiée sous la forme : , formule dans laquelle est l'aire d'une des bases triangulaires, , le périmètre de la base triangulaire et , la hauteur du prisme.
- Dans cette formule, est l'aire d'un des deux triangles, dont la formule est : , étant la base du triangle et , sa hauteur associée.
- est le périmètre d'un des triangles identiques, c'est-à-dire la somme des longueurs de ses trois côtés.
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
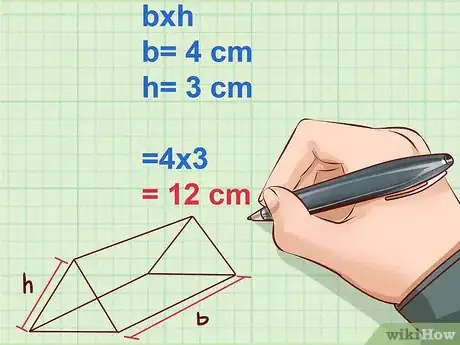
2Calculez d'abord l'aire d'une des faces triangulaires. Multipliez ensuite ce résultat par 2. Comme cela a été dit, l'aire d'un triangle s'obtient avec la formule : , dans laquelle est une base du triangle et , sa hauteur associée. Comme il y a deux faces du même type, il faudra multiplier le résultat par 2, ce qui fait que la formule de l'aire des deux triangles est en fait : .
- La base () est une des longueurs du triangle, celle que vous voulez.
- Exemple :
- La hauteur () de cette même base est la longueur qui va du sommet opposé à la base et coupe cette dernière à angle droit.
- Exemple :
- L'aire des deux triangles de base est donc :
.
-
3Mesurez le périmètre d'un des triangles. Pour cela, mesurez précisément chacun des côtés, puis additionnez-les. Mesurez également la hauteur () du prisme, cette dimension est la longueur qui va d'une face triangulaire à l'autre.
- Exemple :
- Si les trois sommets du triangle s'appellent , et , mesurez et .
- Exemple :
-
4Calculez le périmètre () du triangle. Celui s'obtient simplement en additionnant les longueurs des côtés mentionnés plus haut, soit .
- Exemple :
-
5Multipliez ce périmètre par la hauteur du prisme. Pour mémoire, cette dernière est la longueur qui va d'une face triangulaire à l'autre. À ce stade, multipliez par .
- Exemple :
-
6Faites la somme des deux aires. Elle consiste à ajouter à l'aire des bases (2 faces) et l'aire latérale du prisme (3 faces) : vous obtenez alors l'aire totale du solide en question.
- Exemple :
Publicité
Méthode 4
Méthode 4 sur 7:Calculer l'aire de surface d'une sphère
-
1Retenez la formule de calcul de l'aire de surface d'une sphère. Une sphère est un solide dont la surface est constituée de tous les points à égale distance d'un centre. Son calcul suppose d'utiliser la constante mathématique . La formule de l'aire de surface () d'une sphère est la suivante : [8] .
- Dans cette formule, est le rayon de la sphère. Généralement, vous prendrez 3,14 comme valeur arrondie de .
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
2Mesurez le rayon de la sphère. Le rayon (), égal à la moitié du diamètre, est la longueur qui va du centre du cercle à un des points de la surface de la sphère [9] .
- Exemple :
-
3Élevez le rayon au carré. Pour élever un nombre au carré, il suffit de le multiplier par lui-même. Si vous le voulez, vous pouvez récrire la formule sous la forme : [10] .
- Exemple :
-
4Multipliez ce résultat par π. Cette dernière constante est en fait le rapport de la circonférence d'un cercle à son diamètre et vaut environ 3,14 [11] . C'est un nombre irrationnel dont l'écriture décimale n’est ni finie, ni périodique, c'est pourquoi on l'arrondit souvent par commodité à 3,14. Multipliez le rayon au carré par 3,14 et vous obtenez l'aire du disque optimal de la sphère [12] .
- Exemple :
-
5Multipliez ce résultat par 4. Pour finir, multipliez le résultat trouvé par 4. Il est trop compliqué d'expliquer ici pourquoi il faut multiplier par 4, mais, ce faisant, vous obtiendrez l'aire de la surface de votre sphère [13] .
- Exemple :
Publicité
Méthode 5
Méthode 5 sur 7:Calculer l'aire de surface d'un cylindre
-
1Retenez la formule de calcul de l'aire de surface du cylindre. Un cylindre se compose de deux bases circulaires identiques et opposées, reliées par une surface rectangulaire. La formule de calcul de l'aire totale () du cylindre se présente comme suit : , formule dans laquelle est le rayon de la base circulaire, , la hauteur du cylindre et , la constante bien connue, dont la valeur arrondie est 3,14 [14] .
- représente l'aire de surface des deux bases circulaires, tandis que est l'aire de la surface latérale du cylindre.
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
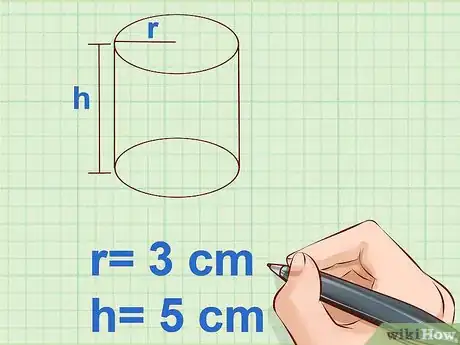
2Mesurez le rayon et la hauteur du cylindre. Le rayon (), égal à la moitié du diamètre, est la longueur qui va du centre du cercle à un des points du cercle [15] . La hauteur () est, quant à elle, la longueur qui va d'un cercle à l'autre. Servez-vous d'une règle pour ces mesures et soyez précis.
- Exemple :
- Exemple :
-
3Calculez le double de l'aire de la base. La base du cylindre (il y en a deux, en fait) est un cercle, sa surface s'obtient en appliquant la formule : . Mesurez le rayon, élevez-le au carré (vous le multipliez par lui-même), puis multipliez le résultat obtenu par . Comme il y a deux cercles, vous devez encore multiplier par 2 [16] .
- Exemple : (une base circulaire)
- Exemple : (les deux bases circulaires)
-
4Calculez l'aire latérale du cylindre. C'est la surface qui unit les deux cercles de base. c'est en fait un rectangle dont la largeur est le périmètre du cercle, et la longueur, la hauteur du cylindre. La formule est donc : . Les opérations sont simples : vous multipliez le rayon par 2, puis par et enfin, par la hauteur [17] .
- Exemple :
-
5Faites la somme des surfaces. Additionnez l'aire des deux faces circulaires et celle de l'aire latérale. La formule de calcul, , reflète bien ces deux aires [18] . Par expérience, il a été remarqué que le calcul de l'aire de surface d'un cylindre amène des erreurs, aussi faites très attention.
- Exemple :
Publicité
Méthode 6
Méthode 6 sur 7:Calculer l'aire de surface d'une pyramide à base carrée
-
1Retenez la formule de l'aire de surface d'une pyramide à base carrée. Une telle pyramide a donc une base carrée et quatre faces triangulaires. Pour rappel, l'aire d'un carré s'obtient en multipliant le côté du carré par lui-même. Quant à l'aire d'un triangle, elle est calculée avec la formule : , étant une des bases du triangle et , sa hauteur associée. Comme vous avez quatre faces triangulaires, vous allez tout logiquement devoir multiplier par 4 pour avoir la surface des quatre faces. Si vous y ajoutez l'aire de la base carrée (), vous obtenez l'aire totale de la pyramide. La formule se présente comme suit : [19] .
- Dans cette formule, est le côté du carré qui forme la base de la pyramide et est la hauteur d'un des triangles latéraux, laquelle se trouve être également ce qu'on appelle « l'apothème » de la pyramide.
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
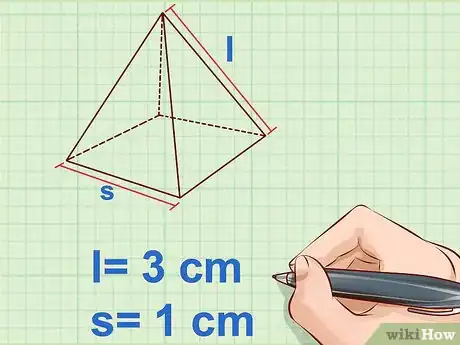
2Mesurez l'apothème et le côté de la base carrée. L'apothème () est la pente de la pyramide, ce segment qui va du sommet de la pyramide à la base, coupant au passage cette dernière à angle droit. Mesurez aussi la longueur () du côté de la base carrée de la pyramide, utilisez une règle et soyez précis dans vos mesures. Il est inutile de mesurer l'autre côté, puisque la base est carrée [20] .
- Exemple :
- Exemple :
-
3Calculez l'aire de la base carrée. Pour cela, il suffit d'élever au carré la longueur du côté, ou si vous préférez, de la multiplier par elle-même [21] .
- Exemple :
-
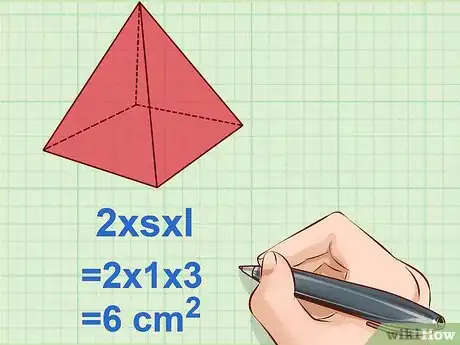
4Calculez l'aire totale des quatre faces triangulaires. Ce que vous calculez ici, c'est en fait l'aire latérale () de la pyramide, composée de quatre triangles égaux. La formule est la suivante : , étant le côté de la base carrée et , l'apothème de la pyramide. Le fait de multiplier par 2 donne l'aire latérale [22] .
- Exemple :
-
5Faites la somme des surfaces. Additionnez l'aire de la base de la pyramide et celle de la surface latérale : vous obtenez l'aire totale de la pyramide [23] .
- Exemple :
Publicité
Méthode 7
Méthode 7 sur 7:Calculer l'aire de surface d'un cône
-
1Retenez la formule de l'aire de surface d'un cône. Un tel solide est composé d'une base circulaire et d'une surface latérale qui finit en un point au-dessus de la base. Pour calculer son aire de surface totale, vous devez d'abord calculer celle de la base circulaire, puis celle de la surface latérale, vous additionnerez ensuite les deux. La formule de calcul est donc la suivante : , formule dans laquelle est le rayon de la base circulaire, , l'apothème du cône, et , la constante bien connue, dont la valeur approchée est 3,14 [24] .
- Les unités d'aire de surface sont des unités de longueur élevées au carré : mm2, cm2, m2, etc.
-
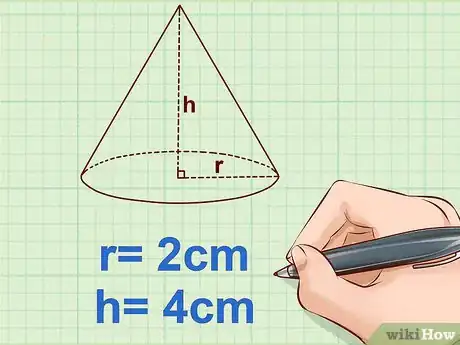
2Mesurez le rayon et la hauteur du cône. Le rayon () est la longueur qui va du centre du cercle à un des points du cercle. La hauteur () est, quant à elle, la longueur qui va du sommet du cône au centre de la base [25] . Le erreurs de mesure s'expliquent par une mauvaise localisation du centre.
- Exemple :
- Exemple :
-
3Calculez l'apothème () du cône. L'apothème d'un cône est en fait l'hypoténuse d'un triangle dont les côtés sont le sommet du cône, le centre de la base et un point du cercle de base. Vous devez donc utiliser le théorème de Pythagore. La formule de calcul est la suivante : , formule dans laquelle est le rayon et , la hauteur du cône [26] .
- Exemple :
-
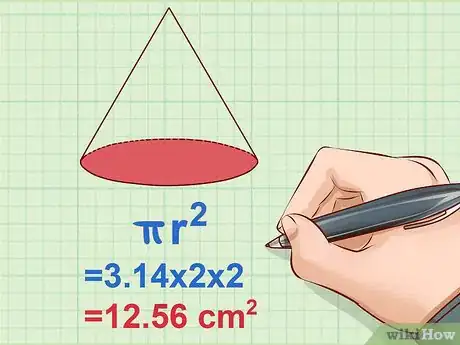
4Déterminez l'aire de la base circulaire. Comme la base est un cercle, la formule de l'aire est la suivante : . Après avoir mesuré le rayon, vous l'élevez au carré (vous le multipliez par lui-même), puis vous multipliez le résultat obtenu par [27] .
- Exemple :
-
5Calculez l'aire latérale du cône. Servez-vous de la formule suivante : , dans laquelle est le rayon du cercle et , l'apothème obtenu précédemment. Multipliez les trois éléments et vous aurez la surface latérale [28] .
- Exemple :
-
6Faites la somme des deux aires. Pour obtenir le résultat escompté, il ne vous reste donc qu'à additionner ces deux dimensions. Prenez garde que votre résultat soit cohérent [29] .
- Exemple :
Publicité
Éléments nécessaires
- Une règle
- Un stylo ou un crayon
- Du papier
Références
- ↑ http://www.math.com/tables/geometry/surfareas.htm
- ↑ http://www.math.com/tables/geometry/surfareas.htm
- ↑ http://www.aaamath.com/geo79_x9.htm
- ↑ http://www.aaamath.com/geo79_x9.htm
- ↑ http://www.aaamath.com/geo79_x9.htm
- ↑ http://www.aaamath.com/geo79_x9.htm
- ↑ http://www.aaamath.com/geo79_x9.htm
- ↑ http://www.mathopenref.com/spherearea.html
- ↑ http://www.mathgoodies.com/lessons/vol2/circumference.html
- ↑ http://www.mathopenref.com/spherearea.html
- ↑ https://www.mathsisfun.com/definitions/pi.html
- ↑ http://www.mathopenref.com/spherearea.html
- ↑ http://www.mathopenref.com/spherearea.html
- ↑ http://www.aaamath.com/exp79x10.htm
- ↑ http://www.mathgoodies.com/lessons/vol2/circumference.html
- ↑ http://www.aaamath.com/exp79x10.htm
- ↑ http://www.aaamath.com/exp79x10.htm
- ↑ http://www.aaamath.com/exp79x10.htm
- ↑ http://www.basic-mathematics.com/surface-area-of-a-square-pyramid.html
- ↑ http://www.basic-mathematics.com/surface-area-of-a-square-pyramid.html
- ↑ http://www.basic-mathematics.com/surface-area-of-a-square-pyramid.html
- ↑ http://www.basic-mathematics.com/surface-area-of-a-square-pyramid.html
- ↑ http://www.basic-mathematics.com/surface-area-of-a-square-pyramid.html
- ↑ http://www.web-formulas.com/Math_Formulas/Geometry_Surface_of_Cone.aspx
- ↑ http://www.web-formulas.com/Math_Formulas/Geometry_Surface_of_Cone.aspx
- ↑ http://www.web-formulas.com/Math_Formulas/Geometry_Surface_of_Cone.aspx
- ↑ http://www.web-formulas.com/Math_Formulas/Geometry_Surface_of_Cone.aspx
- ↑ http://www.web-formulas.com/Math_Formulas/Geometry_Surface_of_Cone.aspx
- ↑ http://www.web-formulas.com/Math_Formulas/Geometry_Surface_of_Cone.aspx










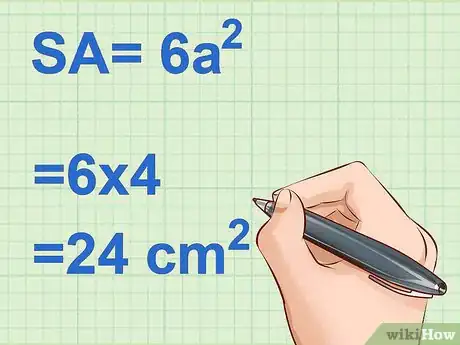










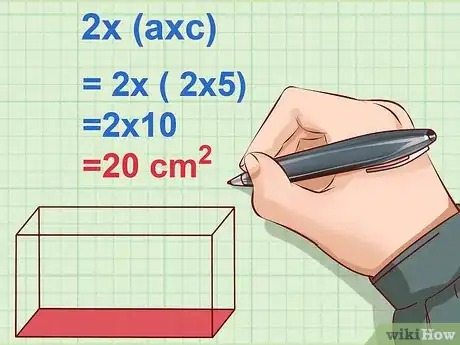



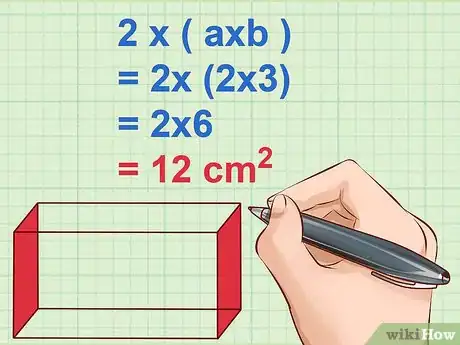



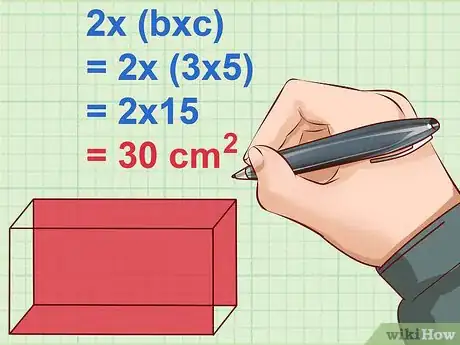



































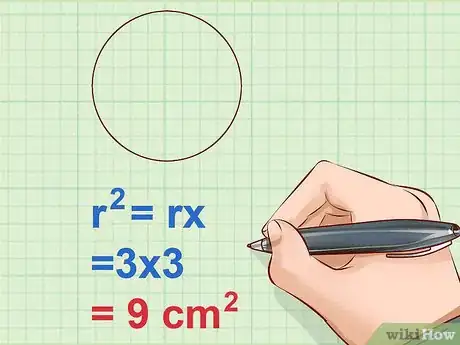























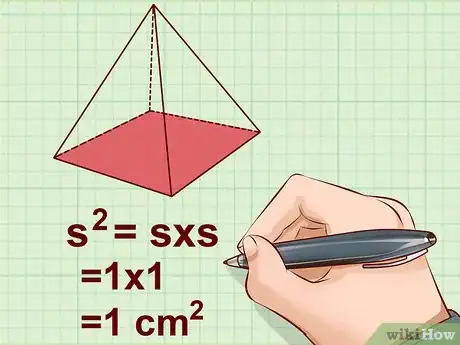




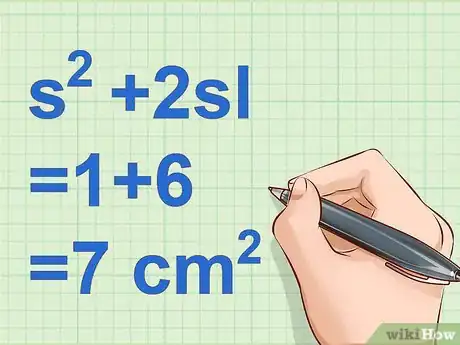

































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 12 892 fois.