Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 84 551 fois.
En matière statistique, la fréquence absolue d'une valeur est simple à trouver : elle consiste à compter le nombre d'occurrences de cette valeur dans un échantillon (de personnes, d'objets…). La fréquence relative est un peu plus complexe dans la mesure où elle mesure la fréquence d'une valeur, exprimée en tant que proportion d'un tout. On la calcule en divisant la fréquence absolue par la taille de l'échantillon, ce dernier portant le nom de population. Afin de rendre plus facile le calcul de la fréquence relative, il faut classer les données, faire quelques calculs simples, puis dresser un tableau de fréquence.
Étapes
Partie 1
Partie 1 sur 3:Préparer les données pour le calcul de la fréquence relative
-
1Récupérez des données. À moins qu'on ne vous les donne d'entrée de jeu, dans un exercice par exemple, vous allez devoir par l'expérience, récolter vos données. Qu'il s'agisse de poids, de taille, d'années…, ce sera à vous de déterminer au départ le degré de précision de vos mesures.
- Pour mieux comprendre, prenons l'exemple de personnes qui sont allées voir un film donné. Vous ferez le relevé des âges de chaque spectateur. Si c'est un film tout public, vous aurez des personnes entre 10 et 70 (ou 80) ans, soit 60 à 70 âges différents. Vous pouvez regrouper vos spectateurs en six classes : moins de 20 ans, 20 à 29 ans, 30 à 39 ans, 40 à 49 ans, 50 à 59 ans et plus de 60 ans. Ce regroupement en classes est plus pratique.
- Comme autre exemple, on peut prendre l'hypothèse d'un médecin qui prendrait la température de tous ses patients sur une journée. S'il décide de prendre des températures entières (37 °C, 38 °C…), ce ne sera pas pertinent : il faut alors noter les températures au dixième (37,2 °C, 37,3 °C…).
-
2Triez vos données. Si c'est vous qui faites l'observation et les relevés, vous allez obtenir une série de données, une « population » qui se présente, par exemple, ainsi : 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. De quoi y perdre son latin ! Il n'y a aucune logique, aucun classement, ce sont des données brutes. Il faut les trier par ordre croissant, ce qui donne : 1, 1, 1, 2, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 7.
- Si les séries sont composées de valeurs proches les unes des autres, veillez à n'en oublier aucune que ce soit en triant ou en les récrivant. Recomptez vos valeurs pour vérifier que vous n'en avez pas oublié.
-
3Mettez vos données sous forme de tableau. Vous pouvez regrouper toutes vos données et vos calculs en dressant un tableau de fréquences. Vous ferez un tableau à trois colonnes dans lequel vous mettrez les fréquences relatives. Intitulez vos colonnes comme suit [1] .
- : dans cette colonne, vous mettrez toutes les valeurs différentes de votre série. Il n'est plus question de les mettre toutes. Ainsi, même si le 4 apparait plusieurs fois dans votre série, vous ne mettrez qu'une seule fois cette valeur dans la première colonne.
- : en statistiques, cette appellation correspond à l'effectif de la valeur , c'est-à-dire le nombre de fois où la valeur apparait, étant l'effectif total. L'expression se prononce « n de i ». Cependant le plus souvent, cette colonne est intitulée « Effectifs ». C'est dans cette colonne que vous consignerez le nombre de fois où la valeur de la colonne précédente apparait. Ainsi, si la valeur 4 apparait trois fois dans la série, vous mettrez un 3 sur la même ligne que le 4, mais à droite.
- : en statistiques, cette appellation correspond à la fréquence relative et se lit « fréquence de i ». Chacune des valeurs de cette colonne s'obtient en utilisant les valeurs de la colonne précédente et celle de l'effectif total. Ces valeurs peuvent être données sous forme des chiffres décimaux ou de pourcentages, comme on va le voir à présent.
Publicité
Partie 2
Partie 2 sur 3:Calculer des fréquences relatives
-
1Trouvez l'effectif total de votre série. La fréquence relative mesure la proportion de la présence d'une valeur dans une série de données. Pour calculer une fréquence relative, vous devez impérativement connaitre la taille (ou l'effectif) de votre série, c'est-à-dire le nombre de valeurs qui la compose. Cette taille sera le dénominateur de la fraction qui permet de calculer la fréquence [2] .
- Si l'on reprend l'exemple précédent, on voit que la série a un effectif total de 16 données.
-
2Calculez les effectifs de chaque valeur. On parle aussi de « taille » de la valeur. Vous devez recenser le nombre de fois qu'une valeur apparait dans l'échantillon. Partant de là, vous pourrez calculer la fréquence relative d'une valeur particulière ou celles de toutes les valeurs de l'échantillon [3] .
- Reprenons l'exemple précédent et intéressons-nous à la valeur 4 : on voit qu'elle apparait 3 fois dans la série, c'est là son effectif.
-
3Divisez l'effectif de la valeur par l'effectif de la série. Le terme « effectif » peut remplacé par celui de « taille ». Ce sont les premiers et les derniers calculs à faire pour remplir la dernière colonne, celle des fréquences relatives. Pour cela, vous pouvez laisser les fréquences sous forme de fractions, les calculer avec une calculatrice ou, si vous utilisez un tableur, programmer les cellules de cette dernière colonne [4] .
- Reprenons l'exemple précédent. La valeur apparait donc trois fois et l'effectif de la série est de 16 : vous pouvez en déduire que la fréquence relative de cette valeur est de 3/16, ce qui, après calcul au dix-millième, donne 0,1875, comme on le voit sur le tableau.
Publicité
Partie 3
Partie 3 sur 3:Bien présenter des fréquences relatives
-
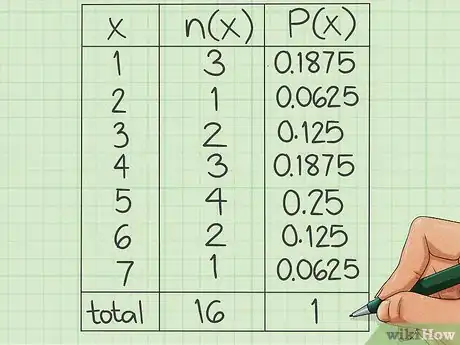
1Présentez vos résultats dans un tableau de fréquences. Si vous faites vos calculs à part, il est bon de présenter vos résultats dans le tableau de fréquences qui est déjà partiellement rempli. Vous gagnerez en lisibilité. Après chaque calcul, inscrivez sur la bonne ligne et dans la troisième colonne, la fréquence trouvée. En général, on donne le résultat sous la forme d'un chiffre à deux décimales, mais il est possible qu'on vous donne une autre consigne. Une fois les calculs faits, vérifiez que la somme des fréquences fasse 1 ou quelque valeur approchante (à cause des arrondissements) [5] .
- Après calculs et arrondissements, vous allez obtenir le tableau des fréquences relatives suivant :
- i : n(i) : f(i)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Total : 16 : 1,01
-
2Indiquez les valeurs non présentes dans la série. Dans certains échantillons, il peut y avoir des valeurs non présentes. Si vous lancez deux dés, il est possible que le 3 ne sorte pas sur 25 lancers. Si c'est le cas, cette valeur 3 est sortie 0 fois, vous pouvez l'indiquer dans votre tableau en mettant un 0 comme n(i) et donc 0,00 dans f(i).
- Dans l'exemple que nous avions pris, toutes les valeurs de 1 à 7 étaient présentes dans la série, mais admettons que le 3 ait été absent, sur la ligne du 3 vous mettriez alors en effectif la valeur 0 et la fréquence relative serait alors aussi de 0 (0/16).
-
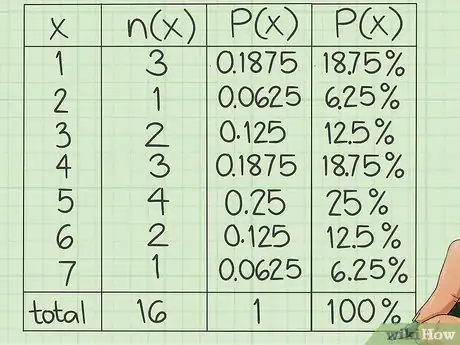
3Présentez vos résultats sous forme de pourcentages. Il est possible qu'on vous demande de présenter les fréquences sous forme de pourcentages, c'est d'ailleurs souvent comme cela que cela se passe. Il est plus facile de visualiser un pourcentage qu'un chiffre décimal entre 0 et 1. Pour convertir une valeur décimale en pourcentage, il suffit de la multiplier par 100, sans oublier d'ajouter à droite le symbole du pourcentage (%).
- Transformé en pourcentage, 0,13 devient 13 % (13/100).
- Transformé en pourcentage, 0,06 devient 6 % (faites attention avec les zéros intercalaires).
Publicité
Conseils
- Concrètement, une fréquence relative donne une indication sur la fréquence d'apparition d'un évènement dans une série d'évènements.
- La somme de toutes les fréquences relatives des valeurs (ou des classes) d'une série doit être égale à 1. Comme vous avez parfois arrondi certaines valeurs, il est possible que vous n'obteniez pas exactement cette valeur de 1, mais une valeur très proche.
- Si vous avez de grands échantillons, il est certainement plus rapide et plus sûr d'utiliser des logiciels de manipulation de données numériques, comme MS Excel ou MATLAB… à condition de bien programmer les cellules.
Références
- ↑ http://www.zweigmedia.com/RealWorld/tutorialsf15e/frames6_2.html
- ↑ http://www.zweigmedia.com/RealWorld/tutorialsf15e/frames6_2.html
- ↑ http://www.zweigmedia.com/RealWorld/tutorialsf15e/frames6_2.html
- ↑ http://www.zweigmedia.com/RealWorld/tutorialsf15e/frames6_2.html
- ↑ http://www.zweigmedia.com/RealWorld/tutorialsf15e/frames6_2.html

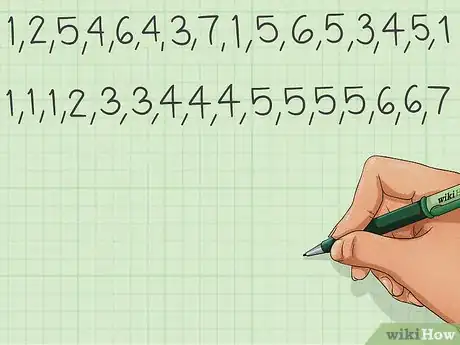
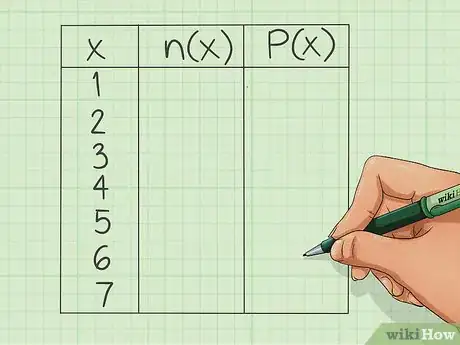




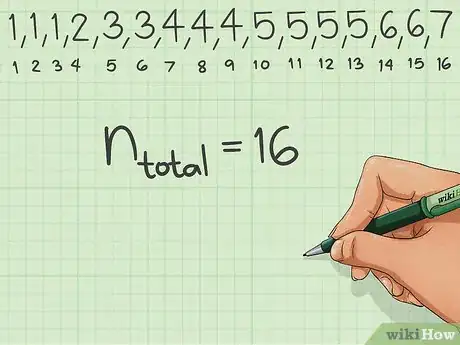
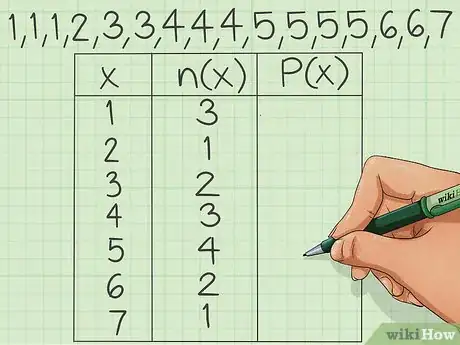


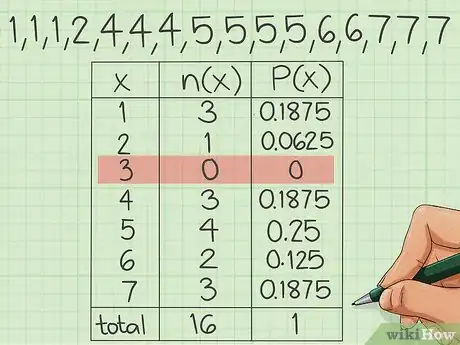



















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 84 551 fois.