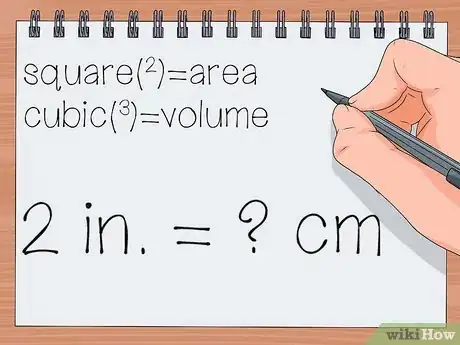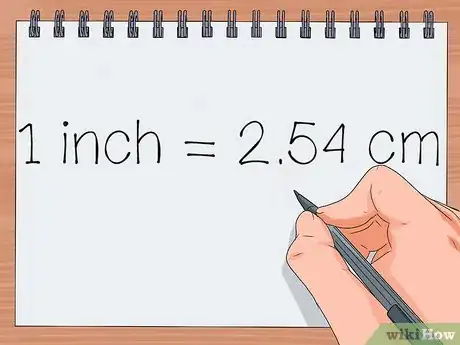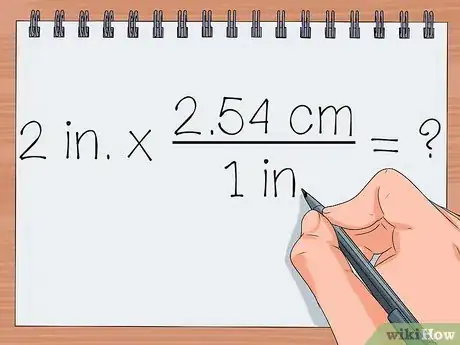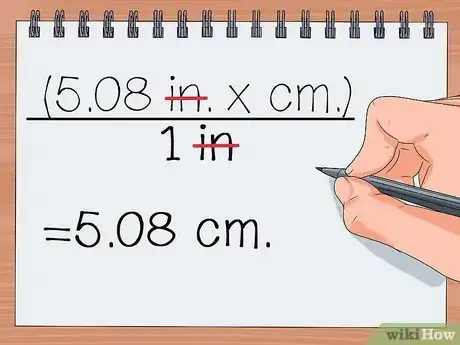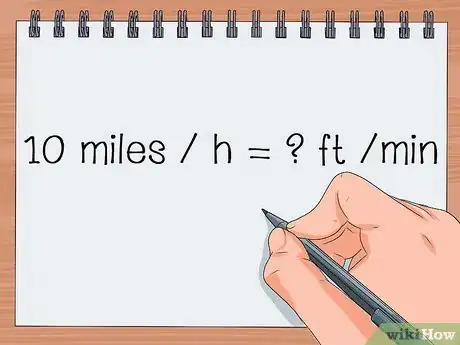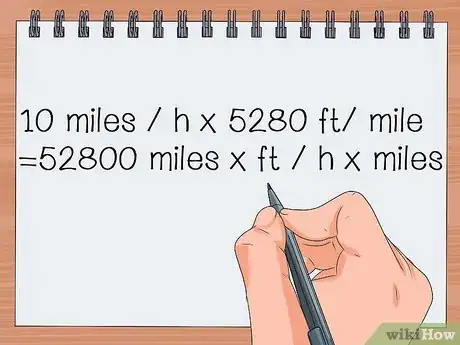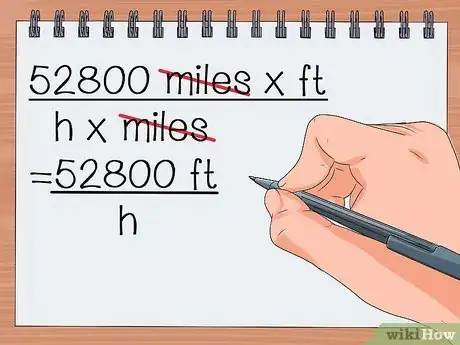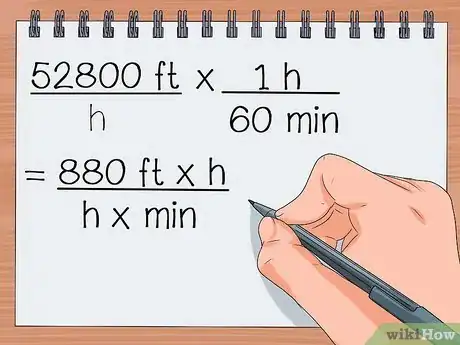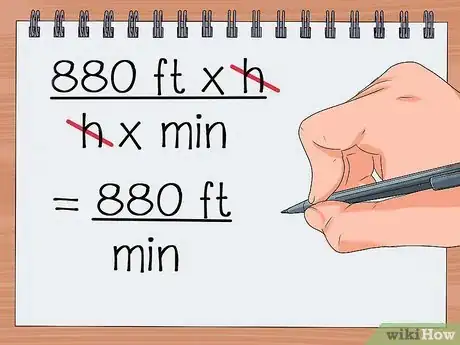Comment convertir des unités de mesure

Avec tous les systèmes de mesure existants, savoir convertir des unités d'un système dans un autre peut s'avérer utile. À moins que vous ne manipuliez que des unités appartenant à un système décimal (système métrique, par exemple), il vous faudra savoir opérer avec des fractions de conversion. Quoi qu'il en soit, quand vous convertissez des unités de mesure, il ne faut jamais perdre de vue, au cours de vos calculs, les unités.

Méthode 1
Méthode 1 sur 3:
Convertir des unités de mesure (système non décimal)

  1. Image intitulée Convert Units Step 1
    1
    Comparez vos deux unités. Les deux unités en jeu doivent mesurer une même dimension. Ainsi, si on vous demande de convertir 2 pouces (2 po) en centimètres, l'exercice est cohérent dans la mesure où les pouces et les centimètres sont deux mesures de longueur. Si l'on vous donne deux unités radicalement différentes (une de longueur et une de poids), il est impossible de convertir de l'une vers l'autre.
    • Certaines personnes mélangent les longueurs, les surfaces, les volumes… Dès qu'on a des unités « carrées » (m2), on a affaire à des surfaces. Quand il s'agit d'unités « cubiques » (cm3), on est face à des volumes.
    • Pour reprendre l'exercice donné plus haut, il est cohérent d'écrire : 2 po = x cm.
  2. Image intitulée Convert Units Step 2
    2
    Ayez le facteur de conversion. Avant de vous lancer dans quelque calcul que ce soit, vous devez connaitre le rapport mathématique entre les deux unités. Si ce facteur est un nombre décimal un peu long, il est souvent utile de l'arrondir. Si vous ne savez pas ce qu'est un chiffre significatif, ne prenez que les deux ou trois premières décimales.
    • Ainsi, pour convertir 2 pouces en centimètres, vous devez impérativement savoir que : 1 pouce = 2,54 centimètres.
  3. Image intitulée Convert Units Step 3
    3
    Présentez ce rapport de conversion sous forme de fraction. Les unités doivent impérativement apparaitre. L'unité de départ sera sous le trait de fraction (en dénominateur) et celle d'arrivée, au-dessus du trait (en numérateur) [1] .
    • Ainsi, inscrivez 2,54 cm/1 po. Cette fraction pourrait se lire : « 2,54 centimètres par pouce ».
  4. Image intitulée Convert Units Step 4
    4
    Posez bien le problème. Avec la fraction de conversion, vous pouvez convertir en centimètres n'importe quelle valeur en pouces : vous multipliez la valeur à convertir par cette fraction. Posez l'opération en notant les unités, c'est important !
    • 2 po x (2,54 cm/1 po) = x
  5. Image intitulée Convert Units Step 5
    5
    Faites la multiplication. À chaque étape du calcul, vous devez faire apparaitre les unités.
    • 2 po x (2,54 cm/1 po)
    • = (2 po x 2,54 cm)/1 po
    • = (5,08 po x cm)/ po
  6. Image intitulée Convert Units Step 6
    6
    Simplifiez les unités identiques. Si une unité apparait à la fois en numérateur et en dénominateur, supprimez-la en haut et en bas. L'unité restante est l'unité de la réponse.
    • (5,08 po x cm)/po
    • = 5,08 cm
  7. Image intitulée Convert Units Step 7
    7
    Procédez à des vérifications. Si vous n'arrivez pas à simplifier une des unités, c'est que vous êtes trompé quelque part. Vérifiez l'ordre de vos fractions.
    • Admettons que vous ayez posé le produit suivant : 2 po x (1 po / 2,54 cm), soit (2 po x 1 po) / 2,54 cm. Vous vous retrouvez avec « (po x po) » en numérateur et « cm » en dénominateur. Il est impossible de simplifier par « po ». Ici, il fallait inverser la fraction de conversion et écrire : 2 po x (2,54 cm / 1 po).
    Publicité

Méthode 2
Méthode 2 sur 3:
Convertir des valeurs présentant plusieurs unités (systèmes non décimaux)

  1. Image intitulée Convert Units Step 8
    1
    Inscrivez correctement les données du problème. Lisez bien l'énoncé et posez bien le problème.
    • Exercice : Un vélo se déplace à une vitesse moyenne de 10 miles à l'heure, quelle distance, en pieds, parcourra-t-il en une minute ?
    • Le problème peut s'écrire ainsi : 10 miles / heure = x pieds / minute ou 10 mi / h = x pi / min, x étant la distance à découvrir.
  2. Image intitulée Convert Units Step 9
    2
    Trouvez le facteur de conversion d'un groupe d'unités. Pour rappel, on ne peut convertir qu'entre unités d'une même dimension. Ici, on a des unités de longueur (miles et pieds) et des unités de temps (heures et minutes). On commence donc par convertir le premier groupe d'unités, celui des longueurs.
    • Ainsi, 1 mile = 5 280 pieds.
  3. Image intitulée Convert Units Step 10
    3
    Multipliez votre nombre par la fraction de conversion. Comme cela a été souligné, il faut présenter la fraction de conversion de telle sorte qu'on puisse faire disparaitre une des unités. Quand vous posez la multiplication, n'oubliez jamais de mettre toutes les unités.
    • On a : 10 mi / h (vitesse du vélo) x 5 280 pi / mi (fraction de conversion).
    • Après calcul, on obtient : 52 800 mi x pi / h x mi
  4. Image intitulée Convert Units Step 11
    4
    Simplifiez les unités. Normalement, vous devez avoir une même unité sur et sous le trait de fraction. C'est la condition pour pouvoir simplifier une des unités. Cela fait, ce n'est pas terminé, mais vous avez bien avancé.
    • On simplifie : 52 800 mi x pi / h x mi
    • On obtient alors : 52 800 pi / h
  5. Image intitulée Convert Units Step 12
    5
    Faites de même avec l'autre groupe d'unités. Trouvez le rapport de conversion des autres unités, puis présentez en sorte d'avoir la même unité au-dessus et en dessous du trait de fraction.
    • Reprenons notre exemple : on a résolu la question des longueurs, passons aux unités de temps. Tout le monde sait que : 1 heure = 60 minutes.
    • Pour l'instant, on a la vitesse du vélo : 52 800 pi / h. Comme les heures (h) sont en dénominateur, il faut impérativement avoir des heures en numérateur pour pouvoir simplifier. On prendra donc : 1 heure / 60 minutes.
    • On a : 52 800 pi / h (vitesse du vélo) x 1 h / 60 min (fraction de conversion)
    • Après calcul, on obtient : (52 800/60) pi x h / h x min = 880 pi x h / h x min
  6. Image intitulée Convert Units Step 13
    6
    Simplifiez les unités. On a la même unité en haut et en bas : on peut simplifier.
    • On simplifie : 880 pi x h / h x min
    • On obtient alors : 880 pi / min
  7. Image intitulée Convert Units Step 14
    7
    Répétez ces calculs autant de fois que nécessaire. Si vous obtenez les unités demandées, il n'y a plus rien à faire. Si ce n'est pas le cas, convertissez à nouveau jusqu'à avoir les unités réclamées.
    • Quand vous aurez l'habitude, vous pourrez tout mettre sur une seule ligne [2] . Notre exercice aurait pu être présenté ainsi :
    • 10 mi/h x 5 280 pi/mi x 1 h/60 min
    • =10 mi/h x 5 280 pi/mi x 1 h/60 min
    • = 10 x 5 280 pi x 1/60 min
    • = 880 pi / min
    Publicité

Méthode 3
Méthode 3 sur 3:
Convertir des unités du système métrique entre elles

  1. Image intitulée Convert Units Step 15
    1
    Comprenez bien ce qu'est le système métrique (ou système décimal). Dans ce système, les conversions d'une unité à l'autre sont simples. Tout est question de multiples ou de sous-multiples de 10, comme 10, 100, 1 000… ou 0,1, 0,01, 0,001…
  2. Image intitulée Convert Units Step 16
    2
    Connaissez les préfixes des unités. Ce sont eux qui donnent la dimension de l'unité. Nous allons voir des unités de poids, mais les préfixes sont exactement les mêmes pour les longueurs ou les surfaces [3] . Les préfixes sont en italique, les unités commençant par un préfixe en gras sont les plus usitées.
    • kilogramme = 1 000 grammes
    • hectogramme = 100 grammes
    • décagramme = 10 grammes
    • gramme = 1 gramme
    • décigramme = 0,1 gramme (un dixième)
    • centigramme = 0,01 gramme (un centième)
    • milligramme = 0,001 gramme (un millième)
  3. Image intitulée Convert Units Step 17
    3
    Servez-vous de ces préfixes pour vos conversions. Si vous connaissez le sens des préfixes, vous vous éviterez bien des calculs. Voyez plutôt :
    • il est facile de convertir des kilomètres en mètres quand on sait que « kilo » signifie « mille » : 1 kilomètre = 1 000 mètres,
    • il est tout aussi facile de convertir des grammes en milligrammes quand on sait que « milli » signifie « millième partie » : 1 milligramme = 0,001 gramme.
  4. Image intitulée Convert Units Step 18
    4
    Déplacez la virgule. En effet, convertir des unités du système métrique entre elles revient à déplacer une virgule, nul n'est besoin de faire des calculs compliqués. Ainsi, multiplier un nombre par 10 revient à déplacer la virgule (virtuelle ou non) d'un rang vers la droite. À l'inverse, diviser par 10 consiste à déplacer la virgule d'un rang vers la gauche. Prenons un exemple concret :
    • vous devez convertir 65,24 kilogrammes en grammes,
    • vous savez que : 1 kilogramme = 1 000 grammes. Comptez le nombre de zéros, soit trois. Vous devez multiplier votre nombre à convertir par 10 et ce, trois fois de suite, Quand on multiplie à trois reprises par 10, on déplace la virgule de trois rangs vers la droite, ce qui donne :
    • 65,24 x 10 = 652,4 (une fois)
    • 652,4 x 10 = 6 524 (deux fois)
    • 6 524 x 10 = 65 240 (trois fois)
    • La réponse est : 65,24 kilogrammes = 65 240 grammes.
  5. Image intitulée Convert Units Step 19
    5
    Entrainez avec des exercices plus compliqués. Quand les deux unités ont un préfixe différent, il est commode d'opérer en deux temps. On convertit dans l'unité de base (qui n'a pas de préfixe, le gramme dans notre cas), puis on convertit à nouveau dans l'unité demandée. Prenons un exemple concret :
    • vous devez convertir 793 millilitres en décalitres,
    • vous savez que : 1 millilitre = 0,001 litre. Là encore, il y a trois zéros, mais c'est un sous-multiple. Il faut donc déplacer la virgule de trois rangs vers la gauche,
    • 793 millilitres = 793,00 millilitres = 0,793 litre,
    • 10 litres = 1 décalitre, donc 1 litre = 0,1 décalitre. Comme il n'y a qu'un zéro, on déplace la virgule d'un seul rang vers la gauche.
    • La réponse est : 793 millilitres = 0,0793 décalitre.
  6. Image intitulée Convert Units Step 20
    6
    Vérifiez votre résultat. En conversion, il est fréquent de multiplier au lieu de diviser (ou l'inverse). Voyez si votre réponse est logique :
    • si vous convertissez dans une unité supérieure, votre résultat est plus petit (12 pouces deviennent 1 pied),
    • si vous convertissez dans une unité inférieure, votre résultat est plus grand (1 pied devient 12 pouces),
    • si ce principe n'est pas vérifié, refaites vos calculs.
    Publicité

Conseils

  • Des conversions sont parfois nécessaires quand on fait des recettes de cuisine de pays étrangers. Certaines donnent les quantités d'ingrédients en unités de poids (les grammes, en France), d'autres, en unités de volume (« teaspoons, cups… », aux États-Unis, par exemple). Il existe des convertisseurs en ligne qui s'appuient sur les densités des ingrédients pour passer d'un type de mesure à un autre.
Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ https://www.mathsisfun.com/measure/unit-conversion-method.html
  2. ↑ http://www.purplemath.com/modules/units2.htm
  3. ↑ http://www.aaastudy.com/mea212x2.htm

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 11 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 5 867 fois.
Catégories: Mathématiques
Résumé de l'articleX

1. Vérifiez que les deux unités appartiennent bien à la même famille de mesure, par exemple 2 unités de longueur. 2. Trouvez le rapport de conversion entre les deux unités. 3. Notez ce rapport de conversion sous forme d'une fraction, l'unité de départ sera sous le trait de fraction et l'unité que vous convertissez au-dessus du même trait. 4. Multipliez le nombre original par la fraction, en n'oubliant pas d'inscrire les unités (par exemple, mètres et centimètres) de chacun des nombres à chaque étape. 5. Éliminez les unités qui apparaissent aussi bien en haut et en bas de la fraction. 6. Ce qui reste, à savoir un nombre et une unité, est votre nombre converti, avec sa nouvelle unité.

Publicité