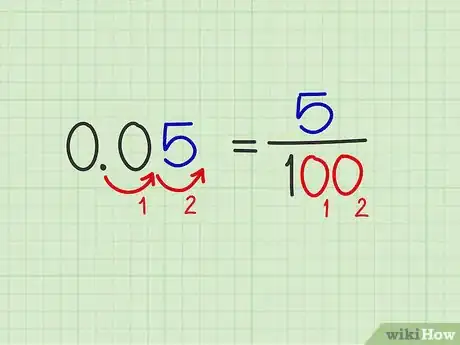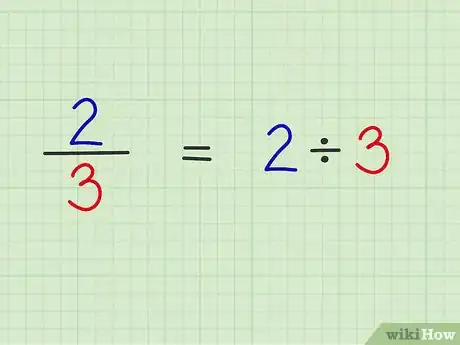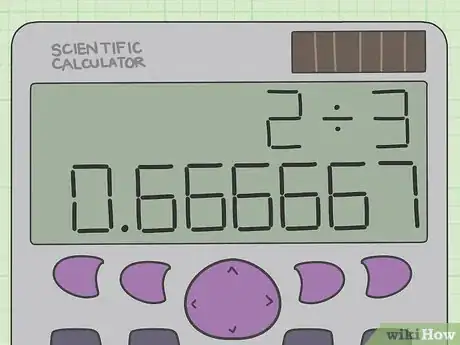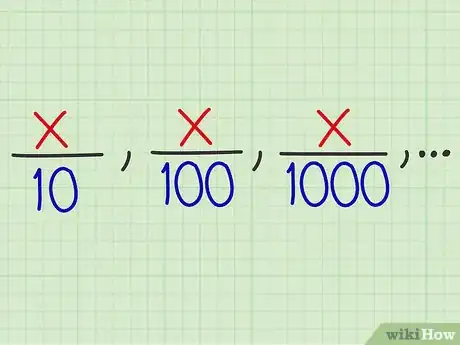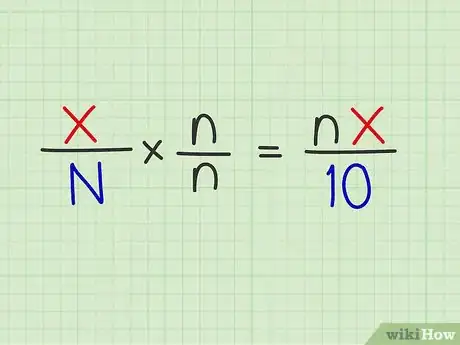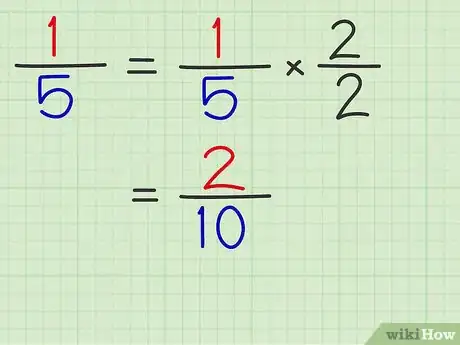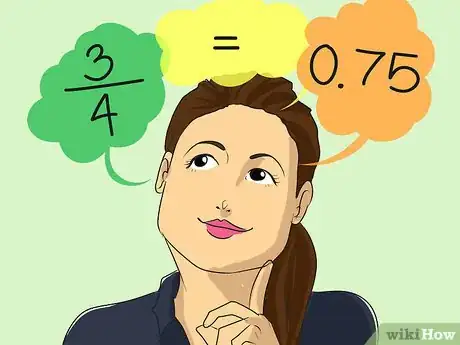Comment convertir les fractions en nombres décimaux

Tout chiffre compris entre 0 et 1 peut s'écrire de deux façons : sous forme de fraction ou de nombre décimal [1] . Ceci est d'ailleurs vrai pour tout chiffre ou nombre. Si tout chiffre compris entre 0 et 1 peut s'écrire sous deux formes, sachez qu'on peut indifféremment passer de l'une à l'autre moyennant quelques formules et quelques calculs.

Partie 1
Partie 1 sur 4:
Quelques généralités sur les fractions et les nombres décimaux

  1. Image intitulée Convert Fractions to Decimals Step 1
    1
    Présentons d'abord une fraction. Elle est composée de trois éléments : un numérateur, situé dans la partie supérieure, un dénominateur, situé dans la partie inférieure et entre les deux, un trait horizontal (ou oblique parfois), le trait de fraction.
    • Le dénominateur représente le nombre de parts équivalentes de l'ensemble de référence. Une pizza, par exemple, peut être coupée en huit parts. Le dénominateur pour la pizza sera donc « 8 ». Si elle avait été coupée en 12 parts, le dénominateur aurait été de « 12 ». La pizza n'a pas changé de taille, simplement elle a été divisée différemment.
    • Le numérateur représente la ou les parts de l'ensemble. Une part de pizza sera représentée par le numérateur « 1 ». Quatre parts seront représentées par le numérateur « 4 ».
  2. Image intitulée Convert Fractions to Decimals Step 2
    2
    Présentons ensuite un nombre décimal. À la différence d'une fraction, un nombre décimal n'a pas de barre de fraction et n'indique pas clairement une part d'un ensemble. Dans un chiffre décimal inférieur à 1, il y a une virgule après un 0 initial (ex. : 0,23). C'est comme si le tout de référence était une puissance de 10 (10, 100, 1 000…) Le nombre de zéros du chiffre décimal précise la taille de la référence de départ.
    • Cependant, les nombres ou les chiffres décimaux peuvent s'exprimer oralement sous la forme d'une fraction. Ainsi, 0,05 peut se dire « zéro - zéro - cinq », mais aussi « cinq-centièmes » (5/100). Dans cette fraction, on retrouve tous les éléments du chiffre : 5 en numérateur et les 2 zéros en dénominateur, précédés du 1, bien sûr !
  3. Image intitulée Convert Fractions to Decimals Step 3
    3
    Quel est alors le lien entre fraction et nombre décimal ? Ces deux formes mathématiques ont en commun de représenter des valeurs comprises entre 0 et 1. En fait, selon les circonstances, on utilisera, après conversion, l'une ou l'autre de ces formes, selon qu'on veut les additionner, les soustraire ou les comparer.
    Publicité

Partie 2
Partie 2 sur 4:
Convertir une fraction en nombre décimal en utilisant une simple division

  1. Image intitulée Convert Fractions to Decimals Step 4
    1
    Pensez la fraction comme une simple division. Pour convertir simplement une fraction en nombre décimal, il suffit de faire une division, celle du numérateur (chiffre ou nombre du haut) par le dénominateur (chiffre ou nombre du bas [2] ).
    • Ainsi, 2/3 n'est rien d'autre que 2 divisé par 3.
  2. Image intitulée Convert Fractions to Decimals Step 5
    2
    Divisez le numérateur de la fraction par son dénominateur. Cette opération, vous pouvez la faire de tête s'ils sont multiples l'un de l'autre, avec une calculatrice ou encore en posant la division sur une feuille de papier.
  3. Image intitulée Convert Fractions to Decimals Step 6
    3
    Vérifiez vos calculs. Multipliez le résultat obtenu, le chiffre décimal, par le dénominateur de la fraction de départ. Vous devez obtenir le numérateur de la même fraction.
    Publicité

Partie 3
Partie 3 sur 4:
Convertir des fractions ayant en dénominateur des puissances de 10

  1. Image intitulée Convert Fractions to Decimals Step 7
    1
    Voyez d'autres cas de conversion de fractions en nombres décimaux. Ainsi, vous comprendrez mieux les relations qui existent entre fractions et nombres décimaux et puis c'est une bonne gymnastique intellectuelle qui vous permettra de progresser en mathématiques !
  2. Image intitulée Convert Fractions to Decimals Step 8
    2
    Voyons par exemple ce qu'est un dénominateur de puissance 10. Il s'agit simplement d'un dénominateur qui est une « puissance de 10 », pour faire court un multiple de 10, comme 1 000 (103) ou 1 000 000 (106). En cours de mathématiques, à l'école, on rencontre le plus souvent 10 (101), 100 (102), voire 1 000.
  3. Image intitulée Convert Fractions to Decimals Step 9
    3
    Apprenez à repérer des fractions qui seront facilement transformables en fractions avec dénominateurs en puissance de 10. Tout dénominateur égal à 5, 10, 25 ou 50 sera très facile à convertir en puissance de 10, puis en nombre décimal. Ce sera encore plus facile si le dénominateur est déjà une puissance de 10.
  4. Image intitulée Convert Fractions to Decimals Step 10
    4
    Multipliez votre fraction par une autre égale à 1. Cette dernière aura en dénominateur une valeur telle que le produit des deux dénominateurs donnera une puissance de 10. Cette seconde fraction aura un numérateur égal au dénominateur. C'est comme si vous aviez multiplié par 1.
    • En mathématiques, 1 est considéré comme un élément neutre pour la multiplication, c'est-à-dire que toute valeur multipliée par 1 la laisse inchangée. Donc, si vous multipliez une fraction quelconque par une fraction dont la valeur est 1, vous ne modifiez pas la fraction de départ, vous modifiez simplement sa présentation.
    • Ainsi, la fraction 2/2 est égale à 1 (2/2 = 1). Supposons que vous ayez à transformer la fraction 1/5 en une fraction avec en dénominateur de 10, vous devez la multiplier par 2/2. Vous obtenez alors : 2/10 (1/5 x 2/2 = 2/10 [3] ).
    • Pour faire le produit de deux fractions, on multiplie horizontalement. On multiplie les numérateurs entre eux et on fait de même avec les dénominateurs. Le résultat final est une nouvelle fraction avec ces deux résultats, aux mêmes places.
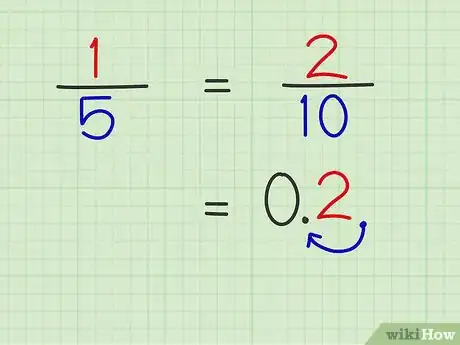
  5. Image intitulée Convert Fractions to Decimals Step 11
    5
    Convertissez ensuite votre fraction en puissance de 10 en nombre décimal. Prenez le numérateur et écrivez-le à part, en ajoutant une virgule à sa droite. Ensuite, vous comptez le nombre de zéros en dénominateur. Revenez à votre numérateur et déplacez votre virgule d'autant de rangs vers la gauche qu'il y a de zéros en dénominateur.
    • Si on reprend l'exemple de la fraction 2/10. Le dénominateur ne présente qu'un seul 0. On écrit à part le 2 du numérateur avec la virgule : « 2, » (la virgule ne change en rien la valeur) et comme il n'y a qu'un seul zéro, on déplace la virgule d'un rang vers la gauche : « 0,2 ».
    • Avec de la pratique, vous saurez vite convertir ces fractions un peu particulières. Dès que vous verrez une fraction avec en dénominateur une puissance de 10 ou une fraction avec en dénominateur un chiffre facilement transformable en puissance de 10, vous obtiendrez rapidement la valeur décimale correspondante.
    Publicité

Partie 4
Partie 4 sur 4:
Mémoriser certaines équivalences de fractions en nombres décimaux

  1. Image intitulée Convert Fractions to Decimals Step 12
    1
    Convertissez certaines fractions que vous voyez fréquemment passer. Nous vous le rappelons : il suffit, comme cela a été vu plus haut, de diviser le numérateur par le dénominateur (le nombre du haut par celui du bas).
    • Parmi ces fractions à connaitre, il y a : 1/4 (= 0,25), 1/2 (= 0,5) et 3/4 (= 0,75).
    • Si vous voulez avoir rapidement la valeur décimale d'une fraction, allez sur un moteur de recherche et tapez quelque chose comme « valeur décimale de 1/4 ». Vous pouvez aussi utiliser une calculatrice.
  2. Image intitulée Convert Fractions to Decimals Step 13
    2
    Vous pouvez aussi vous préparer de petites fiches cartonnées. À gauche, vous mettrez les fractions, et à droite, les valeurs décimales correspondantes. Au fil du temps, vous vous en servirez de moins en moins, car vous les connaitrez par cœur !
  3. Image intitulée Convert Fractions to Decimals Step 14
    3
    Avec de la pratique, toutes ces équivalences seront dans votre tête. Cela vous sera d'un très grand secours quand vous ferez des exercices de mathématiques plus complexes.
    Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
trouver X
Comment
trouver X
Publicité

Références

  1. ↑ http://www.mathsisfun.com/definitions/integer.html
  2. ↑ http://www.mathsisfun.com/definitions/dividend.html
  3. ↑ http://www.wyzant.com/resources/lessons/math/elementary_math/fractions/how_to_find_common_denominators

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 19 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 113 486 fois.
Catégories: Mathématiques
Résumé de l'articleX

Pour convertir une fraction en un nombre décimal, imaginez que la fraction est une division. Prenez le nombre du haut, le numérateur, et divisez-le par le nombre du bas, le dénominateur. Selon les cas, vous ferez le calcul de tête, à la main sur une feuille ou avec une calculatrice. Ainsi, pour transformer ¼ en nombre décimal, divisez 1 par 4, soit 0,25. Pour vérifier votre réponse, multipliez la réponse par le dénominateur : vous devriez retomber sur le numérateur !

Publicité