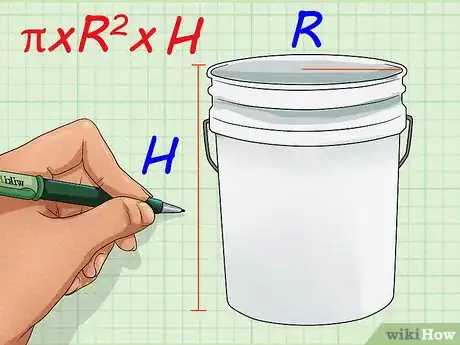Comment déterminer un volume en yards cubes

Informations concernant l'auteur.e

Le yard cube (en abrégé : « yd³ » ou « cu yd ») est une unité de mesure de volume qui correspond au volume contenu dans un cube qui ferait un yard de côté, soit environ 764,5 litres. Aux États-Unis, le yard cube est une unité de mesure largement utilisée dans différents domaines, par exemple, quand il s’agit d’estimer le volume de béton nécessaire pour un ouvrage. Si on prend l’exemple d’un volume parallélépipédique de longueur « L », de largeur « l » et de hauteur « H », le volume s’obtient en utilisant la formule suivante : Volume = L × l × H, étant entendu que L, l et H sont toutes exprimées en yards. Cet article utilise les abréviations américaines des unités de mesure (yd = yard).

Méthode 1

Méthode 1 sur 2:
Calculer le volume de figures en 3D

1
En premier, récupérez toutes les dimensions dont vous avez besoin, en yards. Pour toutes les figures classiques à trois dimensions, il existe des formules simples pour trouver leurs volumes. Dans notre cas, on part du principe que toutes les mesures seront en yards. En conséquence, avant d’utiliser une quelconque formule, il faudra vous assurer que toutes les mesures ont été faites en yards et si ce n’est pas le cas, il faudra faire une conversion. Voici quelques-unes de ces conversions :
- 1 yard = 3 pieds
- 1 yard = 36 pouces
- 1 yard = 0,914 mètre
- 1 yard = 91,44 centimètres
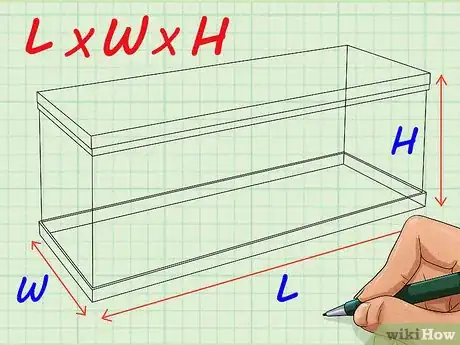
2
Pour des volumes parallélépipédiques, on utilise la formule suivante : L × l × H. Le volume d’une figure à trois dimensions et à faces rectangulaires (parallélépipède, cube, etc.) se calcule en multipliant sa longueur par sa largeur par sa hauteur. Cette formule peut être récrite en multipliant une des surfaces rectangulaires par la longueur de la face perpendiculaire.
- Par exemple, vous voulez calculer le volume de votre salle à manger (en yd³). Cette dernière fait 4 yd de long, 3 de large et 2,5 de haut. Pour calculer le volume de cette pièce, il suffit de multiplier la longueur par largeur et par la hauteur :
  - 4 × 3 × 2,5
  - = 12 × 2,5
  - = 30. La pièce a un volume de 30 yd³
- Un cube est un parallélépipède dont tous les côtés et tous les angles sont égaux. Partant, la formule de calcul du parallélépipède, L × l × H se transforme en : L x L x L, soit L³.
3
Pour des volumes cylindriques, on utilise la formule suivante : pi × R² × H. Pour calculer le volume d’un cylindre, il suffit de calculer la surface d’une des faces circulaires du cylindre, puis de multiplier par la hauteur du cylindre. La surface d’un cercle s’obtient en multipliant le carré du rayon par pi (3,1415926…), le rayon étant la distance entre le centre et n’importe quel point du cercle. Ensuite, il suffit de multiplier ce résultat par la hauteur du cylindre et vous avez le volume total de votre cylindre. Bien entendu, toutes les mesures doivent être exprimées en yards.
- Par exemple, vous voulez installer une fontaine derrière chez vous et vous avez besoin de creuser un trou cylindrique. Ce trou doit faire 1,5 yard de diamètre et 1 yard de profondeur. Première chose à faire : divisez le diamètre par 2 pour obtenir le rayon : 0,75 yard. Vous avez maintenant toutes vos données, vous pouvez calculer le volume du trou :
  - (3,14159) × 0,75² × 1
  - = (3,14159) × 0,5625 × 1
  - = 1,767. Votre trou aura un volume de 1,767 yd³
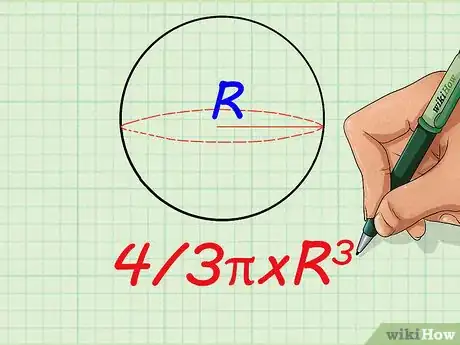
4
Pour des volumes sphériques, on utilise la formule suivante : 4/3 x pi × R³. Pour calculer le volume d’une sphère, tout ce dont vous avez besoin, c’est de connaitre le rayon, c’est-à-dire la distance du centre à n’importe quel point de la sphère, en yards. Élevez ce rayon au cube (multipliez le rayon trois fois par lui-même), puis multipliez par 4/3 et par « pi ». Avec cette formule, vous obtenez le volume de votre sphère en yards cubes.
- Par exemple, supposons que vous deviez calculer le volume d’air contenu dans une montgolfière. Cette dernière fait 10 yards de diamètre. Divisez 10 par deux pour obtenir le rayon de la montgolfière, soit 5 yards. Ensuite, faites l’application numérique dans la formule de calcul du volume de la sphère comme indiqué ci-dessous :
  - 4 /3 x pi × (5)³
  - = 4/3 (3,14159) × 125
  - = 4,189 × 125
  - = 523,6, Il y a 523,6 yd³ d’air dans la montgolfière
5
Pour des volumes coniques, on utilise la formule suivante : 1/3 x pi × R² × H. En fait, le volume d’un cône est égal à 1/3 du volume d’un cylindre qui aurait la même hauteur et le même rayon que le cône. Donc, pour un cône, il suffit de connaitre la hauteur et le rayon (en yards, bien sûr !) Avec ses deux mesures, faites comme si vous calculiez le volume d’un cylindre, puis multipliez votre résultat par 1/3.
- Par exemple, vous cherchez à calculer le volume d’un cornet de glace. Bien sûr, c’est un petit volume - disons qu’il a au sommet un rayon de 1 pouce sur une hauteur de 5. Converties en yards, ces mesures donnent respectivement 0,028 et 0,139 yard. Allons-y pour le calcul du volume :
  - 1/3 (3,14159) × 0,028² × 0,139
  - = 1/3 (3,14159) × 0,000784 × 0,139
  - = 1/3 × 0,000342
  - = 1,141^-4. Le cornet de glace a un volume de1,141^-4 yd³
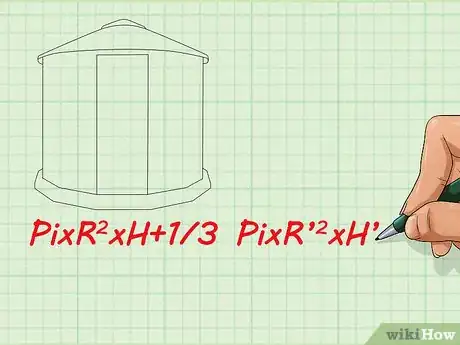
6
Pour les volumes de formes irrégulières, il faut procéder différemment. Si votre figure n’a pas de formule spécifique de calcul du volume, il faut diviser ce volume en volumes de base (en yards cubes) qu’on sait calculer. Au final, on additionnera tous ces petits volumes constitutifs du grand volume initial.
- Par exemple, vous devez calculer le volume d’un petit silo à grains. C’est un cylindre de 12 yards de haut et 1,5 yard de rayon. Ce silo est surmonté d’un toit conique de 1 yard de haut. Dans ce cas, vous calculez séparément le volume du toit, puis du silo et vous additionnez les deux. Donc, on obtient :
  - Pi ◊ R² × H (silo) + 1/3 Pi × R'² × H' (toit)
  - (3,14159) × 1,5² × 12 + 1/3 (3,14159) × 1,5² × 1
  - = (3,14159) × 2,25 × 12 + 1/3 (3,14159) × 2,25 × 1
  - = (3,14159) × 27 + 1/3 (3,14159) × 2,25
  - = 84,822 + 2,356
  - = 87,178. Le silo a un volume de 87,178 yards cubes
Publicité

Méthode 2

Méthode 2 sur 2:
Petite astuce pour calculer un volume de béton

1
Commencez par calculer la surface de votre ouvrage en béton. Admettons que vous ayez décidé de couler une terrasse derrière chez vous. Vous avez préparé un coffrage au sol qui a de quelques pouces à un pied de profondeur. Dans ce cas, il n’est pas nécessaire de recourir à des formules compliquées pour savoir la quantité de béton dont vous avez besoin ! Les entrepreneurs du BTP ont mis au point une méthode de calcul rapide pour connaitre le cubage d’un ouvrage parallélépipédique. Il faut d’abord connaitre la surface de l’ouvrage à couler.
- Attention ! dans ce cas, la surface doit être en pieds et non en yards, comme ci-dessus !
- Nous vous rappelons que pour les carrés ou les rectangles, la surface s’obtient en faisant longueur × largeur. Pour les cercles, la formule est : Pi ◊ R².
2
Ensuite, déterminez l’épaisseur de votre terrasse. C’est relativement simple - il vous suffit de mesurer la profondeur de votre coffrage. Pour simplifier les choses, la mesure doit être faite en pouces plutôt qu’en fraction de pied, car l’épaisseur est relativement faible.
3
Divisez votre surface par un coefficient qui est fonction de l’épaisseur du béton. Pour savoir la quantité de béton dont vous allez avoir besoin, il suffit de diviser votre surface par un certain nombre, lequel est inversement proportionnel à l’épaisseur. Plus votre terrasse sera fine, plus ce nombre sera élevé. À l’inverse, plus la terrasse sera épaisse, plus ce nombre sera faible. Voici quelques-uns de ces coefficients (si votre épaisseur n’est pas indiquée, passez à l’étape suivante).
- Si votre ouvrage fait 4 pouces d’épaisseur, divisez votre surface par 81 pour avoir votre volume en yards cubes.
- Si votre ouvrage fait 6 pouces d’épaisseur, divisez par 54.
- Si votre ouvrage fait 8 pouces d’épaisseur, divisez par 40.
- Si votre ouvrage fait 12 pouces (1 pied) d’épaisseur, divisez par 27.
4
Déterminez les coefficients par vous-même. Donc, vous n’avez pas trouvé votre épaisseur dans la partie précédente ! Voilà comment on procède : on divise 324 par l’épaisseur du projet (en pouces), ce sera votre coefficient. Ensuite, comme d’habitude, on multiplie la surface de section par ce coefficient. Vous avez votre cubage en yards cubes.
- Par exemple, vous avez un ouvrage d’une surface de 10 pieds × 10 pieds et d’une épaisseur de 3,5 pouces. Voici les calculs du volume de la dalle :
  - 324/3,5 = 92,6
  - 10 × 10 = 100
  - 100/92,6 = 1,08. Vous allez avoir besoin de 1,08 yd³ de béton
5
Commandez un peu plus que le volume calculé. En effet, il peut y avoir des erreurs de mesure. S’il vous reste du ciment, vous trouverez toujours à l’utiliser ailleurs. Si vous n’en avez pas assez, il va falloir interrompre votre travail pour aller en acheter. Or, le béton n’attend pas ! Il faut couler en une seule fois ! Donc, commandez plus, surtout si votre volume à couler est conséquent.

Publicité