wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 36 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 22 949 fois.
En algèbre, l'opération puissance est utilisée pour exprimer d'une manière plus simple la multiplication d'un nombre par lui-même plusieurs fois de suite. Au lieu d'écrire , vous pouvez simplement vous limiter à . Les puissances vous permettent d'écrire plus facilement des expressions ou des équations longues et complexes. En outre, vous pouvez faire des opérations d’addition et de soustraction avec les puissances pour simplifier des problèmes mathématiques selon le cas, et ce, une fois que vous les aurez maitrisées (par exemple : ).
Étapes
Partie 1
Partie 1 sur 3:Résoudre de simples opérations puissances
-
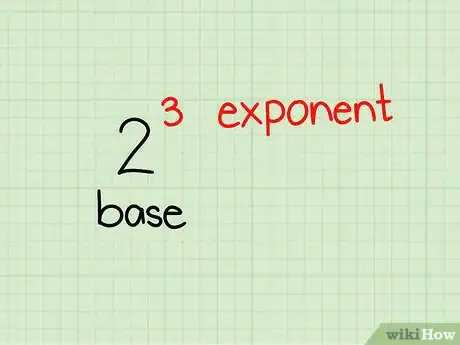
1Apprenez les terminologies des puissances. Les opérations puissances comme sont composées de deux parties toutes simples. Le nombre de facteurs intervenant dans cette opération mathématique, dans ce cas 2, est la base. Le petit nombre en haut, dans notre cas 3, est appelé l’exposant ou la puissance. se lit 2 puissance 3, 2 exposant 3 ou encore 2 élevé à la puissance 3.
- Si un nombre est élevé à la puissance 2, comme , on peut également dire que le nombre est au carré. Par exemple, cinq au carré.
- Si un nombre est élevé à la puissance 3, comme , on peut également dire que ce nombre est au cube. Par exemple, dix au cube.
- Si un nombre ne possède pas d'exposant, comme un simple 4, techniquement, il est élevé à la puissance 1 et peut être réécrit .
- Si l'exposant est 0, et que la base n’est pas égale à zéro, le résultat est toujours 1 comme , ou . Vous trouverez plus de détails à ce sujet dans la section Conseils.
-
2Multipliez la base par elle-même autant de fois que l'indique l'exposant. Si vous devez calculer une puissance à la main, commencez à la réécrire comme une opération de multiplication. Vous devez multiplier la base par elle-même autant de fois que l'indique l'exposant. Par exemple, si vous avez cette expression , vous devez multiplier le chiffre 3 à 4 reprises, soit . Voici d'autres exemples :
- Dix au cube [1]
-
3Résolvez une expression. Multipliez les deux premiers chiffres entre eux pour trouver le produit. Par exemple, vous pouvez réécrire comme suit . Ce calcul semble assez complexe, mais allez-y pas à pas. Commencez en multipliant les deux premiers 4. Par la suite, réécrivez l'expression en remplaçant les deux premiers 4 par leur produit, comme le montre l'exemple suivant :
-
-
4Multipliez le produit du premier calcul (16) avec le chiffre suivant. Continuez de cette façon pour faire « accroitre » votre exposant. Avec notre exemple, vous devez multiplier 16 par le prochain 4, si bien que :
-
-
-
- Comme indiqué, vous devez continuer à multiplier la base du produit de la première paire de nombres jusqu'à ce que vous obteniez le résultat final. Vous devrez procéder de la sorte en multipliant les deux premiers nombres entre eux, puis en multipliant la réponse obtenue par le chiffre suivant dans la séquence. Cette logique est valable, quel que soit l'exposant. À la fin des calculs, vous aurez .
-
-
5Utilisez une calculatrice pour vérifier vos réponses.
-
6Tapez les touches "exp," "" ou "^" sur une calculatrice. Il est quasiment impossible de faire des opérations à la main avec de très grands exposants, comme . Mais avec les calculatrices, vous aurez une facilité à le faire. La touche à utiliser est clairement indiquée en général. La calculatrice de Windows 7 peut être utilisée comme une calculatrice scientifique en tapant sur la touche "View" et en sélectionnant l'option "Scientific". Lorsque vous souhaitez restaurer la version standard, tapez sur le bouton "View" et puis sélectionnez "Standard".
- Tapez votre expression mathématique dans Google pour vérifier votre réponse. Pour ce faire, vous pouvez utiliser la touche "^" sur le clavier de votre ordinateur, votre tablette ou votre smartphone. Vous obtiendrez immédiatement la réponse ainsi que d’autres expressions similaires.
Publicité
Partie 2
Partie 2 sur 3:Additionner, soustraire et multiplier des exposants
-
1Additionnez et soustrayez les termes ayant la même base et le même exposant. Dans de tels cas, par exemple , vous pouvez simplifier votre expression mathématique en une opération de multiplication. Rappelez-vous que peut être considéré comme , ce qui veut dire que . Il vous suffit d’additionner les nombres des termes similaires (ayant la même base et le même exposant) et de multiplier la somme par l’exposant. À ce stade, vous n’aurez qu’à résoudre le et multiplier la solution par deux. N’oubliez pas que ceci tient au fait que la multiplication est une façon de réécrire une addition, étant donné que . Voici quelques exemples [2] :
-
2Multipliez les termes ayant la même base en additionnant les exposants. Si vous avez deux termes avec la même base tels que , tout ce que vous devez faire, c’est d’additionner les exposants. Donc : . Si vous êtes un peu confus, décomposez l’expression :
- Puisque le même nombre est multiplié par lui-même dans toute l’expression, on peut dire que :
- [3] .
-
3Multipliez un nombre exponentiel élevé à une autre puissance. Prenons cet exemple . Si vous avez un nombre élevé à une puissance donnée et que cet ensemble est élevé à un autre exposant, il vous suffit de multiplier les exposants entre eux. Donc : . Une fois encore, si vous avez des doutes, pensez à ce que ces symboles signifient vraiment. signifie en d’autres termes que vous devez multiplier à 5 reprises le terme suivant.
- Étant donné que la base est constante, on peut procéder simplement à une sommation des exposants : .
-
4Considérez les exposants négatifs comme des fractions ou l’inverse du nombre. Si vous n’y comprenez pas grand-chose, ne vous inquiétez pas. Lorsque vous avez un terme avec un exposant négatif, par exemple , replacez le terme en question avec l’opposé de son exposant sous une fraction dont le numérateur est égal à 1, comme . Voici d’autres exemples.
-
5Divisez deux termes ayant la même base en soustrayant les exposants. La division est l'opération inverse de la multiplication et, bien qu'il ne soit toujours pas possible de les résoudre de façon exactement inverse, c’est le cas ici. Si vous devez résoudre l'opération , il vous suffit de soustraire l'exposant du dénominateur de celui du numérateur, en gardant la base. Par conséquent, , ou 16.
- Nous verrons plus loin que toute puissance qui fait partie d'une fraction, par exemple , peut être réécrite sous la forme . Les exposants négatifs entrainent des fractions.
-
6Habituez-vous à résoudre les opérations avec des exposants. Les expressions suivantes portent sur tout ce qui vient d’être expliqué.
- =
- =
- =
- = N’oubliez pas : un nombre sans exposant est toujours à la puissance 1.
- =
- =
Publicité
Partie 3
Partie 3 sur 3:Résoudre des exposants fractionnaires
-
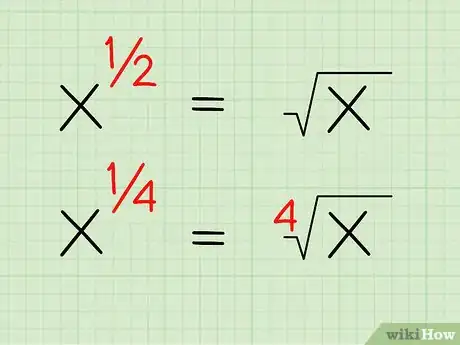
1Considérez les exposants fractionnaires () comme la racine d'un nombre. L'expression mathématique est exactement identique à celle-ci . Cela est possible, quel que soit le dénominateur de la fraction, donc serait la racine quatrième de X, que l'on peut également écrire sous cette forme .
- Les racines sont l’inverse des exposants. Si l'on considère la réponse de cette opération et que nous l'élevons à la puissance 4, nous obtiendrons . Par exemple peut être réécrit comme suit. De même, si , alors , et par conséquent .
-
2Écrivez le numérateur sous la forme d’un exposant dans le cas des fractions mixtes. L’expression pourrait sembler très complexe, mais vous pouvez facilement la résoudre si vous vous souvenez des calculs de multiplications des exposants. Transformez la base en une racine, comme une fraction normale, puis élevez le tout à la puissance indiquée par le numérateur. Si vous avez du mal à vous en souvenir, examinez en détail ce théorème. Après tout, égal à . Voici un exemple.
- =
-
3Additionnez, soustrayez et multipliez les puissances fractionnaires normalement. Il est généralement beaucoup plus facile d’additionner et de soustraire les puissances fractionnaires avant de les résoudre ou de les réécrire sous forme d'un radical. Si les puissances sont identiques et que les bases le sont également, vous pouvez procéder normalement à la somme et la soustraction des termes. Si les bases sont identiques, vous pouvez également multiplier et diviser les puissances normalement. Si vous avez oublié comment additionner et soustraire des fractions, consultez cet article. Voici un exemple :Publicité
Conseils
- La plupart des calculatrices possèdent une touche pour simplifier les calculs des puissances. Vous aurez à taper l’exposant comme un nombre positif ou négatif après avoir tapé le nombre représentant la base. Cette touche est généralement sous le symbole ^ ou x ^ y.
- « Simplifier » en mathématiques revient à suivre une opération en particulier pour obtenir la forme la plus simple d’une expression.
- Le chiffre 1 est l'élément neutre de l’exponentiation. Cela signifie que tout nombre élevé à la puissance 1 est égal au nombre lui-même, par exemple . En outre, 1 est l'élément neutre de la multiplication (lorsque 1 est utilisé comme un multiplicateur, le résultat ne change pas, comme ), et 1 est l’élément neutre de la division (lorsque 1 est utilisé comme un diviseur, comme .)
- Le chiffre zéro à la puissance zéro, c’est-à-dire 00, n’est pas défini. Les ordinateurs et les calculatrices vous donneront comme résultat « erreur ». Rappelez-vous que tout nombre réel autre que 0 à la puissance zéro est toujours égal à 1, par exemple
- En algèbre avancée pour les nombres imaginaires , où , e est une constante irrationnelle approximativement égale à 2,71828... et a est une constante arbitraire. La preuve de cette relation peut être trouvée dans la plupart des livres de mathématiques de niveau supérieur.
Avertissements
- En augmentant la valeur des exposants, vous pourriez très rapidement obtenir des résultats astronomiques, de sorte que même si vous croyez que vos réponses semblent être fausses, elles pourraient être correctes. Vous pouvez vérifier cela vous-même en représentant le graphique d'une fonction exponentielle. Par exemple, 2x, où x présente un intervalle de valeurs.
Références
- ↑ http://www.rapidtables.com/math/number/exponent/adding-exponents.htm#same-base
- ↑ http://www.purplemath.com/modules/exponent.htm
- ↑ http://www.rapidtables.com/math/number/exponent/adding-exponents.htm#same-base
- ↑ http://www.rapidtables.com/math/number/exponent/adding-exponents.htm#same-base
- ↑ http://www.purplemath.com/modules/exponent.htm









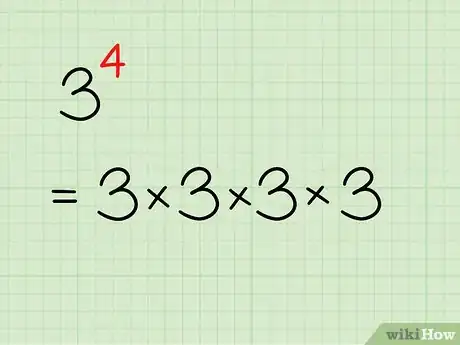








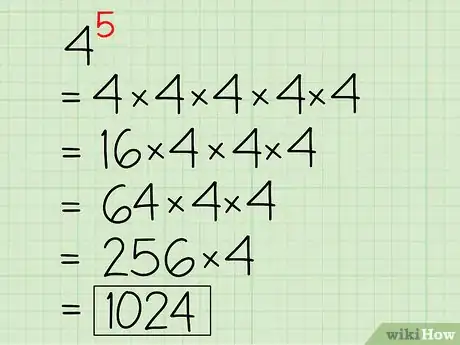











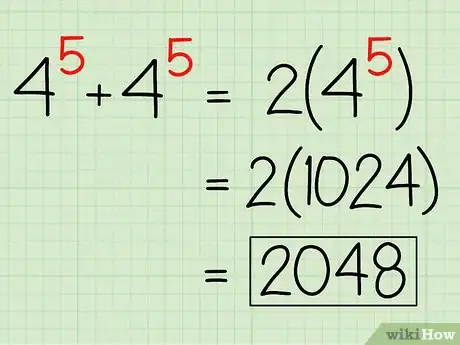















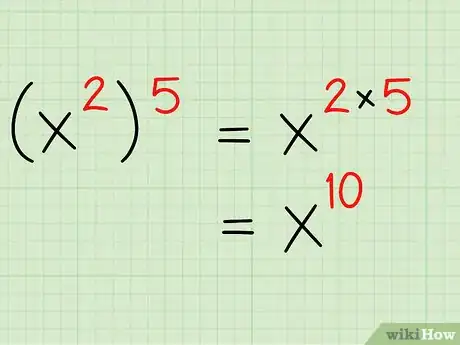





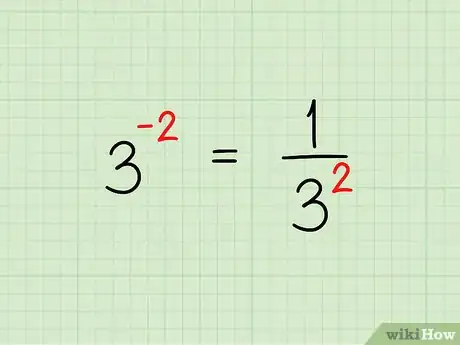



















![{\sqrt[ {4}]{x}}](./images/1463099168-6193130540098748b8aecf0b95bf490c2ae3d867.webp)

![{\sqrt[ {4}]{16}}=2](./images/1547247300-5dc7611c792190a491115fad8596026987d51cb7.webp)

![{\sqrt[ {4}]{x}}=2](./images/2233409683-e178eca22cc5d6a49d2fbda5c6c18a1ec1669fb2.webp)







![x^{{{\frac {1}{3}}}}={\sqrt[ {3}]{x}}](./images/2160271401-759eade6ce89e27b301ccdcd83d7e8858827b8e2.webp)
![({\sqrt[ {3}]{x}})^{5}](./images/1642208928-8ea002d6365c3ba2d1d255162136605453a7135f.webp)



























