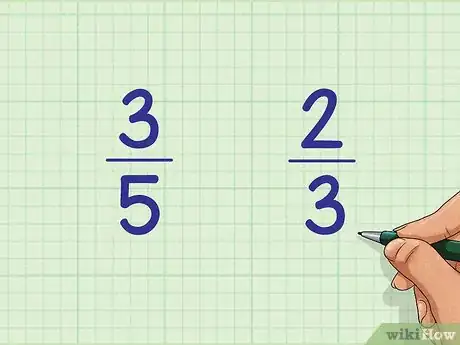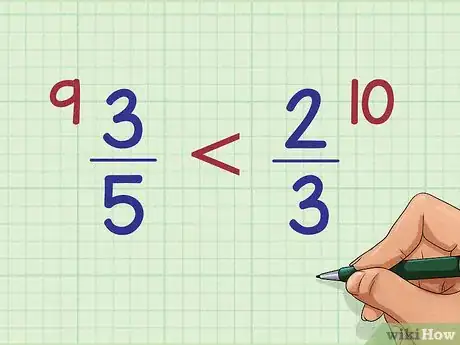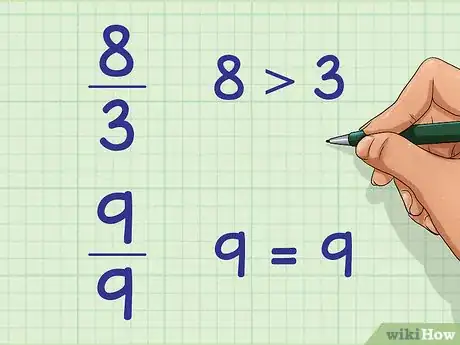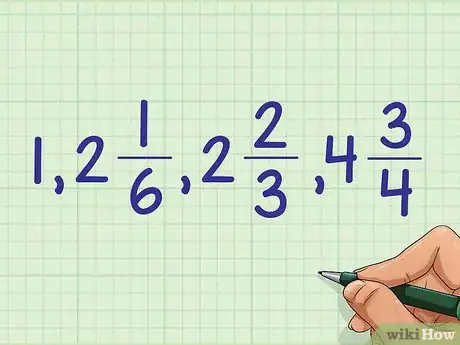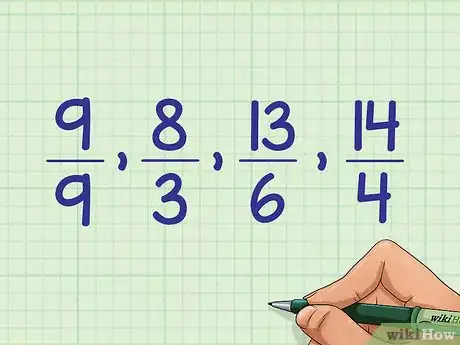Comment ordonner des fractions de la plus petite à la plus grande

Coécrit par David Jia

S'il est facile de classer des entiers (ou même des nombres décimaux) par ordre croissant, la tâche devient beaucoup moins évidente quand il s'agit d'ordonner des fractions. Si tous vos dénominateurs (valeurs sous la barre de fraction) sont identiques, alors il faut classer les fractions par ordre de numérateur croissant. Ainsi, 1/5, 3/5 et 8/5 sont classés par ordre croissant. Sinon, il va falloir modifier vos fractions pour qu'elles aient le même dénominateur, afin de retomber dans le cas précédent. Cette réduction au même dénominateur est assez simple, à condition de connaitre les bonnes méthodes. Nous allons vous indiquer ici comment on fait, même avec des fractions « impropres » comme 7/3.

Méthode 1

Méthode 1 sur 3:
Comparer deux ou plusieurs fractions

1
Trouvez le plus petit commun dénominateur à toutes les fractions. Pour cela, il existe plusieurs méthodes que nous allons voir. Le principe de base est simple, il faut transformer les fractions de façon à ce qu'elles aient le même dénominateur. Cette opération mathématique s'appelle la réduction au même dénominateur, lequel est le plus petit commun multiple des dénominateurs. Quelques explications ^{[1]
X
Source de recherche}.
- Multipliez entre eux tous les dénominateurs distincts. Par exemple, vous devez comparer 2/3, 5/6 et 1/3. Multipliez les deux seuls dénominateurs distincts : 3 x 6 = 18. Ici, on obtient un nombre assez simple, mais parfois, on obtient des nombres plus élevés (ex. : 286), plus difficiles à manipuler par la suite.
- Sinon, dressez la liste des multiples de chacun des dénominateurs jusqu'à en trouver un présent dans toutes les listes. Prenez le plus petit. Par exemple, vous devez toujours comparer 2/3, 5/6 et 1/3. Dressez la liste des multiples de 3 (3, 6, 9, 12, 15, 18…), puis celle des multiples de 6 (6, 12, 18…). Vous avez un multiple commun, prenez le plus petit s'il y en a plusieurs. Ici, c'est 18. C'est votre PPCM (plus petit commun multiple).
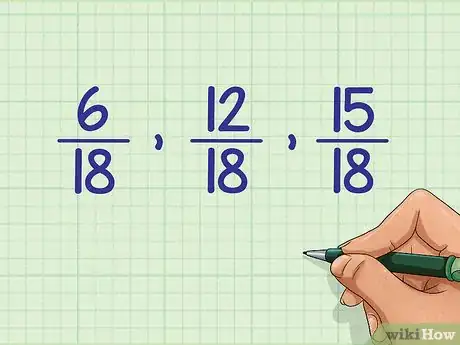
2
Transformez chacune des fractions de façon à ce qu'elles aient le même dénominateur. Nous vous rappelons que quand on multiplie un dénominateur par une valeur, il faut faire de même avec le numérateur pour que la fraction reste inchangée. Il faut réduire toutes vos fractions au même dénominateur. On a donc nos trois fractions : 2/3, 5/6 et 1/3. Le dénominateur commun est 18, il faut ramener toutes les fractions sur 18 :
- 18 ÷ 3 = 6 –il faut multiplier la première fraction par 6/6, ce qui donne : 2/3 x 6/6 = (2x6)/(3x6) = 12/18
- 18 ÷ 6 = 3 –il faut multiplier la deuxième fraction par 3/3, ce qui donne : 5/6 x 3/3 = (5x3)/(6x3) = 15/18
- 18 ÷ 3 = 6 –il faut multiplier la troisième fraction par 6/6, ce qui donne : 1/3 x 6/6 = (1x6)/(3x6) = 6/18
3
Ensuite, il suffit de comparer les numérateurs pour effectuer le classement. Comme les trois fractions ont le même dénominateur, c'est un jeu d'enfant de les classer. Comparez les numérateurs (valeurs au-dessus du trait de fraction) : celle qui a le plus petit numérateur est la plus petite fraction, etc. Ainsi, le classement est le suivant : 6/18, 12/18, 15/18.
4
Enfin, il faut redonner aux fractions, maintenant qu'on les a classées, leurs formes originelles. Ne changez pas leur ordre ! Redonnez-leur leur forme de départ. Soit vous regardez les calculs que vous avez faits précédemment, soit vous refaites les calculs en sens inverse. Vous divisez alors le numérateur et le dénominateur par la valeur que vous avez précédemment utilisée, ce qui donne :
- 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
- 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
- 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
- Le classement par ordre croissant est le suivant : 1/3, 2/3, 5/6
Publicité

Méthode 2

Méthode 2 sur 3:
Classer deux fractions en utilisant le produit en croix

1
Inscrivez vos deux fractions assez proches l'une de l'autre. Admettons que l'on veuille comparer 3/5 et 2/3. Laquelle est la plus grande ? Mettez par exemple 3/5 à gauche et 2/3 à droite.
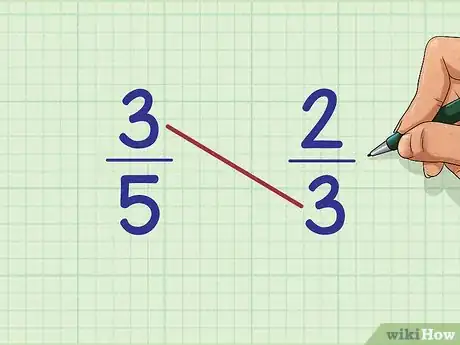
2
Multipliez le numérateur (valeur du haut) de la première fraction par le dénominateur (valeur du bas) de la seconde fraction. Dans notre exemple, le numérateur de la première fraction (3/5) est 3. Le dénominateur de la seconde fraction (2/3) est aussi 3. Multipliez-les et inscrivez : 3 x 3 = ?
- Cette méthode s'appelle le produit en croix, parce qu'on a multiplié en diagonale.
3
Inscrivez ce résultat en haut à gauche de la première fraction. Mettez-le sous la forme d'un petit chiffre. Dans notre exemple, on a : 3 x 3 = 9. Ce 9, vous allez le noter à la place que nous vous avons donnée.
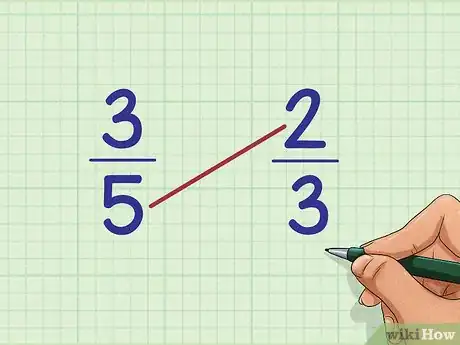
4
Multipliez le numérateur (valeur du haut) de la seconde fraction par le dénominateur (valeur du bas) de la première fraction. Pour pouvoir comparer, deux fractions, il faut faire la seconde partie du produit en croix. Multipliez ces deux valeurs. Ainsi, avec 3/5 et 2/3, il faut multiplier 2 et 5 (résultat : 10).
5
Comme précédemment, inscrivez le résultat en haut, mais à droite cette fois. Avec notre exemple, mettez un petit 10.
6
Il ne reste plus qu'à comparer ces deux produits. La fraction qui porte la valeur (issue du produit en croix) la plus grande est la fraction la plus grande. Ici, on a 9 et 10 comme valeurs du produit en croix, donc la fraction qui porte le 10 est supérieure à la fraction qui porte le 9. Traduit en fractions, 2/3 est supérieur à 3/5.
- Rappel : on inscrit le produit du côté du numérateur utilisé.
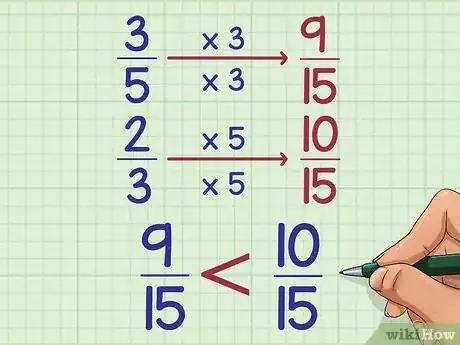
7
Regardons de plus près le principe de calcul. On l'a dit plus haut, pour comparer deux fractions, il faut les ramener au même dénominateur. À bien y regarder, c'est qu'on fait en faisant le produit en croix ^{[2]
X
Source de recherche} ! On rejoint ici la méthode qui consiste à multiplier les dénominateurs sans chercher à trouver le plus petit commun dénominateur. Prenons notre exemple pour être plus clair. 15 serait le produit des dénominateurs (3 x 5). Donc, il faut multiplier le premier numérateur par 3 et le second par 5. C'est exactement ce qu'on a fait avec le produit en croix. Donc, comme les dénominateurs sont identiques, on ne compare que les numérateurs. Voici le détail :
- 3/5 = (3x3)/(5x3) = 9/15
- 2/3 = (2x5)/(3x5) = 10/15
- 9/15 est plus petit que 10/15
- Donc, 3/5 est plus petit que 2/3
Publicité

Méthode 3

Méthode 3 sur 3:
Classer des fractions impropres (> 1)

1
La méthode qu'on va vous exposer ne concerne que les fractions dont le numérateur est supérieur ou égal au dénominateur. C'est ce qu'on appelle une fraction impropre. Exemple : 8/3 est une fraction impropre, car 8 > 3. De même, 9/9 en est une, même si elle est un peu particulière ^{[3]
X
Source de recherche}.
- Ces fractions peuvent être classées selon les méthodes décrites plus haut. Cependant, celle que nous allons vous présenter est plus logique, et certainement plus rapide.
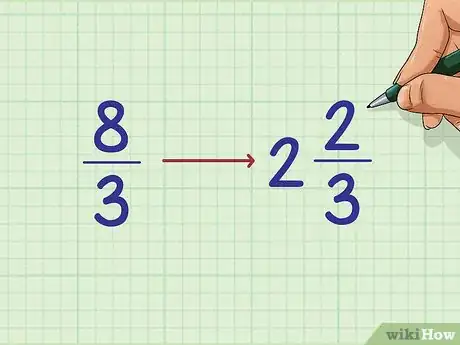
2
Convertissez chacune des fractions en nombres fractionnaires (ou mixtes). Ces derniers se composent d'un nombre (ou d'un chiffre) entier suivi d'une fraction. Parfois, on peut le faire de tête si la fraction n'est pas trop compliquée. Par exemple, 9/9 = 1. D'autres fois, il faudra poser la division pour trouver combien de fois le dénominateur va dans le numérateur. Le résultat sera votre entier. Si votre division a un reste, ce dernier sera le numérateur de la partie fractionnaire de votre nombre mixte. Prenons un exemple concret avec 4 fractions qu'on veut classer :
- 8/3 = 2 + 2/3 (8 divisé par 3 donne 2 et il reste 2)
- 9/9 = 1
- 19/4 = 4 + 3/4 (19 divisé par 4 donne 4 et il reste 3)
- 13/6 = 2 + 1/6 (13 divisé par 6 donne 2 et il reste 1)
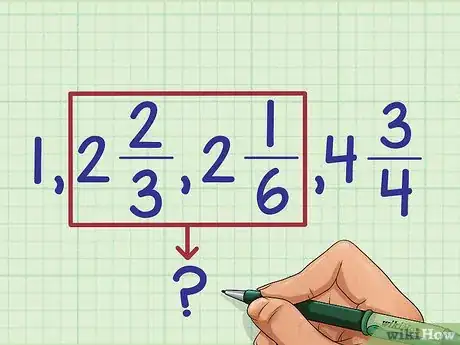
3
En ne prenant en compte que la partie entière, classez les nombres fractionnaires comme si vous aviez à classer à des nombres entiers. Pour l'instant, ne cherchez pas à classer les nombres qui ont la même partie entière. Voici ce que cela donne avec nos 4 fractions :
- 1 est le plus petit nombre fractionnaire
- 2 + 2/3 et 2 + 1/6 (des deux, on ne sait pas lequel est le plus grand)
- 4 + 3/4 est le plus grand.
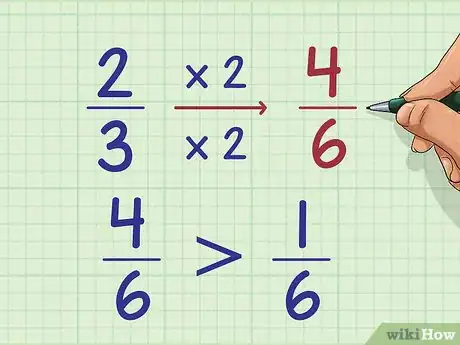
4
En cas de nombres fractionnaires ayant la même partie entière, il faudra appliquer l'une des méthodes vues précédemment. On va prendre la méthode de la réduction au même dénominateur pour départager 2 + 2/3 et 2 + 1/6. Voici ce que cela donne avec un dénominateur commun, 6 :
- 2/3 = (2x2)/(3x2) = 4/6
- 1/6 = 1/6
- 4/6 est plus grand que 1/6
- 2 + 4/6 est plus grand que 2 + 1/6
- 2 + 2/3 est donc plus grand que 2 + 1/6
5
Vous pouvez à présent finaliser votre classement. Par ordre croissant, les fractions se classent ainsi : 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
6
Reconvertissez les nombres mixtes en fractions impropres. Souvenez-vous, nous étions parties de fractions impropres ! Il faut donc, pour respecter les données de votre exercice, remettre les fractions originelles. Ainsi, de la plus petite à la plus grande, on a : 9/9, 8/3, 13/6 et 19/4. CQFD !

Publicité

Conseils

Si vous avez à classer un grand nombre de fractions, il est peut-être judicieux de grouper les fractions en petits sous-groupes (de 2, 3 ou 4 fractions), puis de classer par ordre croissant à l'intérieur de ces groupes et enfin, de réunir le tout.
Il est toujours plus facile de travailler avec le PPCM, mais rien ne vous empêche de prendre un autre multiple plus grand. Ainsi, avec 2/3, 5/6 et 1/3, vous pouvez très bien prendre comme dénominateur commun, 36. Vous devriez obtenir le même résultat.
Cas particulier : admettons que vous deviez classer par ordre croissant des fractions ayant toutes en numérateur le chiffre 1, comme 1/8 - 1/7 - 1/6 - 1/5. Le classement se ferait par ordre de dénominateur décroissant. On aurait ainsi : 1/8 < 1/7 < 1/6 < 1/5. Pour bien comprendre, pensez à une pizza qu'on découperait entre 5, 6, 7 ou 8 personnes (dont vous !). Devinez dans quel cas vous auriez la part la plus petite (ou la plus grosse) ? Facile, non ?