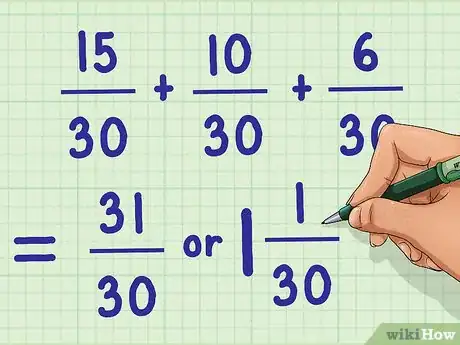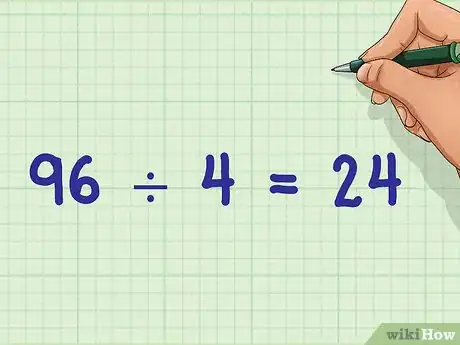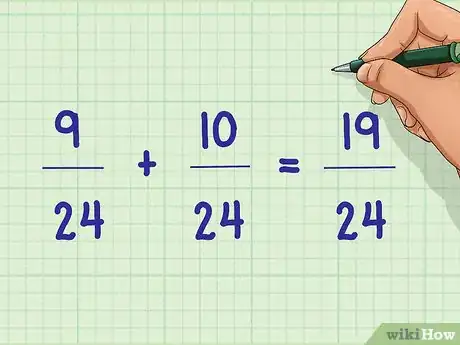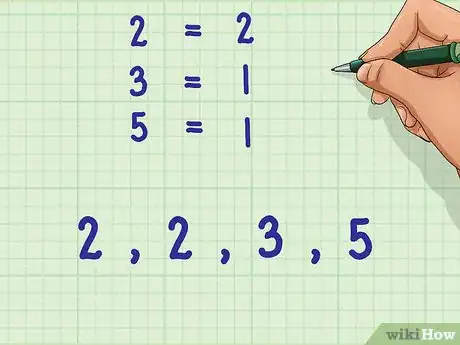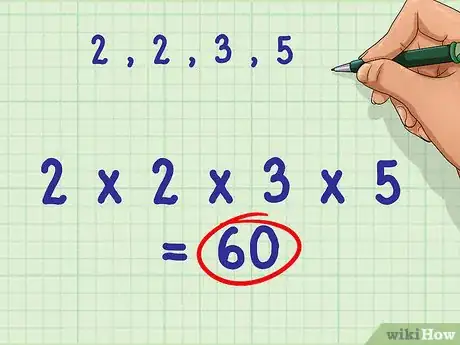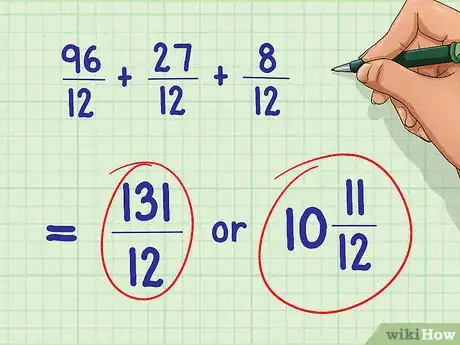X
Cet article a été coécrit par Mario Banuelos, PhD. Mario Banuelos est professeur adjoint de mathématiques à l'université d'État de Californie, à Fresno. Il a plus de huit ans d'expérience dans l'enseignement, et il est spécialisé dans la biologie mathématique, l'optimisation, les modèles statistiques pour l'évolution du génome et la science des données. Mario est titulaire d'une licence en mathématiques de l'université d'État de Californie, Fresno, et d'un doctorat en mathématiques appliquées de l'université de Californie, Merced. Mario a enseigné à la fois au lycée et à l'université.
Il y a 7 références citées dans cet article, elles se trouvent au bas de la page.
Cet article a été consulté 120 649 fois.
Pour effectuer des opérations d’addition et de soustraction arithmétiques sur des nombres fractionnaires ayant des dénominateurs différents, vous devrez en premier lieu rechercher leur plus petit dénominateur commun. Il s’agit du multiple le plus petit commun à chaque dénominateur de l’équation, soit du nombre entier le plus petit qui puisse être divisé par chacun des dénominateurs d’une équation[1] . On le connait également sous le terme arithmétique de PPCM. Bien que cette terminologie fasse référence à des nombres entiers, les algorithmes de calcul du plus petit dénominateur commun et du plus petit multiple commun sont similaires. Lorsque vous aurez déterminé le dénominateur commun, vous pourrez procéder simplement à l’addition ou à la soustraction des nombres fractionnaires de vos équations.
Étapes
Méthode 1
Méthode 1 sur 4:Établir une liste de multiples des dénominateurs[2]
Méthode 1
-
1Listez les multiples de chaque dénominateur. Établissez des listes de plusieurs multiples de chacun des dénominateurs de votre équation en les multipliant par des nombres entiers, par exemple 1, 2, 3, 4 et ainsi de suite.
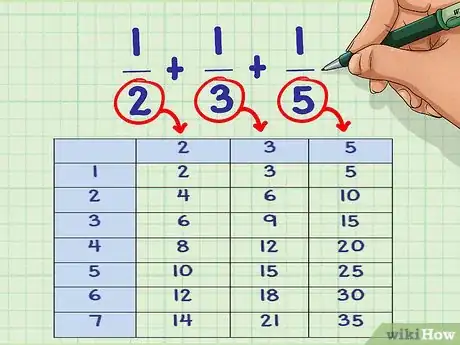
- Exemple: 1/2 + 1/3 + 1/5.
- Multiples de 2 : 2 * 1 = 2 ; 2 * 2 = 4 ; 2 * 3 = 6 ; 2 * 4 = 8 ; 2 * 5 = 10 ; 2 * 6 = 12 ; 2 * 7 = 14 ; etc.
- Multiples de 3 : 3 * 1 = 3 ; 3 * 2 = 6 ; 3 *3 = 9 ; 3 * 4 = 12 ; 3 * 5 = 15 ; 3 * 6 = 18 ; 3 * 7 = 21 ; etc.
- Multiples de 5 : 5 * 1 = 5 ; 5 * 2 = 10 ; 5 * 3 = 15 ; 5 * 4 = 20 ; 5 * 5 = 25 ; 5 * 6 = 30 ; 5 * 7 = 35 ; etc.
-
2Repérez les multiples communs les plus petits. Révisez chacune de vos listes et repérez tous les multiples communs à tous les dénominateurs provenant de l’équation, puis choisissez le plus petit d’entre eux.
- Si, arrivé à ce point, vous n’avez pas encore trouvé de dénominateur qui soit commun à toutes vos fractions, vous devrez continuer votre liste avec des multiples plus élevés, jusqu’à ce que vous en trouviez un qui le soit.
- Cette méthode est la plus appropriée si les dénominateurs de vos fractions sont petits.
- Dans cet exemple, le dénominateur commun à toutes les fractions est 30 : 2 * 15 = 30 ; 3 * 10 = 30 ; 5 * 6 = 30.
- Le dénominateur commun le plus petit (PPCD) sera donc 30
-
3Reposez votre équation originale sur le papier. Pour modifier tous les termes de votre équation afin que chacun d’entre eux conserve une même proportionnalité par rapport aux autres termes, vous devrez multiplier chaque numérateur et chaque dénominateur par le même facteur qui vous a servi à établir le dénominateur commun le plus petit.
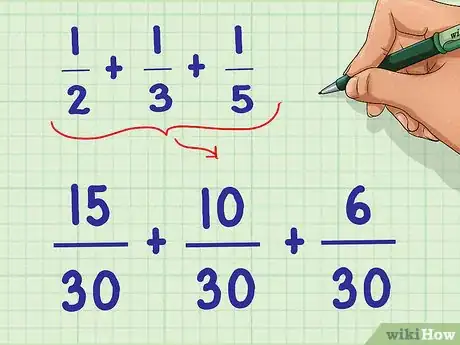
- Dans cet exemple: (15/15) * (1/2) ; (10/10) * (1/3) ; (6/6) * (1/5).
- La nouvelle équation sera donc: 15/30 + 10/30 + 6/30.
-
4Établissez maintenant la solution du problème. Lorsque vous aurez trouvé le dénominateur commun le plus petit et modifié vos fractions en conséquence, vous devriez être en mesure de résoudre votre problème sans aucune difficulté. Lorsque vous y serez arrivé, n’oubliez pas de simplifier si possible votre résultat.
- Dans notre exemple : 15/30 + 10/30 + 6/30 = 31/30 soit 1 1/30.
Publicité
Méthode 2
Méthode 2 sur 4:Utiliser le plus grand diviseur commun[3]
Méthode 2
-
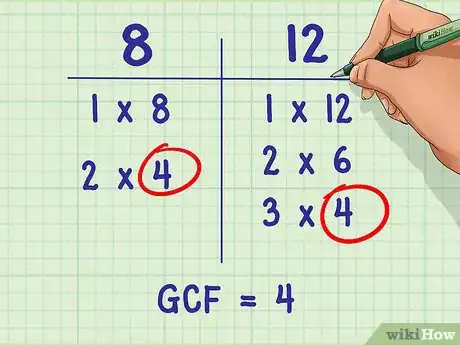
1Établissez la liste des facteurs de chaque dénominateur. Les facteurs d’une valeur entière sont une liste de nombres entiers par lesquels elle est divisible sans reste[4] . Le nombre 6 a par exemple 4 facteurs : 6, 3, 2 et 1. Tous les nombres ont en commun le facteur 1 parce que tous sont divisibles par 1.
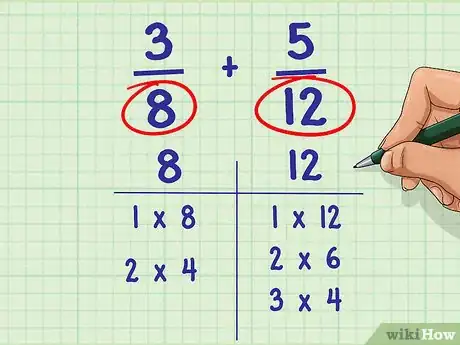
- Par exemple : 3/8 + 5/12.
- Les facteurs de 8 sont : 1, 2, 4, et 8.
- Les facteurs de 12 sont : 1, 2, 3, 4, 6, 12.
-
2Repérez le facteur le plus grand commun aux deux dénominateurs. Une fois que vous aurez établi la liste des facteurs composant chaque dénominateur, faites un repère sur tous ceux qu’ils ont en commun. C’est le plus grand de ces facteurs communs qui devra être utilisé dans la résolution de votre équation.
- Dans notre exemple, 8 et 12 ont en commun les facteurs 1, 2, et 4.
- Le plus grand de ces facteurs communs est 4.
-
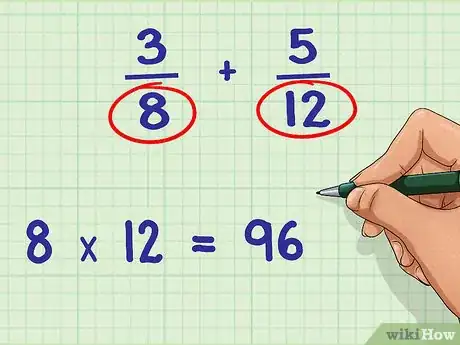
3Multipliez les dénominateurs ensemble. Pour pouvoir utiliser le plus grand diviseur commun dans la résolution de votre problème ,vous devez d’abord multiplier les deux dénominateurs ensemble.
- Dans notre exemple, vous obtiendrez : 8 * 12 soit 96.
-
4Divisez ensuite ce résultat par le plus grand facteur commun. Lorsque vous aurez obtenu le produit des deux dénominateurs, divisez-le par le plus grand facteur commun que vous avez obtenu précédemment. Le résultat de cette opération sera le plus petit dénominateur commun.
- Dans notre exemple, vous obtiendrez : 96 / 4 soit 24.
-
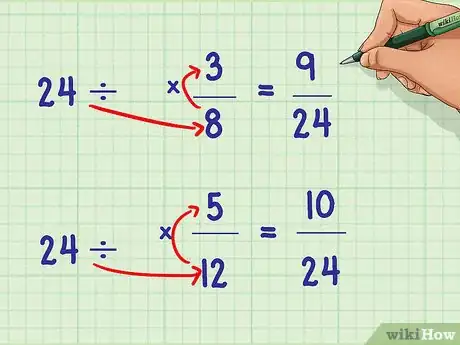
5Divisez le plus petit diviseur commun par le dénominateur initial. Afin de conserver la même proportionnalité entre les fractions de votre équation, il vous faut calculer pour chacune des fractions le nombre par lequel vous devrez en multiplier le numérateur et le dénominateur. Les dénominateurs des fractions seront maintenant égaux au dénominateur commun le plus petit.
- Dans notre exemple : 24 / 8 = 3 et 24 / 12 = 2.
- (3/3) * (3/8) = 9/24 et (2/2) * (5/12) = 10/24.
- 9/24 + 10/24.
-
6Passez maintenant à la résolution du problème. Lorsque vous aurez trouvé le dénominateur commun le plus petit, vous devriez être en mesure d’apporter facilement une solution à votre problème sans aucune difficulté. N’oubliez pas de simplifier si possible le résultat que vous obtiendrez.
- Dans notre exemple : 9/24 + 10/24 soit 19/24.
Publicité
Méthode 3
Méthode 3 sur 4:Décomposer chaque dénominateur en produit de facteurs premiers[5]
Méthode 3
-
1Décomposez chaque dénominateur en produit de facteurs premiers. Chaque dénominateur doit être décomposé en une suite de nombres premiers qui se multiplient entre eux pour le former. Les nombres premiers sont la particularité de ne pas être divisibles (excepté par eux même ou par 1) [6] .
- Dans cet exemple : 1/4 + 1/5 + 1/12.
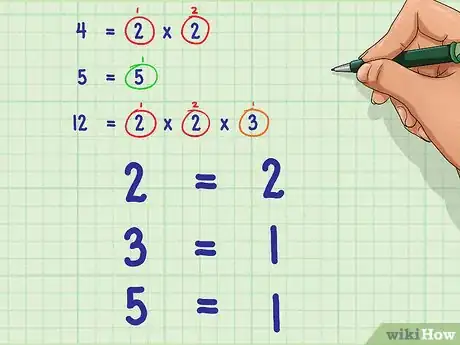
- Décomposition en nombre premiers de 4 : 2 * 2.
- Décomposition en nombre premiers de 5 : 5.
- Décomposition en nombre premiers de 12 : 2 * 2 * 3.
-
2Comptez le nombre de fois qu’un même facteur premier apparait lors de la réduction. Exprimez ensuite ce nombre premier en l’affectant du résultat de ce comptage en exposant.
- Par exemple : Il y a deux facteurs 2 dans les nombres 4 et 12, mais pas dans 5.
- Il y a un facteur 3 dans 12, mais pas dans les nombres 4 et 5.
- Il y a un facteur 5 dans 5, mais pas dans les nombres 4 et 12.
-
3Notez le plus grand nombre d’apparitions de chaque facteur premier. Lors de la décomposition de chacun des dénominateurs, comptez combien de fois apparait chaque facteur premier et mémorisez le plus grand nombre.
- Dans notre exemple : le chiffre 2 apparait deux fois et les chiffres 3 et 5 ne se présentent qu’une fois.
-
4Énumérez le facteur premier autant de fois que vous l’aurez compté dans l’étape précédente. Ne tenez pas compte du nombre de fois qu’il apparait pour l’ensemble des dénominateurs initiaux, mais seulement de la manière définie lors de l’étape précédente.
- Par exemple : 2, 2, 3, 5.
-
5Multipliez tous les nombres premiers énumérés de cette façon. Multipliez tous les facteurs premiers entre eux comme ils apparaissaient dans l’étape précédente. Le produit de cette multiplication vous donnera le plus petit dénominateur commun de l’équation initiale.
- Dans notre exemple: 2 * 2 * 3 * 5 = 60.
- Le plus petit dénominateur commun sera 60.
-
6Divisez maintenant le plus petit dénominateur commun par le dénominateur initial. Pour pouvoir déterminer le multiple dont vous aurez besoin pour maintenir la proportionnalité de chaque terme de votre équation, vous devrez diviser le PPCD que vous avez calculé par le dénominateur initial. Multipliez ensuite le numérateur et le dénominateur de chacune de vos fractions par ce nombre. Les deux dénominateurs doivent maintenant être égaux au plus petit dénominateur commun.
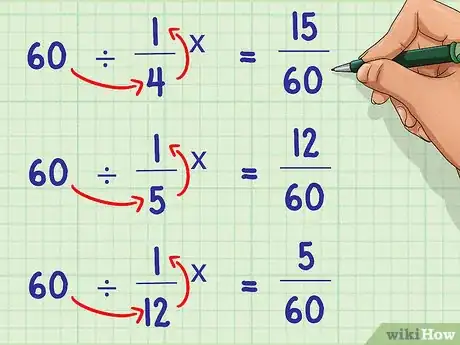
- Par exemple: 60/4 = 15, 60/5 = 12, 60/12 = 5.
- 15 * (1/4) = 15/60, 12 * (1/5) = 12/60, 5 * (1/12) = 5/60.
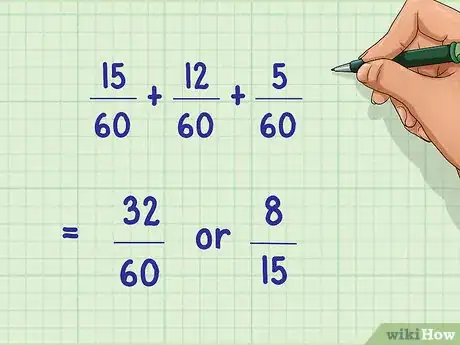
- 15/60 + 12/60 + 5/60.
-
7Solutionnez maintenant le problème. Lorsque vous aurez trouvé le dénominateur commun le plus petit, vous devriez être en mesure de résoudre facilement votre problème. N’oubliez pas de simplifier si possible le résultat que vous obtiendrez.
- Dans notre exemple : 15/60 + 12/60 + 5/60 = 32/60 soit 8/15.
Publicité
Méthode 4
Méthode 4 sur 4:Travailler avec des entiers et des nombres mixtes[7]
Méthode 4
-
1Convertissez vos entiers et nombres mixtes en « pseudofractions ». Faites-le en multipliant le nombre entier par le dénominateur en ajoutant ensuite le numérateur au produit résultant. Vous obtiendrez une pseudofraction en positionnant chacun de vos nombres entiers sur le dénominateur « 1 ».
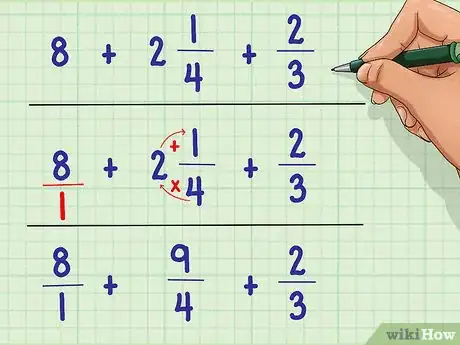
- Exemple: 8 + 2 1/4 + 2/3.
- 8 = 8/1.
- 2 1/4 = 2 * 4 + 1 = 8 + 1 = 9 soit 9/4.
- L’équation reconstituée nous donne : 8/1 + 9/4 + 2/3.
-
2Recherchez le plus petit dénominateur commun. Utilisez l’une des méthodes précédemment décrites pour calculer le plus petit dénominateur commun. Dans cet exemple, vous trouverez le plus petit dénominateur commun en utilisant la méthode décrite plus haut comme « liste des multiples », dans laquelle vous devez établir une liste des multiples de chaque dénominateur.
- Vous n’aurez pas besoin de créer de liste de multiples pour le dénominateur 1, car tout nombre entier est multiple de 1 et conserve sa valeur lorsqu’il est multiplié par ce chiffre.
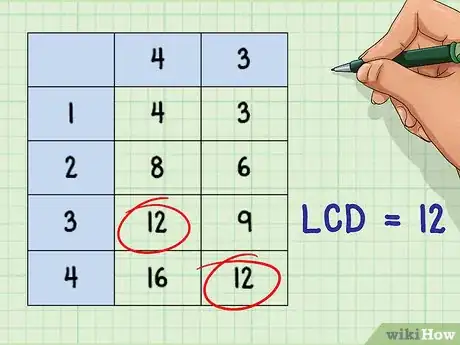
- Exemple : 4 * 1 = 4 ; 4 * 2 = 8 ; 4 * 3 = 12 ; 4 * 4 = 16, et ainsi de suite.
- 3 * 1 = 3 ; 3 * 2 = 6 ; 3 * 3 = 9 ; 3 * 4 = 12 ; etc.
- Le diviseur commun le plus petit est ici égal à 12
-
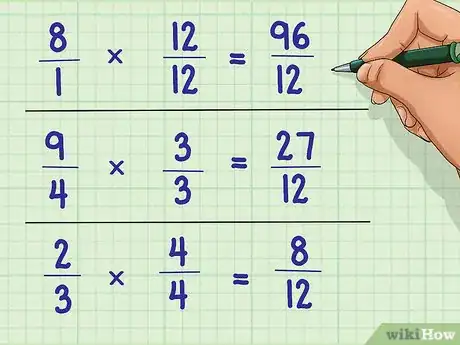
3Revenez maintenant à l’équation initiale. Au lieu de multiplier le dénominateur seul, vous devrez multiplier chaque élément d’une fraction par le chiffre approprié pour transformer votre dénominateur initial en plus petit dénominateur commun.
- Par exemple : (12/12) * (8/1) = 96/12 ; (3/3) * (9/4) = 27/12 ; (4/4) * (2/3) = 8/12.
- 96/12 + 27/12 + 8/12.
-
4Donnez maintenant une solution à votre problème. Lorsque vous aurez trouvé le dénominateur commun le plus petit, vous pourrez facilement le résoudre. N’oubliez pas de simplifier si possible le résultat que vous obtiendrez.
- Exemple: 96/12 + 27/12 + 8/12 = 131/12 soit 10 11/12.
Publicité
Éléments nécessaires
- Un crayon
- Du papier
- Une calculatrice (facultatif)
Références
- ↑ http://www.mathematiquesfaciles.com/fractions-3-reduire-au-meme-denominateur_2_19273.htm
- ↑ http://www.epcc.edu/tutorialservices/valleverde/Documents/Common_Denominators.pdf
- ↑ http://www.aaamath.com/fra66jx2.htm
- ↑ http://www.mathgoodies.com/francais/volume3/gcf_fr.html
- ↑ http://www.helpwithfractions.com/math-homework-helper/least-common-denominator/
- ↑ https://www.mathsisfun.com/prime_numbers.html
- ↑ http://www.calculatorsoup.com/calculators/math/lcd.php#.Ua0eFkDryj4
À propos de ce wikiHow
Mario Banuelos, PhD
Professeur assistant de mathématiques
Cet article a été coécrit par Mario Banuelos, PhD. Mario Banuelos est professeur adjoint de mathématiques à l'université d'État de Californie, à Fresno. Il a plus de huit ans d'expérience dans l'enseignement, et il est spécialisé dans la biologie mathématique, l'optimisation, les modèles statistiques pour l'évolution du génome et la science des données. Mario est titulaire d'une licence en mathématiques de l'université d'État de Californie, Fresno, et d'un doctorat en mathématiques appliquées de l'université de Californie, Merced. Mario a enseigné à la fois au lycée et à l'université. Cet article a été consulté 120 649 fois.
Catégories: Mathématiques
Publicité
