Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 4 868 fois.
Ramener un nombre fractionnaire à sa fraction impropre signifie simplement le transformer en une fraction dont le numérateur est supérieur au dénominateur. Cela fait et si c’est possible, il faut simplifier cette dernière à sa plus simple expression, c’est-à-dire au maximum. La technique est donc toujours la même, et fort simple, même si parfois l’énoncé de l’exercice est un peu différent. Avec de l’entrainement, vous devriez même arriver à faire cette transformation de tête.
Étapes
Partie 1
Partie 1 sur 3:Convertir un nombre fractionnaire en une fraction impropre
-
1Transformez la partie entière du nombre fractionnaire en une fraction. Pour cela, multipliez cette partie par le dénominateur de la fraction existante. Pour rappel, un nombre fractionnaire se compose d’une partie entière (à gauche) et d’une partie fractionnaire (à droite). La partie entière représente le nombre d’éléments d’une référence, tandis que la partie fractionnaire représente une partie d’un seul élément de la même référence. Le dénominateur de la partie fractionnaire indique en combien de parties le tout de référence a été divisé. Si vous multipliez la partie entière par le dénominateur, vous saurez combien de parties du tout de référence sont concernées.
- Pour convertir en fraction, commencez par calculer .
-
2Additionnez les numérateurs. Ainsi, vous additionnez en fait toutes les parts du tout de référence et toutes les parts qui ne forment pas un tout complet. Cette somme sera un nouveau numérateur, celui de la fraction impropre que vous cherchez.
- Dans notre exemple, vous calculerez : . Le numérateur de la fraction impropre est 94.
-
3Ramenez ce numérateur au dénominateur de départ. Le dénominateur ne change pas, seul est modifié le numérateur, lequel est forcément supérieur au dénominateur [1] .
- Le dénominateur de la partie fractionnaire était 16, ce sera aussi celui de la fraction impropre obtenue, au moins temporairement comme on le verra par la suite. C’est ainsi donc que : .
Publicité
Partie 2
Partie 2 sur 3:Simplifier une fraction impropre
-
1Trouvez tous les facteurs du numérateur. Un facteur est une valeur capable de diviser exactement un autre nombre : en fait, c’est un diviseur. Si vous savez faire, vous pouvez utiliser un arbre de facteurs.
- Les facteurs de 94 sont : 1, 2, 47 et 94.
-
2Trouvez tous les facteurs du dénominateur. Opérez de la même façon que pour les diviseurs du numérateur.
- Les facteurs de 16 sont : 1, 2, 4, 8 et 16.
-
3Trouvez le plus grand commun diviseur (PGCD) des deux nombres. Il s’agit tout simplement de trouver un diviseur commun au numérateur et au dénominateur, et s’il y en a plusieurs, le plus grand. [2] . Si vous trouvez un diviseur commun, autre que 1, alors vous pourrez simplifier votre fraction. Si le numérateur et dénominateur n’ont aucun facteur en commun, alors votre fraction ne peut être simplifiée : elle est irréductible.
- Dans notre exemple, malgré le nombre de facteurs, seul 2 est diviseur et c’est le plus grand. La fraction peut donc être divisée par ce PGCD.
-
4Divisez le numérateur et le dénominateur par le PGCD. Vous obtenez une fraction égale à celle du départ, la seule différence est qu’elle est désormais réduite à sa plus simple expression [3] .
- Divisez le numérateur et le dénominateur par 2, ce qui donne respectivement : et . La fraction est irréductible, si bien que vous pouvez écrire que (nombre fractionnaire) est égal à (fraction impropre).
Publicité
Partie 3
Partie 3 sur 3:Faire des conversions de nombres fractionnaires
-
1Transformez en une fraction impropre. La réponse sera une fraction irréductible.
- Multipliez la partie entière par le dénominateur : .
- Additionnez les numérateurs : .
- Placez le nouveau numérateur sur le seul dénominateur connu : .
- Voyez si la fraction peut être simplifiée. Le numérateur et le dénominateur étant des nombres pairs, ils peuvent être, par définition en quelque sorte, au minimum simplifiés par 2.
- La liste des facteurs du numérateur (16) est : 1, 2, 4, 8, 16.
- La liste des facteurs du dénominateur (6) est : 1, 2, 3, 6.
- Identifiez le plus grand commun diviseur. Comme vous le voyez aisément, seul 2 est diviseur et commun, c’est donc le PGCD.
- Divisez le numérateur et dénominateur par le PGCD trouvé : et . La réponse est : .
-
2Donnez comme réponse une fraction impropre. Le libellé est le suivant : au gouter, Juliette a mangé 1 madeleine et comme elle avait encore un peu faim, sa maman lui a donné trois quarts d’une autre madeleine, sinon elle ne mangera rien au repas. Question : combien de madeleines Juliette a-t-elle mangées ?
- Repérez le nombre fractionnaire. Juliette a donc mangé 1 madeleine entière, puis trois quarts d’une autre, elle a donc mangé madeleine.
- Multipliez la partie entière par le dénominateur : .
- Additionnez les numérateurs : .
- Rapportez le nouveau numérateur sur le dénominateur de départ : .
- Voyez si la fraction peut être simplifiée. 7 (nombre premier, uniquement divisible par 1 et lui-même) et 4 n’ont aucun diviseur commun, la fraction est irréductible. Juliette a donc mangé madeleine.
-
3Résolvez la somme suivante : . La première étape consiste donc à convertir chacun des nombres fractionnaires en une fraction impropre.
- Transformez le premier nombre fractionnaire en une fraction impropre : , si bien que la fraction impropre est : .
- Transformez aussi le second nombre fractionnaire en une fraction impropre : . Vous obtenez donc l’égalité suivante :
. - Additionnez les deux fractions.L’addition des fractions obéit à des règles strictes, en particulier, l’obligation d’avoir le même dénominateur. C’est le cas ici, vous pouvez donc additionner leurs numérateurs : . La somme se présente comme suit : .
- Voyez si la fraction peut être simplifiée. Le numérateur et le dénominateur étant des nombres pairs, ils peuvent être simplifiés au minimum par 2.
- Identifiez le plus grand commun diviseur du numérateur et dénominateur. Le PGCD de 12 et 4 est 4.
- Divisez le numérateur et le dénominateur par le PGCD : et . La nouvelle fraction est donc : , c’est-à-dire 3.
Publicité
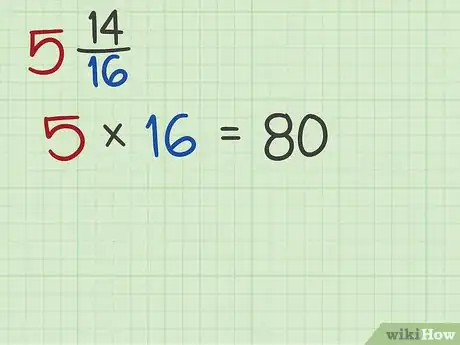


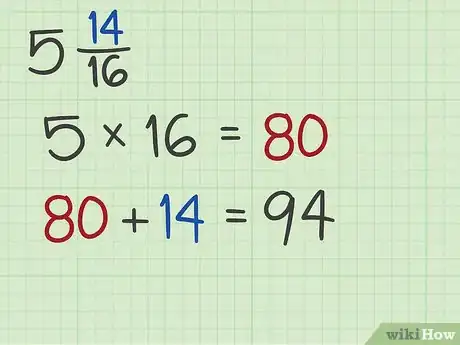

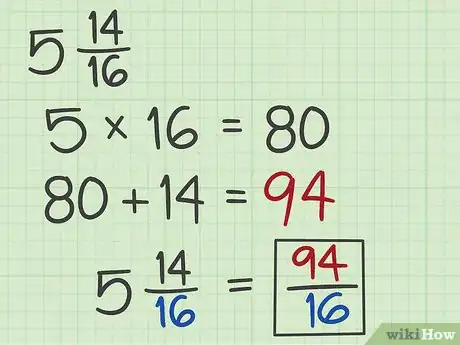


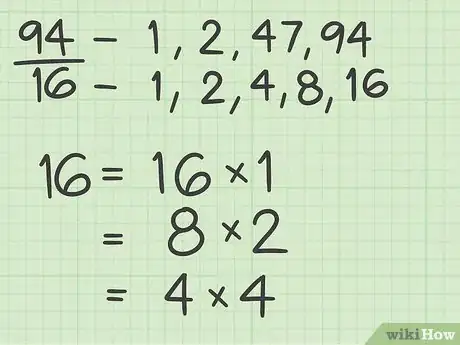





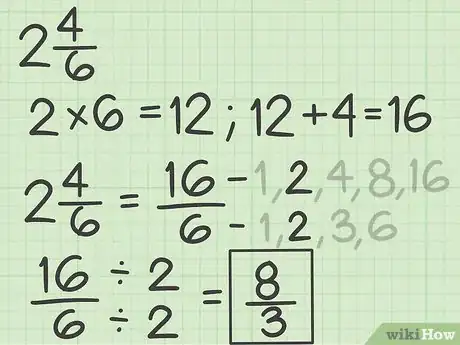









































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 4 868 fois.