Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 61 849 fois.
Quand on aborde en cours d'algèbre la résolution des équations, on débute toujours par des équations simples avec une seule inconnue, d'un seul côté de l'équation. Plus tard, les choses se corsent quand apparaissent des équations avec des inconnues des deux côtés dans les deux membres. La chose la plus importante à retenir quand on cherche à résoudre une équation est de souvenir que lorsqu’on opère un changement sur un des membres, il faut opérer le même changement sur l'autre membre. Si vous assimilez bien cette règle, vous pourrez résoudre toutes les équations.
Étapes
Méthode 1
Méthode 1 sur 3:Résoudre des équations avec une même inconnue dans chaque membre
-
1Développez éventuellement les produits. On utilise pour cela la distributivité de la multiplication sur l'addition, à savoir que [1] . L'intérêt d'agir ainsi est de faire disparaitre les parenthèses : on multiplie chacun des termes de l'addition par le coefficient situé devant [2] .
- Prenons l'équation : . Grâce la la distributivité de la multiplication, on multiplie à gauche, chaque terme de l'addition par 2, et à droite, par 4, ce qui donne :
- Prenons l'équation : . Grâce la la distributivité de la multiplication, on multiplie à gauche, chaque terme de l'addition par 2, et à droite, par 4, ce qui donne :
-
2Isolez l'inconnue. Cela consiste à n'avoir l'inconnue que d'un seul côté de l'équation. Pour cela, il suffit d'ajouter aux deux membres de l'équation le terme opposé au terme contenant . Si le terme est précédé d'un signe « - », on ajoutera le même terme précédé d'un signe « + ». S'il est précédé d'un « + », on ajoutera le même terme avec le signe « - ». Habituellement, on fait disparaitre le terme dont le coefficient est le plus petit.
- Ainsi, dans l'équation , on va fait faire disparaitre le terme en ajoutant à gauche :
.
- Ainsi, dans l'équation , on va fait faire disparaitre le terme en ajoutant à gauche :
-
3Ne déséquilibrez pas l'équation. Quand on opère un changement sur un des membres, il faut opérer le même changement sur l'autre membre. Ainsi, si vous ajoutez ou soustrayez une quantité d'un côté, vous devez faire exactement la même chose de l'autre, le but étant de faire disparaitre l'inconnue d’un côté.
- Ainsi, comme on a ajouté d'un côté de l'équation (à gauche), on fait la même chose dans le membre de droite, ce qui donne :
- Ainsi, comme on a ajouté d'un côté de l'équation (à gauche), on fait la même chose dans le membre de droite, ce qui donne :
-
4Simplifiez l'équation. Additionnez les termes de même puissance. Vous avez alors une équation avec l'inconnue d'un seul côté et une valeur numérique de l'autre côté.
- Dans notre exemple, on a :
- Dans notre exemple, on a :
-
5Regroupez éventuellement les constantes. Faites les passer d'un côté de l'équation. Le but consiste en effet à faire passer l'inconnue d'un côté de l'équation, et toutes les constantes de l'autre. Ainsi, il sera plus facile de déterminer l'inconnue. Pour déplacer une constante, il suffit de lui ajouter sa valeur opposée. Ce faisant, il faut faire la même chose dans l'autre membre de l'équation [3] .
- Ainsi, pour faire passer le de notre équation de l'autre côté, il faut soustraire 8 des deux côtés, ce qui donne :
- Ainsi, pour faire passer le de notre équation de l'autre côté, il faut soustraire 8 des deux côtés, ce qui donne :
-
6Faites disparaitre le coefficient de l'inconnue. Un coefficient est une valeur numérique qui multiplie une inconnue. Pour s'en débarrasser, il faut diviser le terme contenant par la valeur du coefficient en question (ou on multiplie par son inverse). On fait la même chose sur l'autre membre de l'équation [4] . Rappelez-vous que si vous opérez un changement sur un des membres, vous devez opérer le même changement sur l'autre membre.
- Ainsi, pour faire disparaitre le 12 de , on divise les deux membres de l'équation par 12, ce qui donne l'égalité suivante :
- Ainsi, pour faire disparaitre le 12 de , on divise les deux membres de l'équation par 12, ce qui donne l'égalité suivante :
-
7Vérifiez vos calculs. Pour cela, il suffit de remplacer dans l'équation d'origine la valeur de que vous venez de trouver. Si, après calculs, l'égalité est vérifiée, c'est que vous avez tout juste.
- Ainsi, vous avez précédemment trouvé que . Vous remplacez alors par 1 dans l'équation de départ, et vous faites vos calculs :
Publicité - Ainsi, vous avez précédemment trouvé que . Vous remplacez alors par 1 dans l'équation de départ, et vous faites vos calculs :
Méthode 2
Méthode 2 sur 3:Résoudre un système d'équations à deux inconnues
-
1Isolez une inconnue dans une des équations. Dans certains systèmes, l'inconnue sera déjà isolée. Si ce n'était pas le cas, en utilisant certaines règles d'algèbre, isolez une des inconnues : elle sera toujours fonction de l'autre inconnue. Parmi ces règles, rappelons celle qui veut que si vous opérez un changement sur un des membres, vous devez effectuer le même changement sur l'autre membre.
- Résolvez le système suivant : . Prenez la première équation (). Pour isoler , vous devez soustraire 1 des deux côtés de l'équation, ce qui donne :
- Résolvez le système suivant : . Prenez la première équation (). Pour isoler , vous devez soustraire 1 des deux côtés de l'équation, ce qui donne :
-
2Remplacez cette inconnue dans la seconde équation. Ce faisant, faites bien attention à la remplacer par la valeur que vous venez de trouver. Vous allez vous retrouver avec une seconde équation qui ne contiendra qu'une seule inconnue, ce qui vous permettra de la calculer [5] .
- Pour mémoire, la seconde équation est : , et vous avez trouvé que : . Si vous remplacez dans cette équation par , vous obtenez :
- Pour mémoire, la seconde équation est : , et vous avez trouvé que : . Si vous remplacez dans cette équation par , vous obtenez :
-
3Trouvez l'inconnue. Pour cela, déplacez l'inconnue d'un côté de l'équation, déplacez toutes les constantes de l'autre, puis faites disparaitre le coefficient en multipliant ou en divisant.
- Pour notre exemple, on a :
- Pour notre exemple, on a :
-
4Trouvez la seconde inconnue. Rien de plus facile : dans une des deux équations, peu importe laquelle, remplacez l'inconnue dont vous venez de trouver la valeur. À nouveau, vous vous retrouvez avec une équation avec une seule inconnue, mais c'est la seconde. Comme précédemment, déplacez l'inconnue d'un côté de l'équation, déplacez toutes les constantes de l'autre, puis faites disparaitre le coefficient en multipliant ou en divisant. Vous obtenez votre dernière inconnue.
- Vous avez précédemment trouvé que , remplacez dans la seconde équation par cette valeur de 6 :
- Vous avez précédemment trouvé que , remplacez dans la seconde équation par cette valeur de 6 :
-
5Vérifiez vos calculs. Remplacez et par leurs valeurs respectives dans une des équations. Si, après calculs, l'égalité est vérifiée, c'est que vous avez tout juste.
- Vous avez donc trouvé que et , remplacez ces deux valeurs dans l'équation de départ, ce qui vous donne :
Publicité - Vous avez donc trouvé que et , remplacez ces deux valeurs dans l'équation de départ, ce qui vous donne :
Méthode 3
Méthode 3 sur 3:Résoudre quelques équations
-
1Résolvez l'équation à une inconnue suivante. Résolvez-la en utilisant la distributivité de la multiplication :
- Développez le produit du premier membre pour ne plus avoir de parenthèses :
- Supprimez le de gauche en soustrayant des deux côtés de l'équation. On obtient donc :
ou
- Isolez votre inconnue en ajoutant 5 des deux côtés de l'équation, ce qui donne :
ou
- Développez le produit du premier membre pour ne plus avoir de parenthèses :
-
2Résolvez une équation contenant une fraction. Résolvez l'équation suivante :
- Débarrassez-vous du dénominateur. Pour cela, il suffit de multiplier de chaque côté par la valeur du dénominateur, ce qui donne ici :
- Regroupez les à gauche. Pour cela, il suffit d'ajouter de chaque côté. Vous obtenez alors :
- Regroupez toutes les constantes à droite. Il suffit dans ce cas d'ajouter 14 de chaque côté, ce qui donne :
- C'est presque terminé. Supprimez le coefficient de en divisant de chaque côté par 7 :
- Débarrassez-vous du dénominateur. Pour cela, il suffit de multiplier de chaque côté par la valeur du dénominateur, ce qui donne ici :
-
3Résolvez un système d'équations. Résolvez le système suivant :
- Pour commencer, exprimez avec dans la seconde équation :
- Remplacez, dans la seconde équation, par . Vous obtenez :
- Développez le membre de droite en utilisant la distributivité de la multiplication :
- Regroupez tous les à droite de l'équation. Pour cela, soustrayez de chaque côté de l'équation. Vous avez alors :
- Regroupez toutes les constantes à gauche de l'équation en soustrayant 36 de chaque côté de l'équation, ce qui donne :
- Isolez en divisant de chaque côté par 3. Vous obtenez l'égalité suivante :
, soit - Trouvez désormais en remplaçant, par exemple dans la seconde équation, par la valeur trouvée. L'équation se présente ainsi :
Publicité - Pour commencer, exprimez avec dans la seconde équation :
Éléments nécessaires
- Un crayon
- Du papier
- Une calculatrice
Références
- ↑ http://www.coolmath.com/prealgebra/06-properties/05-properties-distributive-01
- ↑ http://www.virtualnerd.com/algebra-1/linear-equations-solve/variables-both-sides-equations/variables-both-sides-solution/variables-grouping-symbols-both-sides
- ↑ http://www.algebralab.org/studyaids/studyaid.aspx?file=Algebra1_3-3.xml
- ↑ http://www.algebralab.org/studyaids/studyaid.aspx?file=Algebra1_3-3.xml
- ↑ http://www.virtualnerd.com/pre-algebra/linear-functions-graphing/system-of-equations/solving-systems-equations/two-equations-two-variables-substitution
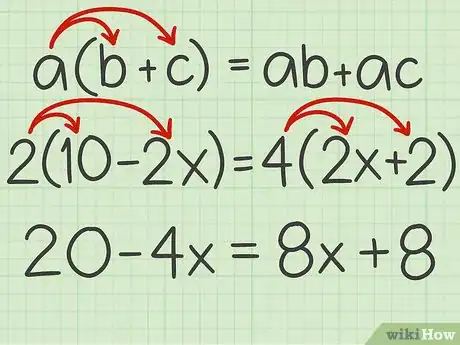



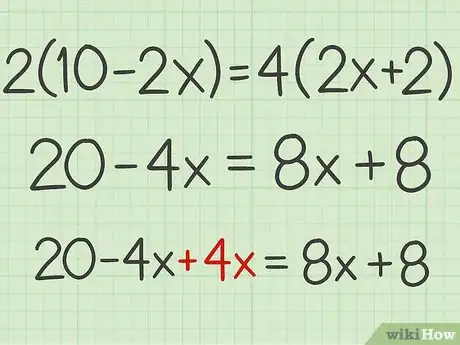




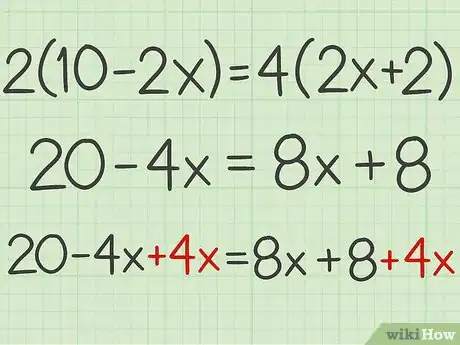

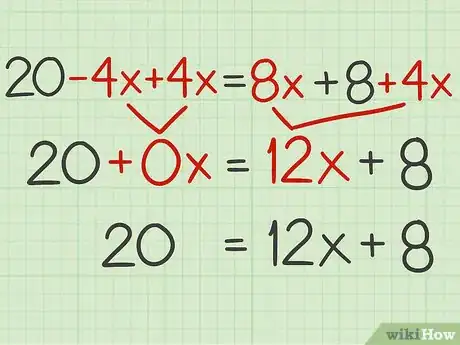

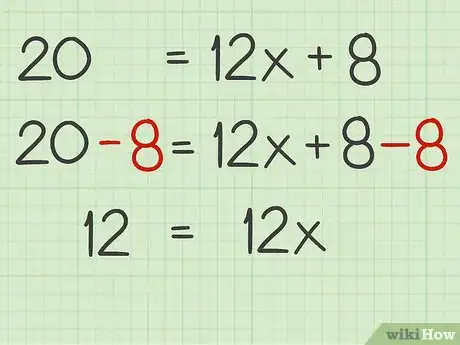



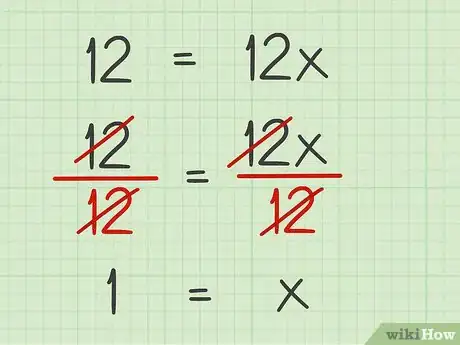



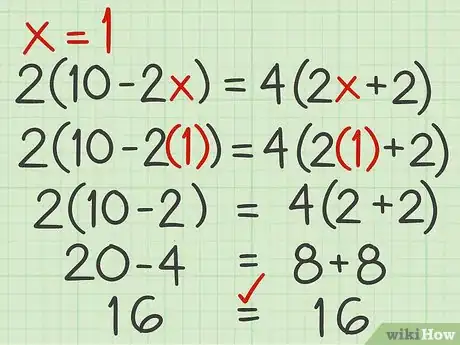





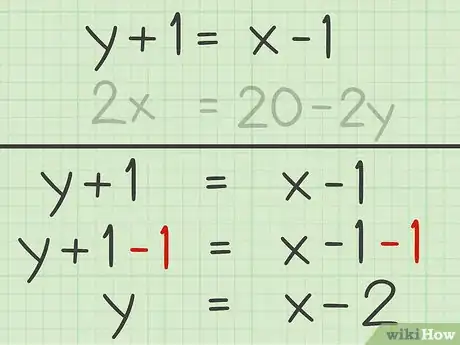









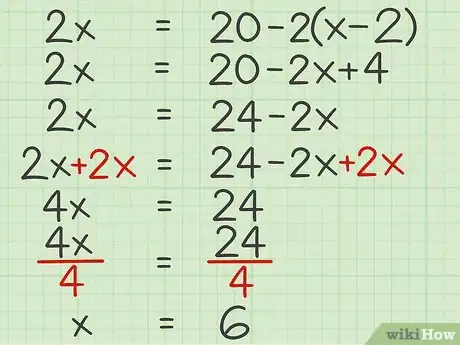






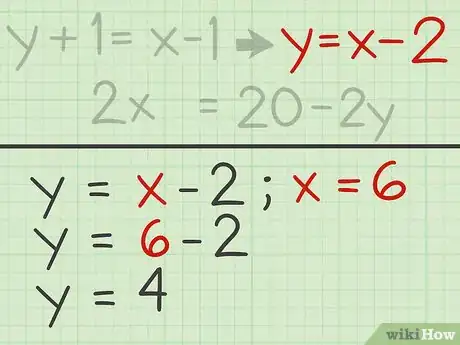


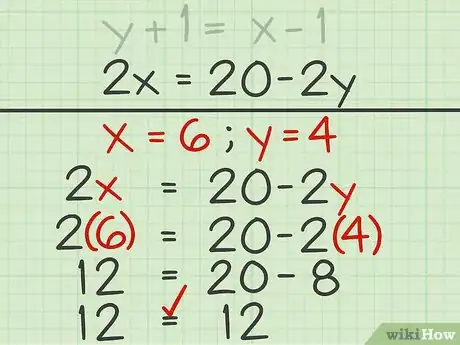



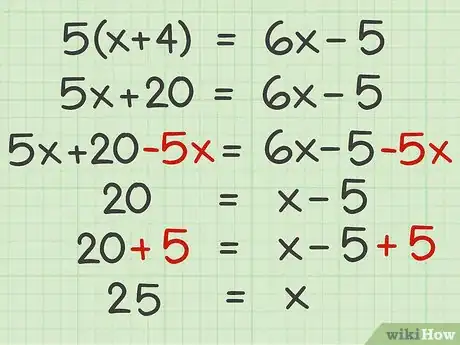





























































L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 61 849 fois.