Comment se servir d'une règle à calcul

Pour quelqu’un qui n’aurait jamais vu de règle de calcul de sa vie, cet instrument ressemble fort à un casse-tête numérique. À première vue, on identifie déjà au moins trois échelles différentes (voire beaucoup plus !) et on remarque rapidement que les graduations ne sont pas espacées de façon égale. Quand vous aurez appris à le manipuler, vous comprendrez pourquoi cet instrument a été fort utile depuis le XVIIe siècle, et ce, jusqu’à l’invention des calculatrices dans les années 1970. En alignant correctement les nombres à multiplier et avec de la pratique, vous allez voir qu’on peut faire des multiplications très rapidement, beaucoup plus vite qu’à la main.

Partie 1
Partie 1 sur 4:
Comprendre ce qu’est une règle à calcul

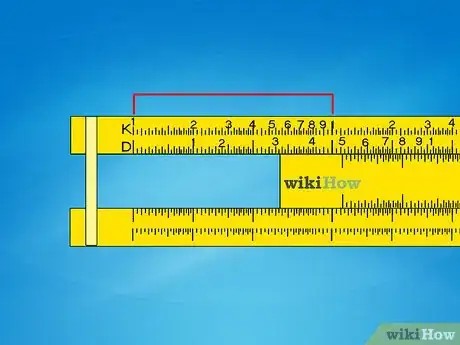
  1. Image intitulée Use a Slide Rule Step 1
    1
    Remarquez les intervalles entre les graduations. À la différence d’une règle classique, les graduations d’une règle à calcul ne sont pas espacées de façon régulière, selon une progression linéaire. En effet, ce sont des graduations inégales de type « logarithmique ». En alignant ces échelles, vous pourrez faire toutes les multiplications que vous voulez, comme on va le voir.
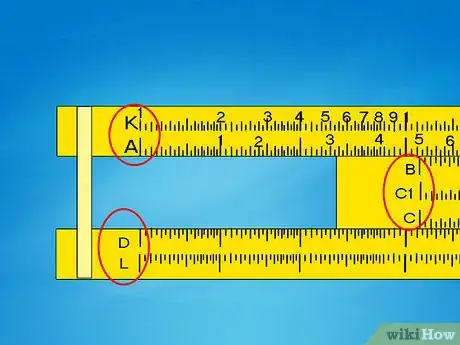
  2. Image intitulée Use a Slide Rule Step 2
    2
    Repérez les appellations des différentes échelles. Chaque échelle de la règle à calcul est repérée par une lettre ou un symbole, soit à droite, soit à gauche. Nous allons vous décrire les principales échelles d’une règle à calcul courante [1]  :
    • les échelles C et D (de 1 à 10) se lisent de gauche à droite et il n’y a qu’une seule graduation continue. Ce sont les échelles des « unités ».
    • les échelles A et B (de 1 à 100) sont celles des « dizaines ». Chacune d’elles comporte deux séries de graduations mises bout à bout.
    • l’échelle K (de 1 à 1000) est celle des « cubes ». Elle est composée de trois séries de graduations mises bout à bout. Elle n’existe pas sur toutes les règles.
    • les échelles C|et D|sont similaires aux échelles C et D, mais elles se lisent de droite à gauche. Elles sont le plus souvent en rouge, mais n’existent pas sur toutes les règles.
    • Notez que les règles de calcul varient, de sorte que les échelles marquées C et D sur votre règle peuvent ne pas être les mêmes que celles décrites ici. Sur certaines règles, les échelles utilisées pour la multiplication sont marquées A et B et se trouvent en haut. Quelle que soit la lettre de désignation, ces échelles ont souvent le symbole Pi marqué à l’endroit approprié et sont presque toujours les deux échelles opposées sur les diapositives, soit l’écart supérieur ou inférieur. Il est suggéré d’essayer quelques problèmes de multiplication simples pour vérifier que vous utilisez la bonne échelle comme il a été décrit dans l’article. Si 2 x 4 n’aboutit pas à 8, essayez plutôt les échelles de l’autre côté de la règle.
  3. Image intitulée Use a Slide Rule Step 3
    3
    Sachez lire les divisions des échelles. Repérez les traits verticaux des échelles C et D et sachez ce qu’ils représentent.
    • L’échelle démarre à 1 à gauche, va jusqu’à 9 et se termine par un 1 sur le bord droit. Tous les chiffres entre 1 et 9 sont indiqués. Ce sont les divisions primaires.
    • Les divisions secondaires, traits légèrement plus courts que ceux des divisions primaires, représentent les dixièmes (0,1). Faites attention ! S’ils sont marqués « 1, 2, 3 », il faut bien comprendre qu’ils signifient, s’ils sont entre le 1 et le 2, « 1,1, 1,2, 1,3 », etc.
    • Il y a aussi des divisions encore plus petites, qui correspondent à des intervalles de 0,02, mais elles disparaissent complètement au bout de l’échelle quand les graduations tendent à se resserrer.
  4. Image intitulée Use a Slide Rule Step 4
    4
    Ne vous attendez pas à avoir des réponses très précises ! Au moment de la lecture, vous aurez le plus souvent à faire la « meilleure évaluation possible » si le curseur tombe entre deux graduations. Une règle à calcul sert à faire rapidement des opérations qui ne réclament pas une très grande précision.
    • Ainsi, si la ligne du curseur se situe entre 6,51 et 6,52, prenez comme réponse ce qui vous semble le plus logique, sinon mettez 6,515.
    Publicité

Partie 2
Partie 2 sur 4:
Multiplier des nombres

  1. Image intitulée Use a Slide Rule Step 5
    1
    Posez votre multiplication. Inscrivez les deux nombres à multiplier.
    • Le 1er exemple que nous utiliserons ici, consiste à calculer 260 x 0,3.
    • Le 2e exemple consistera à calculer 410 x 9. Cette opération est un peu plus compliquée que celle du 1er exemple, aussi est-il préférable de commencer par cette dernière.
  2. Image intitulée Use a Slide Rule Step 6
    2
    Déplacez la virgule de chacun des nombres à multiplier. La règle à calcul ne comprenant que des chiffres entiers (entre 1 et 10), déplacez les virgules de vos nombres à multiplier de façon à avoir une valeur qui tombe entre ces deux limites. La virgule finale sera placée après le calcul, comme on le verra à la fin de cette partie.
    • 1er exemple : pour calculer 260 (ou 260,0) x 0,3 sur une règle à calcul, on va faire en fait 2,6 x 3.
    • 2e exemple : pour calculer 410 (ou 410,0) x 9, on va faire 4,1 x 9.
  3. Image intitulée Use a Slide Rule Step 7
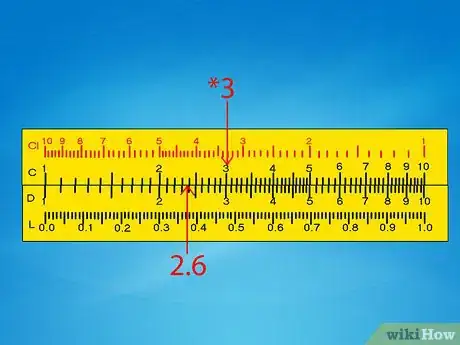
    3
    Repérez le plus petit nombre sur l’échelle D. Puis, alignez avec l’échelle C. Commencez par repérer le plus petit nombre sur l’échelle D. Faites coulisser la règle mobile avec l’échelle C de façon à aligner le « 1 » de cette échelle avec la valeur de l’échelle D.
    • 1er exemple : faites glisser l’échelle C de façon à aligner le 1 avec le 2,6 de l’échelle D.
    • 2e exemple : faites glisser l’échelle C de façon à aligner le 1 avec le 4,1 de l’échelle D.
  4. Image intitulée Use a Slide Rule Step 8
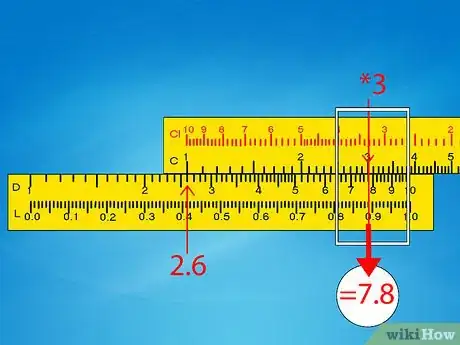
    4
    Faites glisser le curseur jusqu’au second nombre à multiplier sur l’échelle C. Le curseur est cette partie transparente qui coulisse sur la règle. Alignez le trait rouge du curseur sur le second nombre visible sur l’échelle C. La réponse est alors lisible sur le trait rouge, mais sur l’échelle D. Si la réponse est hors de la règle, allez à la partie suivante.
    • 1er exemple : placez le curseur sur le 3 de l’échelle C. Le trait rouge vous indique alors, à peu de chose près, 7,8 sur l’échelle D. Allez à l’étape 6 pour la détermination du résultat.
    • 2e exemple : essayez de placer le curseur sur le 9 de l’échelle C. Sur la plupart des règles, ce sera une mission impossible, car le curseur se retrouvera dans le vide à l’extrémité de l’échelle D. Voyez l’étape suivante pour régler ce problème.
  5. Image intitulée Use a Slide Rule Step 9
    5
    Servez-vous du repère « 1 » situé à droite de l’échelle. Vous devrez le faire si le curseur ne peut donner la réponse. Si le curseur est bloqué au centre de la règle ou si la réponse se situe « en dehors de la règle », il faut procéder légèrement différemment [2] . Alignez le « 1 » situé à droite de l’échelle C avec le plus grand des deux nombres, situé sur la règle de l’échelle D. Faites glisser le curseur et alignez sur l’échelle C, le trait sur le second nombre. Le résultat sera lu sur l’échelle D.
    • 2e exemple : faites glisser l’échelle C en sorte que le « 1 » de droite soit aligné avec le 9 de l’échelle D. Faites glisser le curseur sur 4,1 sur l’échelle C. Le curseur indique sur l’échelle D une valeur comprise entre 3,68 et 3,7 : la valeur est donc d’environ 3,69.
  6. Image intitulée Use a Slide Rule Step 10
    6
    Vous devez recourir à l’estimation pour trouver le résultat définitif. Quelle que soit la multiplication, vous aurez toujours une réponse temporaire comprise entre 1 et 10, puisque vous la lisez sur l’échelle D, laquelle va de … 1 à 10 ! Comme vous n’avez que les chiffres significatifs, il faut estimer le résultat en faisant un peu de calcul mental.
    • 1er exemple : notre opération de départ était 260 x 0,3. La règle à calcul nous a donné une réponse, à savoir 7,8. Trouvez une opération proche en arrondissant les deux éléments du produit et effectuez-la mentalement. Ici, on fera : 250 x 0,5 = 125. Cette réponse est plus proche de 78 que de 780, donc la réponse est 78.
    • 2e exemple : notre opération de départ était 410 x 9. La règle à calcul nous a donné une réponse, à savoir 3,69. Faites mentalement : 400 x 10 = 4000. Assez logiquement, votre réponse est 3690, la plus proche de 4000.
    Publicité

Partie 3
Partie 3 sur 4:
Calculer des carrés et des cubes

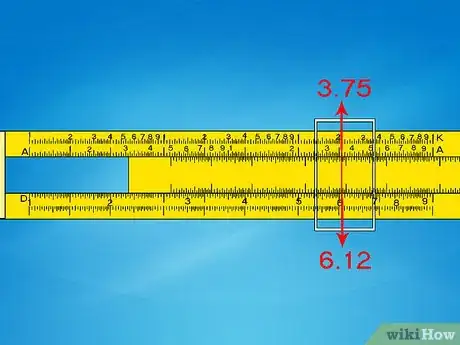
  1. Image intitulée Use a Slide Rule Step 11
    1
    Servez-vous des échelles D et A pour calculer les carrés. Ces deux échelles sont fixes. Si vous mettez le trait du curseur sur une valeur de l’échelle D, vous lirez son carré sur l’échelle A [3] . Comme pour le produit, il faut là encore, faire une estimation pour placer la virgule.
    • Ainsi, pour calculer 6,12, placez le curseur sur 6,1 sur l’échelle D. Sur l’échelle A, vous lisez 3,75.
    • Estimez la valeur de 6,12 en la rapprochant de à 6 x 6 = 36. Déplacez la virgule pour obtenir la valeur la plus proche de 36, soit 37,5.
    • La réponse exacte est 37,21. La règle à calcul donne des résultats fiables dans la limite de 1%, précision largement suffisante dans la vie de tous les jours !
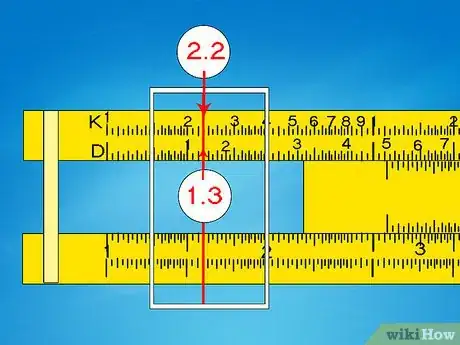
  2. Image intitulée Use a Slide Rule Step 12
    2
    Servez-vous des échelles D et K pour calculer les cubes. Nous venons de voir que l’échelle A, qui est une échelle D réduite au 1/2, permet de trouver les carrés des nombres. De la même façon, l’échelle K, qui est une échelle D réduite au 1/3, permet de trouver les cubes des nombres. Placez le curseur sur une valeur de l’échelle D et lisez le résultat sur l’échelle K. Comme précédemment, recourez à l’estimation pour placer correctement la virgule et déterminer la réponse exacte.
    • Ainsi, pour calculer 1303, placez le curseur sur le 1,3 de l’échelle D. Sur l’échelle K, vous lisez 2,2. Comme 1003 = 1 x 106 et 2003 = 8 x 106, vous savez que votre réponse sera entre ces valeurs. La seule réponse possible est alors 2,2 x 106, soit 2 200 000.
    Publicité

Partie 4
Partie 4 sur 4:
Calculer des racines carrées et cubiques

  1. Image intitulée Use a Slide Rule Step 13
    1
    Avant toute chose, écrivez le radicande en notation scientifique. Comme cela a été dit plusieurs fois, la règle à calcul ne renvoie que des résultats compris entre 1 et 10. Vous devez donc écrire le radicande en notation scientifique pour pouvoir trouver la racine carrée.
    • 3e exemple : pour trouver √(390), récrivez-la sous la forme √(3,9 x 102).
    • 4e exemple : pour trouver √(7100), récrivez-la sous la forme √(7,1 x 103).
  2. Image intitulée Use a Slide Rule Step 14
    2
    Déterminez le côté de l’échelle A à utiliser. Afin de trouver une racine carrée, il faut d’abord faire glisser le curseur sur le radicande situé sur l’échelle A. Comme l’échelle A compte deux intervalles, respectivement [1 ; 10] et [10 ; 100], il vous appartient de savoir lequel prendre [4] . Voici comment on procède :
    • si l’exposant est pair (102 du 3e exemple), servez-vous du côté gauche de l’échelle A (intervalle [1 ; 10]) ;
    • si l’exposant est impair (103 du 4e exemple), servez-vous du côté droit de l’échelle A (intervalle [10 ; 100]).
  3. Image intitulée Use a Slide Rule Step 15
    3
    Faites glisser le curseur sur l’échelle A. En laissant de côté pour l’instant la puissance de 10, placez le curseur sur le nombre significatif trouvé et situé sur l’échelle A.
    • 3e exemple : pour calculer √(3,9 x 102), placez le curseur sur le 3,9 de l’intervalle gauche de A (parce que l’exposant est pair).
    • 4e exemple : pour calculer √(7,1 x 103), placez le curseur sur le 7,1 de l’intervalle droit de A (parce que l’exposant est impair).
  4. Image intitulée Use a Slide Rule Step 16
    4
    Lisez la réponse sur l’échelle D. Lisez sous le trait du curseur et sur l’échelle D, votre réponse. Ajoutez « x 10n » à cette valeur. Afin de déterminer « n », prenez l’exposant de la puissance de 10 de votre radicande, arrondissez-le, s’il est impair, au nombre pair immédiatement inférieur et divisez par 2.
    • 3e exemple : la valeur de l’échelle D qui correspond à 3,9 de l’échelle A est d’environ 1,975. Avec la notation scientifique, on avait 102. 2 étant déjà pair, il suffit de le diviser par 2 pour obtenir 1. La réponse définitive est donc : 1,975 x 101 ou 19,75.
    • 4e exemple : la valeur de l’échelle D qui correspond à 7,1 de l’échelle A est d’environ 8,45. Avec la notation scientifique, on avait 103. 3 étant impair, on l’arrondit au nombre pair immédiatement inférieur, soit 2, qu’on divise par 2, soit 1. La réponse définitive est donc : 8,45 x 101 ou 84,5.
  5. Image intitulée Use a Slide Rule Step 17
    5
    Pour les racines cubiques, procédez de même, mais avec l’échelle K. La technique pour les racines cubiques est similaire à la précédente. Le plus important, ici, est de déterminer laquelle des trois échelles K il faut prendre en compte. Pour cela, il faut diviser le nombre de chiffres qui composent votre nombre, puis le diviser par trois et enfin étudier le reste. C’est simple : si le reste est 1, vous prenez la première échelle ; si le reste est 2, vous prenez la deuxième et si le reste est 3, vous prenez la troisième. On peut aussi compter, avec le doigt, les échelles directement sur la règle. Quand vous arrivez au nombre de chiffres, vous avez votre échelle de lecture [5] .
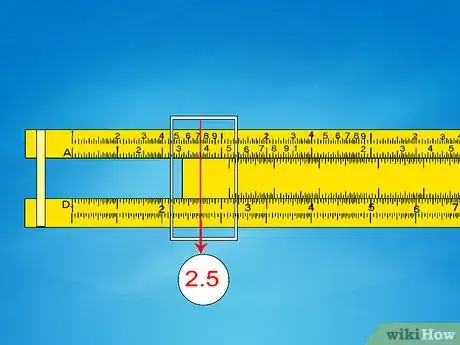
    • 5e exemple : pour trouver la racine cubique de 74 000, comptez d’abord le nombre de chiffres (5), divisez-le par 3 et prenez le reste (il y va 1 fois et il reste 2). Comme le reste est de 2, servez-vous de la deuxième échelle (avec la « méthode du doigt », vous comptez cinq échelles : 1–2–3–1–2 ).
    • Faites glisser le curseur sur le 7,4 de la deuxième échelle K. Sur l’échelle D, vous lisez alors environ 4,2.
    • Étant donné que 103 est inférieur à 74 000, mais que 1003 est supérieur à 74 000, la réponse se situe forcément entre 10 et 100. Déplacez la virgule en conséquence et vous obtenez 42.
    Publicité

Conseils

  • Il est possible de se livrer à d’autres opérations avec une règle à calcul, en particulier si elle comprend des échelles dites « log-log » (LL2 ou LL3), des échelles pour le calcul trigonométrique ou d’autres échelles spécifiques. Consultez le mode d’emploi de la règle ou faites des recherches sur Internet pour en savoir plus sur ces échelles.
  • Maintenant que vous savez multiplier, vous allez pouvoir convertir des unités de mesure. Ainsi, sachant que 1 pouce = 2,54 centimètres, vous allez pouvoir savoir combien font 5 pouces. Il suffit de faire : 5 x 2,54. À votre règle !
  • La précision d’une règle à calcul dépend de la précision des graduations. Plus une règle est longue, plus grande est la précision.
Publicité

Avertissements

  • Conservez votre règle à calcul à l’abri de la chaleur et de l’humidité. Elle risquerait de se déformer dans un sens ou dans un autre, ce qui entrainerait de fausses lectures [6] .
Publicité

wikiHows en relation

convertir un nombre binaire en nombre décimal
Comment
convertir un nombre binaire en nombre décimal
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
Comment
convertir un nombre hexadécimal en nombre binaire ou en nombre décimal
trouver le sommet d'une parabole d'une équation du second degré
Comment
trouver le sommet d'une parabole d'une équation du second degré
calculer une racine carrée sans calculatrice
Comment
calculer une racine carrée sans calculatrice
convertir des degrés en radians
Comment
convertir des degrés en radians
utiliser la méthode 3 4 5 pour construire des angles droits
Comment
utiliser la méthode 3 4 5 pour construire des angles droits
convertir des radians en degrés
Comment
convertir des radians en degrés
convertir des secondes en minutes
Comment
convertir des secondes en minutes
convertir les minutes en heures
Comment
convertir les minutes en heures
convertir du décimal en binaire
Comment
convertir du décimal en binaire
se souvenir de la table trigonométrique
Comment
se souvenir de la table trigonométrique
simplifier une racine carrée
Comment
simplifier une racine carrée
factoriser un polynôme du troisième degré
Comment
factoriser un polynôme du troisième degré
convertir des secondes en heures
Comment
convertir des secondes en heures
Publicité

Références

  1. ↑ http://sliderulemuseum.com/SR_Course.htm
  2. ↑ http://sliderulemuseum.com/SR_Course.htm
  3. ↑ http://www.sliderules.info/a-to-z/tys/tys03.htm#A%20and%20B%20Scales
  4. ↑ http://www.sliderules.info/a-to-z/tys/tys03.htm#A%20and%20B%20Scales
  5. ↑ http://www.antiquark.com/sliderule/sim/sr-calcs-by-example.html#mozTocId734623
  6. ↑ http://www.sliderules.info/a-to-z/tys/tys03.htm

À propos de ce wikiHow

wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 10 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps. Cet article a été consulté 16 253 fois.
Catégories: Mathématiques
Publicité