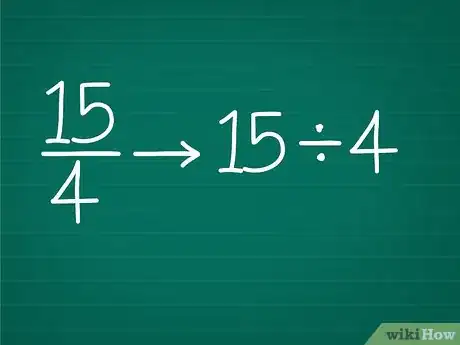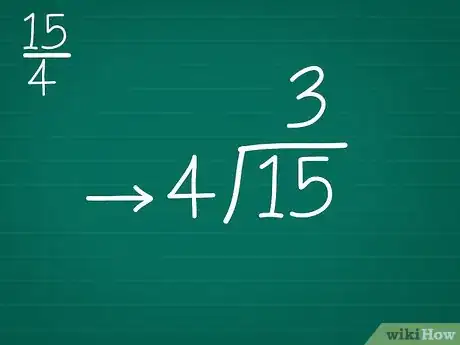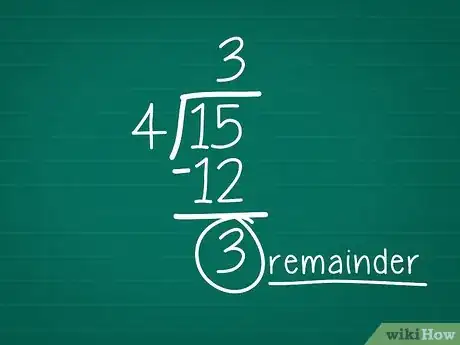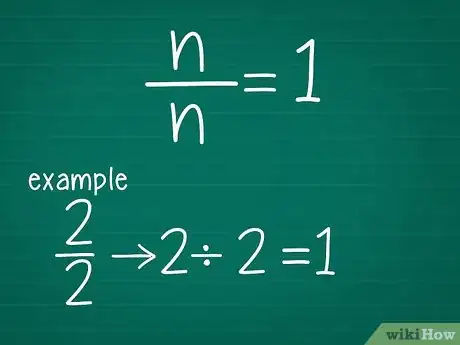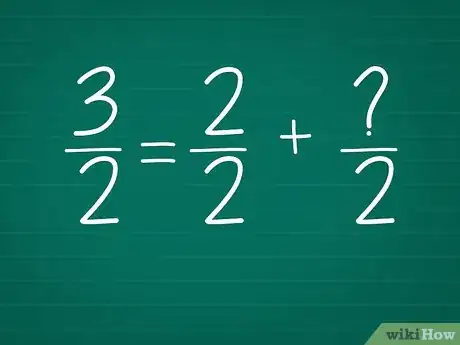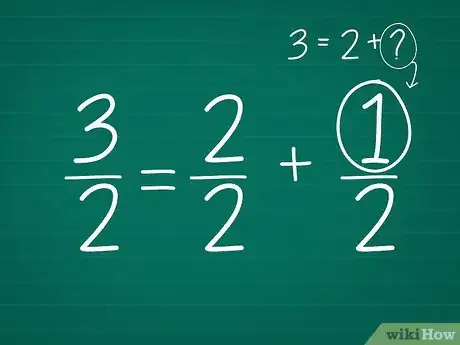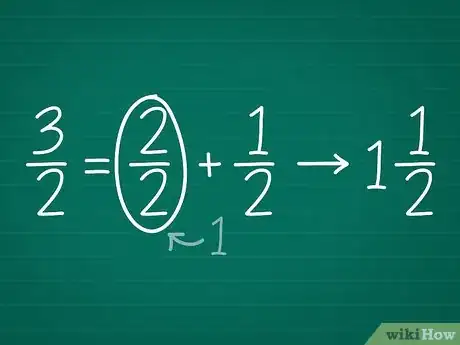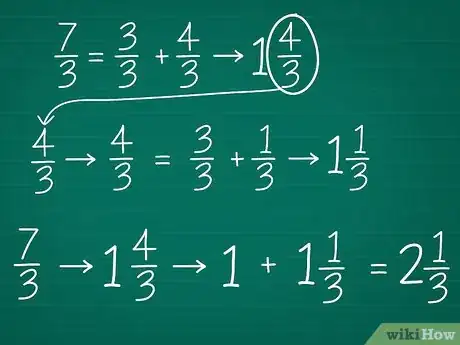wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, des auteur.e.s volontaires ont participé à l'édition et à l'amélioration.
Cet article a été consulté 7 647 fois.
Une fraction impropre est une fraction dont le chiffre (ou le nombre) du haut est supérieur à celui du bas, à l'image de 5/2. Un nombre mixte est un nombre entier, suivi d'une partie fractionnaire, comme 21/2. Notez qu'il est plus facile de dire 21/2 pizzas que cinq moitiés de pizza. Vous le voyez, il est parfois utile de passer des fractions impropres aux nombres mixtes [1] . On peut certes en passer par la division pour arriver à cette transformation, mais il existe une autre méthode peut-être plus simple si vous ne maitrisez pas bien la division.
Étapes
Méthode 1
Méthode 1 sur 2:Faire une division
-
1Partez d'une fraction impropre. On prendra comme exemple : 15/4. C'est bien une fraction impropre, puisque le numérateur, 15, est supérieur au dénominateur, 4.
- Si vous n'êtes pas très à l'aise avec les fractions ou les divisions, essayez cette méthode.
-
2Transformez cette fraction en division. Posez l'opération, à savoir une division [2] . Attention à l'ordre ! C'est le numérateur qu'on divise par le dénominateur. Dans notre exemple, ce sera : 15 ÷ 4.
-
3Commencez la division. Si vous avez oublié, relisez cet article pour savoir comment on fait une division [3] . Pour vous aider, vous pouvez écrire la démarche ainsi :
- je prends 1, et je me demande combien il y va de fois 4, la réponse est 0, donc je prends 15 ;
- je prends 15, et je me demande combien il y va de fois 4. Si vous ne maitrisez pas trop la multiplication, lisez cet article ;
- la réponse est 3. Inscrivez ce 3 sous la barre de division, en dessous du 4 en somme.
-
4Trouvez le reste. À moins que vous n'obteniez un résultat rond, il y a toujours un reste. Voici comment on trouve ce reste [4] :
- multipliez votre réponse par le diviseur (valeur au-dessus de la barre de division). Dans notre exemple, c'est : 3 (réponse) x 4 (diviseur) ;
- faites le calcul. Inscrivez ce résultat sous le dividende (valeur en haut à gauche). Dans notre exemple, on a donc : 3 x 4 = 12. On écrit 12 sous le 15 ;
- faites la soustraction des deux : 15 - 12 = 3. C'est votre reste.
-
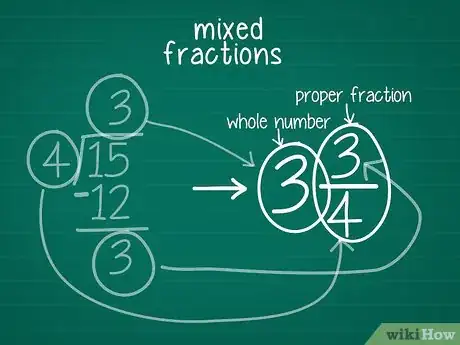
5Inscrivez votre réponse définitive. Il ne reste plus qu'à former le nombre mixte à l'aide de ces résultats. Un nombre mixte est composé d'une partie entière et d'une fraction irréductible. La division faite, vous avez tout ce qui est nécessaire à l'établissement du nombre mixte [5] .
- La partie entière sera le quotient (résultat de la division). Dans notre cas, c'est 3 (15 ÷ 4).
- Le numérateur de la partie fractionnaire est le reste. Dans notre cas, c'est aussi 3 (15-12).
- Quant au dénominateur, c'est le même que celui de la fraction de départ. Dans notre cas, c'est 4 (15/4).
- La réponse finale est donc : 33/4.
Publicité
Méthode 2
Méthode 2 sur 2:Sans diviser
-
1Inscrivez la fraction. Pour rappel, une fraction impropre est une fraction dont le chiffre du haut est supérieur à celui du bas, à l'image de 3 / 2 . En effet, 3 est supérieur à 2.
- Dans une fraction, le chiffre du haut est appelé numérateur, celui du bas, dénominateur.
- Cette méthode est un peu longue. Si le numérateur est bien supérieur au dénominateur, vous aurez meilleur compte à utiliser la méthode précédente.
-
2Sachez que certaines fractions valent 1. Savez-vous que : 2 ÷ 2 = 1 ? Ou que : 4 ÷ 4 = 1 ? En effet, tout nombre divisé par lui-même donne 1. Il en va de même avec les fractions. C'est ainsi que 2/2 = 1, que 4/4 = 1, ou encore que 397/397 = 1.
-
3Décomposez la fraction en deux autres fractions. C'est ainsi qu'on obtiendra dans un premier temps un nombre entier qui sera la partie entière du nombre mixte. Voyons comment on peut s'y prendre :
- avec 3/2, le dénominateur (nombre du bas) est 2 ;
- la fraction 2/2 est facile à simplifier, dans la mesure où les deux valeurs sont identiques. Nous allons sortir cette fraction de la fraction de départ et voir ce qui reste ;
- inscrivez : 3/2 = 2/2 + x/2.
-
4Trouvez la partie fractionnaire du nombre mixte. Par quel nombre remplacer « x » ? Si vous ne savez pas additionner et soustraire des fractions, pas de panique ! Pour une addition, quand les dénominateurs (nombres du bas) sont identiques, faites comme s'ils n'existaient pas et faites tranquillement la somme des numérateurs. Nous allons vous détailler l'opération suivante : 3/2 = 2/2 + x/2.
- Concentrez-vous sur les numérateurs (valeurs du haut). On a : 3 = 2 + x. Quel nombre ajouté à 2 donne 3 ?
- La réponse est 1, puisque 3 = 2 + 1.
- Au moment d'écrire la réponse définitive, on récrit l'égalité avec les dénominateurs : 3/2 = 2/2 + 1/2.
-
5Simplifiez la fraction [6] . Notre fraction impropre peut donc s'écrire : 3/2 = 2/2 + 1/2. On sait que : 2/2 = 1, comme toute fraction ayant les mêmes dénominateur et numérateur. On simplifie donc en haut et en bas par 2, ce qui donne 1. On a notre chiffre mixte : 1 + 1/2. Problème résolu !
- Il ne reste qu'une petite retouche à faire. Le signe « + » n'est plus nécessaire. La réponse définitive est donc : 11/2.
- Un nombre mixte est composé d'un nombre entier et d'une fraction irréductible [7] .
-
6Si la partie fractionnaire est impropre, recommencez le processus. Il arrive qu'on obtienne une partie fractionnaire impropre, dans laquelle on a un numérateur supérieur au dénominateur. Dans ce cas, il faut procéder comme on l'a déjà fait, c'est-à-dire trouver le nombre mixte qui en découle. N'oubliez pas, dans notre cas, d'ajouter le 1 de la partie entière. Soit l'exercice suivant : transformez 7/3 en nombre mixte.
- On décompose en deux fractions : 7/3 = 3/3 + x/3.
- On ne prend que les numérateurs : 7 = 3 + x.
- On trouve x : 7 = 3 + 4.
- On récrit : 7/3 = 3/3 + 4/3.
- On simplifie : 7/3 = 1 + 4/3.
- Cette dernière fraction est impropre. On va laisser de côté pour l'instant l'entier (1) pour réduire la fraction en un nouveau nombre mixte : 4/3 = 3/3 + x/3.
- On ne prend que les numérateurs : 4 = 3 + x.
- On trouve x : 4 = 3 + 1.
- On récrit : 4/3 = 3/3 + 1/3.
- On simplifie : 4/3 = 1 + 1/3.
- Cette dernière fraction est irréductible : l'exercice est résolu ! N'oubliez pas d'ajouter le 1 laissé de côté : 1 + (1 + 1/3) = 21/3.
Publicité
Références
- ↑ https://www.mathsisfun.com/improper-fractions.html
- ↑ http://www.mathgoodies.com/lessons/fractions/fractions_to_mixed.html
- ↑ https://www.mathgoodies.com/lessons/fractions/fractions_to_mixed
- ↑ http://www.aaamath.com/div41_x3.htm
- ↑ https://www.mathsisfun.com/mixed-fractions.html
- ↑ https://www.aaamath.com/fra66hx2.htm
- ↑ https://www.mathsisfun.com/mixed-fractions.html