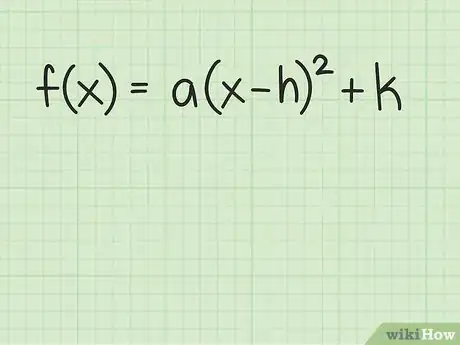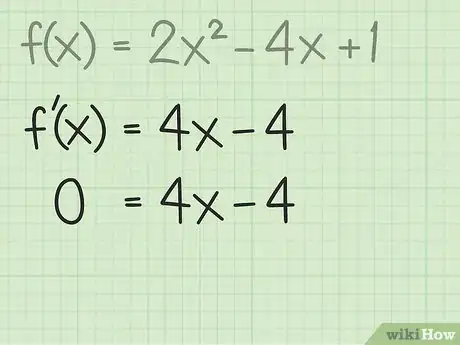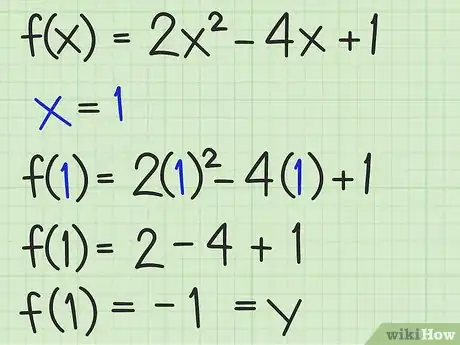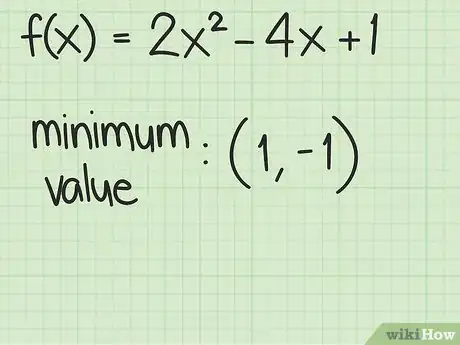Comment trouver facilement les valeurs maximale et minimale d’une fonction du second degré

Coécrit par Jake Adams

Dans l'étude des fonctions, au lycée par exemple, il arrive assez fréquemment que les professeurs de mathématiques demandent à leurs élèves de calculer le minimum ou le maximum d'une fonction du second degré. La détermination de cette valeur, qui est l'ordonnée du sommet, peut se faire à partir d'une fonction présentée sous sa forme développée ( $f(x)=ax^{2}+bx+c$ ) ou canonique ( $f(x)=a(x-h)^{2}+k$ ). Il est également possible de trouver les coordonnées de ce point en utilisant la dérivée, ce qui se fait obligatoirement quand vous devez faire un tableau de variation de la fonction.

Méthode 1

Méthode 1 sur 3:
Travailler à partir de la forme développée de la fonction

1
Présentez la fonction sous sa forme développée. Une fonction du second degré doit contenir au moins un terme $x^{2}$ $x^{2}$ , mais aucun exposant ne doit être supérieur à 2. Par contre, dans cette fonction, vous pouvez avoir des termes du premier degré ( $x$ $x$ ) et des constantes. Une fonction sous sa forme développée se présente ainsi : $f(x)=ax^{2}+bx+c$ $f(x)=ax^{2}+bx+c$ . Si cela s'avère nécessaire, vous serez peut-être amené à additionner certains termes et à les arranger pour obtenir une forme développée ^{[1]
X
Source de recherche}.
- Admettons qu'on vous donne la fonction suivante : $f(x)=3x+2x-x^{2}+3x^{2}+4$ $f(x)=3x+2x-x^{2}+3x^{2}+4$ . Regroupez les termes du second degré ( $x^{2}$ $x^{2}$ ) et ceux du premier ( $x$ $x$ ), et vous obtiendrez la fonction sous sa forme développée :
  - $f(x)=2x^{2}+5x+4$
2
Déterminez la concavité du graphe. Le graphe d'une fonction du second degré est une parabole, laquelle s'ouvre soit vers le haut soit vers le bas. Si $a$ $a$ , le coefficient du terme $x^{2}$ $x^{2}$ , est positif, vous aurez une parabole qui s'ouvre vers le haut. S'il est négatif, alors votre parabole s'ouvrira vers le bas. Prenons trois fonctions différentes ^{[2]
X
Source de recherche}.
- Dans l'équation $f(x)=2x^{2}+4x-6$ , $a=2$ (positif) : la parabole s'ouvre donc vers le haut.
- Dans l'équation $f(x)=-3x^{2}+2x+8$ , $a=-3$ (négatif) : la parabole s'ouvre cette fois vers le bas.
- Dans l'équation $f(x)=x^{2}+6$ , $a=1$ (positif) : la parabole s'ouvre vers le haut.
- Si la parabole s'ouvre vers le haut, vous pourrez déterminer la valeur minimale. Si la parabole s'ouvre vers le bas, c'est une valeur maximale que vous pourrez chercher.
3
Calculez -b/2a. En calculant $-{\frac {b}{2a}}$ $-{\frac {b}{2a}}$ , vous trouverez l'abscisse ( $x$ $x$ ) du sommet de la parabole. Pour cela, il faut que votre fonction sous présentée sous sa forme développée $ax^{2}+bx+c$ $ax^{2}+bx+c$ . Vous pourrez alors vous servir des coefficients de $x$ $x$ (b) et de $x^{2}$ $x^{2}$ (a) pour calculer $-{\frac {b}{2a}}$ $-{\frac {b}{2a}}$ .
- Pour l'équation $f(x)=x^{2}+10x-1$ $f(x)=x^{2}+10x-1$ , $a=1$ $a=1$ et $b=10$ $b=10$ . Le calcul de l'abscisse ( $x$ $x$ ) du sommet se fait ainsi :
  - $x=-{\frac {b}{2a}}$
  - $x=-{\frac {10}{(2)(1)}}$
  - $x=-{\frac {10}{2}}$
  - $x=-5$
- Pour mieux comprendre, prenons une seconde fonction $f(x)=-3x^{2}+6x-4$ $f(x)=-3x^{2}+6x-4$ . Dans cet exemple, $a=-3$ $a=-3$ et $b=6$ $b=6$ . L'abscisse du sommet se calcule comme suit :
  - $x=-{\frac {b}{2a}}$
  - $x=-{\frac {6}{(2)(-3)}}$
  - $x=-{\frac {6}{-6}}$
  - $x=-(-1)$
  - $x=1$
4
Trouvez l'ordonnée du sommet. Maintenant que vous avez trouvé $x$ $x$ , il ne vous reste plus qu'à mettre cette valeur dans la fonction de départ et vous obtiendrez l'ordonnée du sommet ( $y$ $y$ ou $f(x)$ $f(x)$ ). Cette valeur est appelée la valeur maximale ou minimale (selon le sens d'ouverture de la parabole) que ne dépassera jamais la fonction.
- Pour la première équation ( $f(x)=x^{2}+10x-1$ $f(x)=x^{2}+10x-1$ ), vous avez trouvé que l'abscisse du sommet était $x=-5$ $x=-5$ . Remplacez $x$ $x$ par $-5$ $-5$ dans la fonction de départ pour trouver la valeur maximale :
  - $f(x)=x^{2}+10x-1$
  - $f(x)=(-5)^{2}+10(-5)-1$
  - $f(x)=25-50-1$
  - $f(x)=-26$
- Pour la seconde équation ( $f(x)=-3x^{2}+6x-4$ $f(x)=-3x^{2}+6x-4$ ), vous avez trouvé que l'abscisse du sommet était $x=1$ $x=1$ . Remplacez $x$ $x$ par $1$ $1$ dans la fonction de départ pour trouver la valeur maximale :
  - $f(x)=-3x^{2}+6x-4$
  - $f(x)=-3(1)^{2}+6(1)-4$
  - $f(x)=-3+6-4$
  - $f(x)=-1$
5
Présentez votre résultat. Relisez la question qui vous a été posée. Si l’on vous demande de donner les coordonnées du sommet, vous devrez donner les deux résultats, à savoir $x$ $x$ et $y$ $y$ (ou si vous préférez $f(x)$ $f(x)$ ). Si la question portait juste sur le minimum ou le maximum de la fonction, ne donnez comme réponse que la valeur de $y$ $y$ (ou $f(x)$ $f(x)$ ). Faites attention au signe du coefficient $a$ $a$ pour savoir s’il s'agit d'un maximum ou d'un minimum.
- Pour la première équation ( $f(x)=x^{2}+10x-1$ ), vous remarquez que $a$ est positif, votre réponse sera donc la valeur minimale de la fonction. Le sommet est le point de coordonnées $(-5,-26)$ et la valeur minimale est $-26$ .
- Pour la seconde équation ( $f(x)=-3x^{2}+6x-4$ ), vous remarquez que $a$ est négatif, votre réponse sera donc la valeur maximale de la fonction. Le sommet est le point de coordonnées $(1,-1)$ et la valeur maximale est $-1$ .
Publicité

Méthode 2

Méthode 2 sur 3:
Travailler à partir de la forme canonique de la fonction

1
Mettez la fonction du second degré sous forme canonique. Outre la forme développée, assez courante, il est possible de présenter une fonction du second degré sous une forme plus factorisée, appelée canonique ^{[3]
X
Source de recherche} :
- La fonction se présente alors de la façon suivante : $f(x)=a(x-h)^{2}+k$ .
- Si la fonction que vous avez à traiter se présente déjà sous cette forme, il vous suffit de repérer les variables $a$ , $h$ et $k$ . Par contre, si la fonction est sous sa forme développée ( $f(x)=ax^{2}+bx+c$ ), vous devez la récrire sous sa forme canonique en complétant le carré.
- Pour vous rafraichir la mémoire concernant cette mise en forme canonique, lisez cet article.
2
Déterminez la concavité du graphe. Comme avec une fonction sous forme développée, il faut savoir de quel côté s'ouvre la parabole, vers le haut ou le bas. Si le coefficient $a$ $a$ est positif, alors la parabole s'ouvre vers le haut. S'il est négatif, alors la parabole s'ouvre vers le bas. Prenons quelques exemples en guise d'illustration ^{[4]
X
Source de recherche} :
- pour l'équation $f(x)=2(x+1)^{2}-4$ , $a=2$ , lequel est positif : la parabole s'ouvre donc vers le haut,
- pour l'équation $f(x)=-3(x-2)^{2}+2$ , $a=-3$ , lequel est négatif : la parabole s'ouvre donc vers le bas,
- si la parabole s'ouvre vers le haut, vous devrez chercher sa valeur minimale. Si elle s'ouvre vers le bas, c'est alors une valeur maximale qu'il faudra trouver.
3
Identifiez la valeur minimale ou maximale. Quand la fonction est sous sa forme canonique, trouver le minimum ou le maximum est d'une simplicité extrême, puisqu'il s'agit de la constante $k$ $k$ . Dans les deux exemples donnés précédemment, les valeurs sont les suivantes :
- pour l'équation $f(x)=2(x+1)^{2}-4$ , $k=-4$ . C'est la valeur minimale de la fonction, puisque la parabole s'ouvre vers le haut,
- pour l'équation $f(x)=-3(x-2)^{2}+2$ , $k=2$ . C'est la valeur maximale de la fonction, puisque la parabole s'ouvre vers le bas.
4
Trouvez les coordonnées du sommet. Si l'on vous demande de déterminer les coordonnées du sommet (là où est le minimum ou le maximum), sachez que ce point a pour coordonnées littérales $(h,k)$ $(h,k)$ . Vous remarquerez que, dans la forme canonique, la variable $h$ $h$ , dans le terme $(x-h)$ $(x-h)$ , est précédée du signe « - ». Il vous faut donc prendre l'opposé.
- Pour l'équation $f(x)=2(x+1)^{2}-4$ , le terme entre parenthèses est (x + 1), qui peut aussi s'écrire (x-(-1)). Par similitude, vous pouvez en déduire que $h=-1$ . En conséquence, les coordonnées du sommet de la parabole associée sont $(-1,-4)$ .
- Pour l'équation $f(x)=-3(x-2)^{2}+2$ , le terme entre parenthèses est (x - 2). Donc, tout simplement, $h=2$ . Les coordonnées du sommet de la parabole associée sont donc $(2,2)$ .
Publicité

Méthode 3

Méthode 3 sur 3:
Utiliser le calcul analytique pour trouver le minimum ou le maximum

1
Utilisez la fonction dans sa forme développée. Pour pouvoir dériver correctement, vous devez partir d'une fonction du second degré dans sa forme développée, à savoir $f(x)=ax^{2}+bx+c$ $f(x)=ax^{2}+bx+c$ . Si cela s'avère nécessaire, vous serez peut-être amené à additionner certains termes et à les arranger pour obtenir une forme développée ^{[5]
X
Source de recherche}.
- Commençons avec une fonction simple : $f(x)=2x^{2}-4x+1$ .
2
Déterminez la dérivée première de la fonction. Dériver consiste à modifier, en même temps et d'une certaine façon, le coefficient et la puissance de chaque terme d'une fonction. Ainsi, la dérivée première de $f(x)=ax^{2}+bx+c$ $f(x)=ax^{2}+bx+c$ est : $f^{\prime }(x)=2ax+b$ $f^{{\prime }}(x)=2ax+b$ ^{[6]
X
Source de recherche}.
- Pour la fonction $f(x)=2x^{2}-4x+1$ $f(x)=2x^{2}-4x+1$ , la dérivée est la suivante :
  - $f^{\prime }(x)=4x-4$
3
Mettez la dérivée égale à 0. En fait, la dérivée première d'une fonction permet de connaitre la pente de la courbe en un point donné. Partant de là, le minimum ou le maximum d'une fonction se trouve à l'endroit où la pente est nulle (la courbe change de sens). C'est pourquoi vous devez mettre la dérivée égale à 0. Pour plus de clarté, reprenons l'exemple précédent ^{[7]
X
Source de recherche} :
- $f^{\prime }(x)=4x-4$
- $0=4x-4$
4
Trouvez $x$ . En respectant les règles d'algèbre, déterminez la valeur de $x$ $x$ dans l'équation où la dérivée est égale à 0. Cette valeur sera l'abscisse du sommet de la fonction, l'autre coordonnée (ordonnée) sera le maximum ou le minimum de la fonction ^{[8]
X
Source de recherche}.
- $4x-4=0$
- $4x=4$
- $x=1$
5
Remplacez $x$ dans la fonction de départ. C'est ainsi que vous trouverez le minimum ou le maximum de la fonction. En fait, vous devez chercher l'ordonnée ( $y$ $y$ ) du point d'abscisse $x$ $x$ . Remplacez $x$ $x$ par la valeur que vous avez trouvée dans la fonction de départ, puis faites les calculs pour trouver le minimum ou le maximum ^{[9]
X
Source de recherche}.
- Pour la fonction $f(x)=2x^{2}-4x+1$ $f(x)=2x^{2}-4x+1$ , au point d'abscisse $x=1$ $x=1$ :
  - $f(1)=2(1)^{2}-4(1)+1$
  - $f(1)=2-4+1$
  - $f(1)=-1$
6
Présentez vos résultats. Les deux résultats précédents forment les coordonnées du sommet de la parabole. Pour la fonction $f(x)=2x^{2}-4x+1$ , le graphe présente un sommet ayant pour coordonnées $(1,-1)$ . Le coefficient $a$ étant positif, la parabole s'ouvre vers le haut. L'ordonnée de ce point (y), à savoir $-1$ , est aussi la valeur minimale que la fonction ne pourra jamais dépasser ^{[10]
X
Source de recherche}.

Publicité

Conseils

L'équation de l'axe de symétrie d'une parabole est : $x=h$

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Comment trouver facilement les valeurs maximale et minimale d’une fonction du second degré

Étapes

Méthode 1

Méthode 1 sur 3:
Travailler à partir de la forme développée de la fonction

Méthode 2

Méthode 2 sur 3:
Travailler à partir de la forme canonique de la fonction

Méthode 3

Méthode 3 sur 3:
Utiliser le calcul analytique pour trouver le minimum ou le maximum

Conseils

wikiHows en relation

Références

À propos de ce wikiHow

Articles en relation

Abonnez-vous à la newsletter gratuite de wikiHow !

Comment trouver facilement les valeurs maximale et minimale d’une fonction du second degré

Étapes

Méthode 1 Méthode 1 sur 3:Travailler à partir de la forme développée de la fonction

Méthode 2 Méthode 2 sur 3:Travailler à partir de la forme canonique de la fonction

Méthode 3 Méthode 3 sur 3:Utiliser le calcul analytique pour trouver le minimum ou le maximum

Conseils

wikiHows en relation

Références

À propos de ce wikiHow

Articles en relation

Abonnez-vous à la newsletter gratuite de wikiHow !

Méthode 1

Méthode 1 sur 3:
Travailler à partir de la forme développée de la fonction

Méthode 2

Méthode 2 sur 3:
Travailler à partir de la forme canonique de la fonction

Méthode 3

Méthode 3 sur 3:
Utiliser le calcul analytique pour trouver le minimum ou le maximum