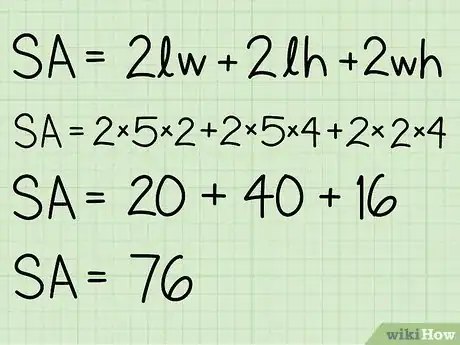Comment trouver l’aire d’une boite

Informations concernant l'auteur.e

Calculer l’aire d’une boite est un processus très simple, si vous connaissez les mesures de chaque côté. Une fois en possession de ces informations, il suffit d’utiliser l’équation correcte pour obtenir le résultat souhaité. Même en prenant de simples mesures, vous pouvez calculer la surface d’une boite de forme cylindrique.

Partie 1

Partie 1 sur 3:
Calculer l’aire d’une boite rectangulaire

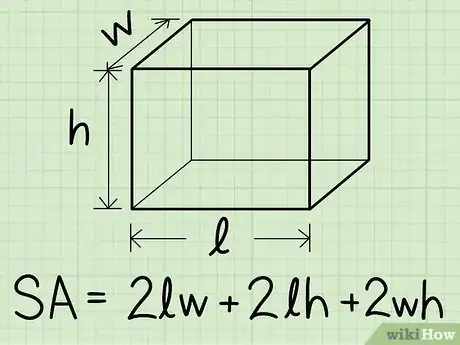
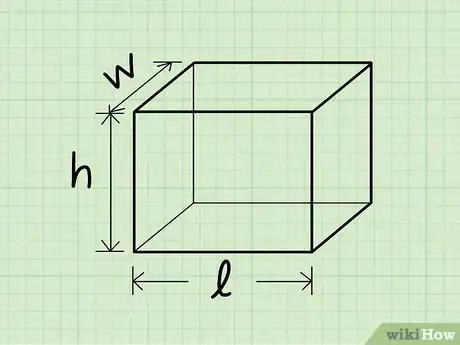
1
Calculez l’aire d’une boite rectangulaire. La surface d’un prisme droit à base rectangulaire est obtenue par la somme de l’aire de toutes les faces qui le composent. Si vous savez comment trouver l’aire d’un rectangle, qui revient tout simplement à multiplier la longueur par la largeur, vous pouvez trouver la solution de votre problème en additionnant l’aire de chaque côté. Cependant, il existe également une formule qui simplifie tout le processus de calcul lorsque vous connaissez les dimensions de la boite : $Aire=2Ll+2LH+2lH$ .
- L est la longueur de la boite, ou le côté le plus long.
- H est la hauteur.
- l est la largeur de la boite.
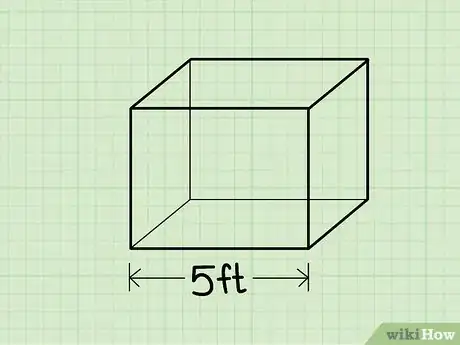
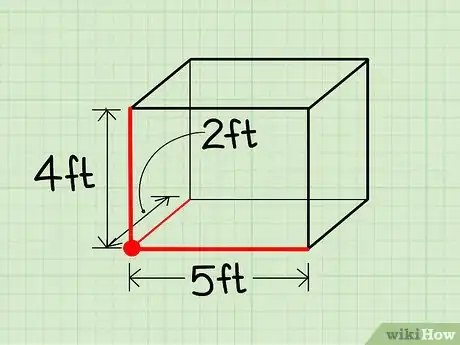
2
Mesurez la longueur de la boite. Il s’agit du côté le plus long. Il doit y avoir en tout 4 lignes identiques de même longueur. Posez par terre la boite sur son côté le plus long pour prendre plus facilement les mesures.
- Dans notre exemple, nous allons supposer que la longueur est de 5 cm.
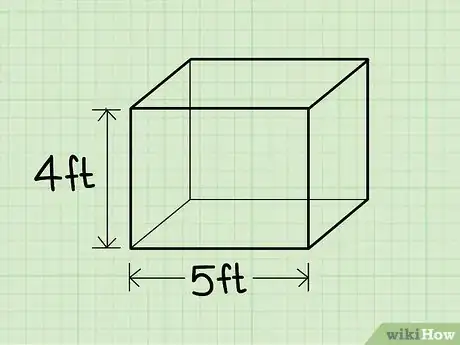
3
Mesurez la hauteur de la boite. C’est la distance entre le bord inférieur et le bord supérieur de la boite. Assurez-vous de ne pas mesurer une fois encore la longueur.
- Supposons que la hauteur est de 4 cm.
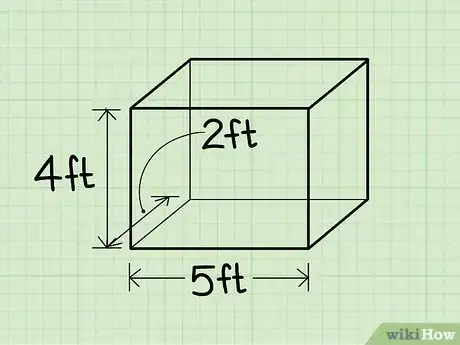
4
Mesurez la largeur de la boite. C’est le côté directement perpendiculaire à la longueur. Ne faites pas l’erreur de mesurer encore la hauteur.
- Dans notre exemple, nous supposons que la largeur de notre boite est égale à 2 cm.
5
Ne faites pas l’erreur de mesurer un même côté deux fois. Le moyen le plus simple pour éviter cela est de vous assurer que les trois dimensions (longueur, largeur et hauteur) convergent tous au même point. Choisissez un coin de la boite et mesurez les trois côtés qui partent de là. Ainsi, vous êtes sûr de prendre les bonnes mesures.
- Il convient de rappeler que les trois côtés peuvent également avoir les mêmes mesures (dans le cas d’un cube). Le plus important est de vous assurer de mesurer chacun des trois côtés, et ce, même s’il y a deux ou trois côtés qui sont identiques.
6
Remplacez les valeurs mesurées dans l’équation de départ. Une fois que vous connaissez les mesures de chaque côté, le reste du processus est très simple. Remplacez juste les valeurs et faites l’addition.
- $Aire=2Ll+2LH+2lH$
- $Aire=2(5)(2)+2(5)(4)+2(2)(4)$
- $Aire=20+40+16$
- $Aire=76$
7
Exprimez votre résultat en « unités au carré ». De cette façon, quand n’importe qui lira vos calculs, il sera en mesure de les interpréter correctement. En outre, utiliser la bonne unité de mesure représente une partie très importante de la solution à tous les problèmes en géométrie. Heureusement, c’est aussi une étape très simple. En fait, tout ce que vous devez faire est d’utiliser l’unité du problème. Dans notre exemple, les mesures ont été effectuées en centimètres (cm), donc notre résultat final sera exprimé en centimètres carrés (cm2).
- Quelle est l’aire totale d’une boite de 5 cm de longueur, 4 cm de hauteur et 2 cm de largeur ?
- Réponse : $76\,cm^{2}$
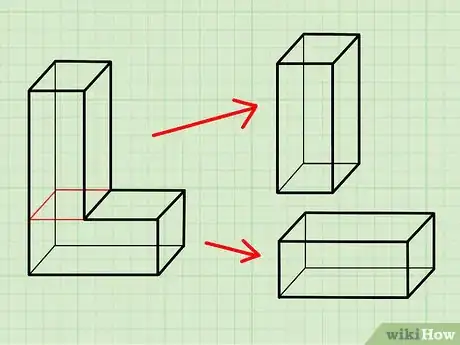
8
Calculez l’aire des boites ayant une forme complexe. Supposons que vous avez une boite en forme de « L ». Au lieu d’essayer de résoudre le problème directement, imaginez que cette boite est composée de deux éléments distincts, dont un constitue la base de la lettre « L » et l’autre représente la partie verticale (comme sur la photo ci-dessus). Calculez la superficie de chacun d’eux, puis faites la somme pour obtenir la surface totale ^{[1]
X
Source de recherche}. Par exemple, pour une boite sous forme de « U », les mesures peuvent être les suivantes.
- Supposons que la partie inférieure a une superficie de 12 centimètres carrés.
- Supposons que les deux bords verticaux ont chacune une superficie de 15 centimètres carrés.
- Dans ce cas, l’aire totale est égale à 42 centimètres carrés, soit $12+15+15=42$ .
Publicité

Partie 2

Partie 2 sur 3:
Calculer l’aire d’une boite cylindrique (tube)

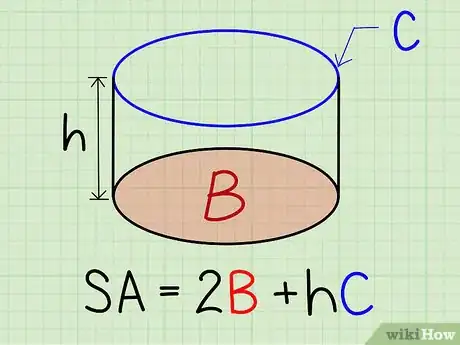
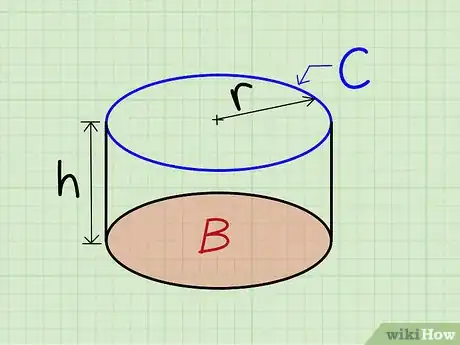
1
Calculez l’aire d’une boite cylindrique. Pour calculer l’aire d’un solide cylindrique, vous devez additionner l’aire des deux bases et le résultat obtenu par multiplication de la circonférence par la hauteur. Cette formule ne peut s’appliquer qu’aux cylindres droits, où la base forme un angle de 90 ° avec la section circulaire. La formule à utiliser est la suivante : $Aire=2B+HC$ Par exemple, quelle est l’aire d’un cylindre dont la base est égale à 3 centimètres carrés, la hauteur 5 cm et la circonférence 6 cm ? La réponse est égale à 36 centimètres carrés.
- B représente l’aire de la base.
- H est la hauteur du solide.
- C est la circonférence de la base ^{[2]
  X
  Source de recherche}.
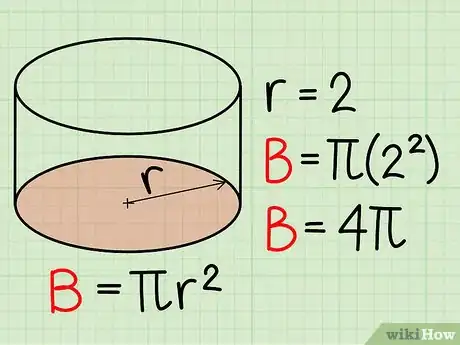
2
Calculez l’aire de la base de la boite. La base est l’extrémité circulaire sur laquelle repose le cylindre. Vous pouvez calculer l’aire de la base à l’aide de la formule suivante : Aire = π*r² r est le rayon du cercle. π est une constante géométrique dont la valeur est généralement arrondie à 3,14. Si vous n’avez pas une calculatrice, vous pouvez également laisser la constante π dans le résultat final.
- Dans notre exemple, supposons que le rayon de la base du cylindre est égal à 2 cm. Quelle est l’aire de base ?
- π*(2)²
- B = 4 π
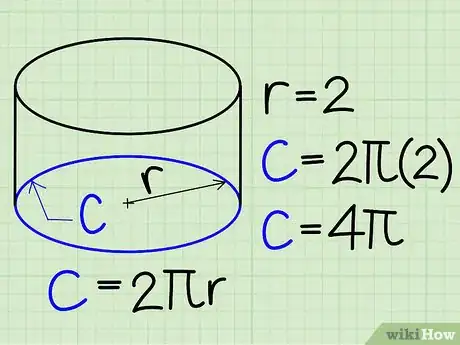
3
Calculez la circonférence de la base. En géométrie, la circonférence est la longueur du segment faisant le tour d'un cercle. Vous pouvez la calculer à l’aide de la formule suivante : Circonférence = 2*r*π En reprenant l’exemple précédent :
- 2*π*(2)
- C = 4π
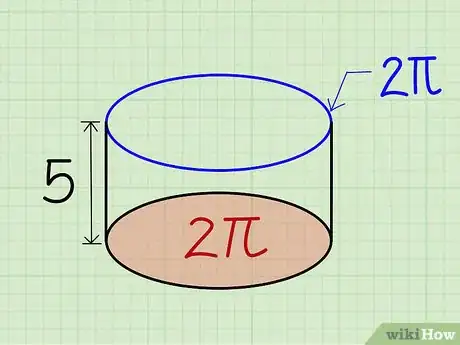
4
Trouvez la hauteur du cylindre. La hauteur d’un cylindre revient juste à déterminer la longueur du solide. C’est la ligne droite entre le centre et les deux bases.
- Dans notre exemple, supposons qu'un cylindre fait 5 cm de hauteur et 2 cm de rayon.
- $H=5$
5
Entrez les valeurs obtenues dans l’équation initiale. Après que vous ayez trouvé l’aire des deux bases, la circonférence et la hauteur, il suffit de remplacer ces valeurs avec leurs variables respectives dans la formule.
- Aire = 2B + HC
- Aire = 2(4π) + (5)(4π)
- Aire = 8 π + 20 π
- Aire = 28 π
6
Exprimez votre résultat en « unités au carré ». Tous les problèmes liés au calcul des aires impliquent l’utilisation d’unités carrées. Par exemple, si les données initiales sont fournies en millimètres, centimètres, mètres, l’unité de mesure utilisée pour exprimer l’aire doit toujours être au carré. Si aucune unité ne vous a été donnée, exprimez votre résultat en $m^{2}$ $m^{2}$ (mètre carré).
- Dans notre exemple, les mesures sont exprimées en centimètres. Donc le résultat final de nos calculs doit être exprimé comme suit : 28 π cm² ^{[3]
  X
  Source de recherche}.
Publicité

Partie 3

Partie 3 sur 3:
Faire des exercices

1
Résolvez des problèmes mettant en relief les rectangles. Pour afficher la réponse de ces exercices, sélectionnez l’espace blanc se trouvant juste à côté de la flèche.
- L = 10 cm, l = 3 cm, H = 2 cm, → 112 $cm^{2}$
- L = 6,2 cm, l = 2 cm, H = 5,4 cm, → 113,36 π $cm^{2}$
- Une boite rectangulaire de forme irrégulière a les mesures suivantes : la partie supérieure 5 x 3 x 2, la partie inférieure 6 x 2 x 2, → 118 π unités au carré.
2
Résolvez des problèmes mettant en relief les cylindres. Pour afficher la réponse de ces exercices, sélectionnez l’espace blanc se trouvant juste à côté de la flèche.
- Base = 3, Hauteur = 10, Circonférence = 1,5 → 21 unités au carré
- Base = 25 π, Hauteur = 3, Circonférence = 10 π →80 π unités au carré
- Rayon = 3, Hauteur = 3 → 36 π unités au carré
Publicité

Conseils

Si vous êtes en train de mesurer une véritable boite, vous pouvez essayer de prendre la mesure de différents bords, qui doivent d’ailleurs avoir la même longueur, puis utilisez la moyenne des différentes parties pour faire les calculs.