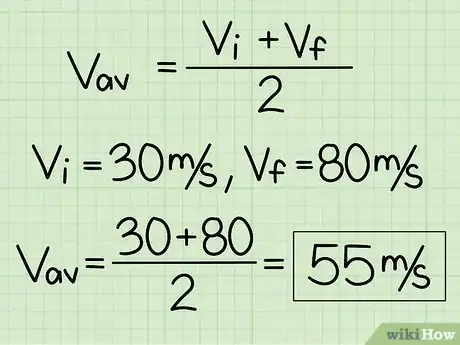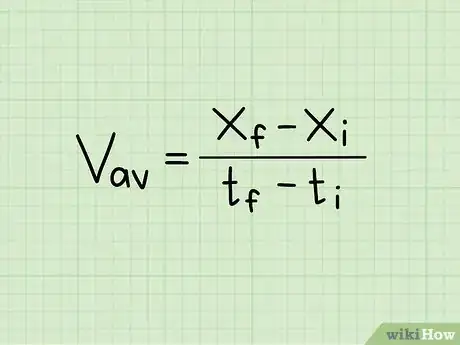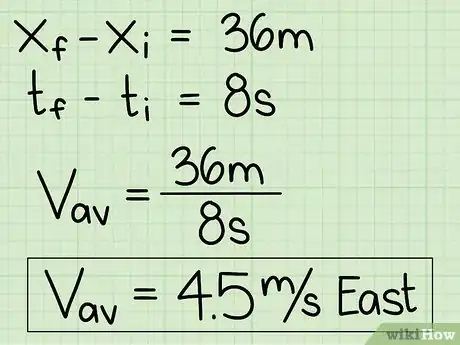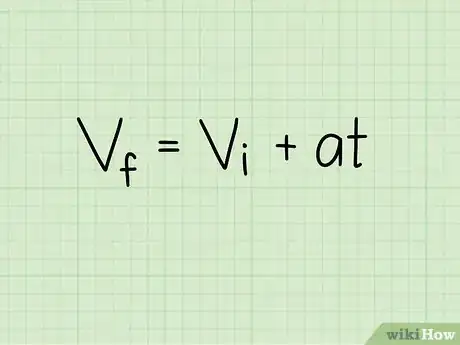Comment trouver la vitesse d’un corps en mouvement

En physique, la vélocité désigne le vecteur vitesse, c'est-à-dire la vitesse orientée d'un objet. Cependant, comme en mathématiques, on parle plutôt de vitesse, c'est-à-dire une variation de distance dans un intervalle de temps donné ^{[1]
X
Source de recherche}. On retrouve ce concept de vitesse dans de nombreux exercices et problèmes de physique. Il existe différentes formules de calcul de la vitesse, tout dépend en fait des données du problème que vous avez à résoudre.

Formules

Vitesse moyenne : $v_{m}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$ $v_{{m}}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$
- $x_{i}=$ position initiale $x_{f}=$ position finale
- $t_{i}=$ temps initial $t_{f}=$ temps final
Vitesse moyenne (avec accélération constante) : $v_{m}={\frac {v_{i}+v_{f}}{2}}$ $v_{{m}}={\frac {v_{i}+v_{f}}{2}}$
- $v_{i}=$ vitesse initiale $v_{f}=$ vitesse finale
Vitesse moyenne (avec accélération nulle) : $v_{m}={\frac {x}{t}}$
Vitesse finale : $v_{f}=v_{i}+at$ $v_{f}=v_{i}+at$
- a = accélération t = temps

Méthode 1

Méthode 1 sur 3:
Calculer une vitesse moyenne

1
Trouvez une vitesse moyenne à accélération constante. Si un objet a une accélération constante entre un point A et un point B, la formule de la vitesse moyenne est simple ^{[2]
X
Source de recherche} : $v_{m}={\frac {v_{i}+v_{f}}{2}}$ $v_{{m}}={\frac {v_{i}+v_{f}}{2}}$ . Dans cette formule, $v_{i}$ $v_{i}$ est la vitesse initiale, et $v_{f}$ $v_{f}$ , la vitesse finale. Il faut insister : cette formule ne peut s'appliquer que s'il y a une accélération constante.
- Prenons un exemple simple : soit un train qui passe de 30 m/s à 80 m/s en ayant une accélération constante sur la distance. Sa vitesse moyenne durant ce trajet sera de : ${\frac {30+80}{2}}=55m/s$ .
2
Posons la formule en fonction de la position et du temps. Il est possible de calculer la vitesse d'un objet à partir de la variation de sa position dans le temps. La formule est alors utilisable dans tous les cas de figure. Notez que, à moins que l'objet en question ne se déplace à vitesse constante, la réponse que vous aurez sera la vitesse moyenne de l'objet durant son parcours, et non la vitesse spécifique à un temps t.
- La formule est alors la suivante : $v_{m}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$ , dans laquelle on divise la différence entre la position finale et la position initiale, par la différence entre le temps final et le temps initial. Cette formule peut également s'écrire : $v_{m}$ = ^Δx / _Δt, dans laquelle on divise la variation de la distance par l'intervalle de temps.
3
Calculez la distance entre le point de départ et point d'arrivée. Quand on calcule une vitesse, les deux seules positions qui sont prises en compte sont celle de l'objet au départ et celle à l'arrivée. Ces deux éléments, plus la direction, nous donne ce qu'on appelle le déplacement ou la variation de position ^{[3]
X
Source de recherche}. Le trajet qui a pu être parcouru entre ces deux points n'entre pas en ligne de compte.
- Exemple n° 1 : une voiture se déplace en direction de l'est et part de la position x = 5 mètres. Après 8 secondes, la voiture est à x = 41 mètres. Quel a été le déplacement de la voiture ?
  - La voiture s'est déplacée de : 41 m - 5 m = 36 mètres vers l'est.
- Exemple n° 2 : un plongeur s'apprête à sauter d'un tremplin situé à 4 mètres de hauteur. Il monte d'abord d'un mètre (son élan) avant de retomber dans la piscine. Quel a été le déplacement du plongeur ?
  - Le plongeur s'est donc retrouvé 4 mètres plus bas que son point de départ, son déplacement a été de 4 mètres vers le bas, ou si vous préférez - 4 mètres (0 + 1 - 5 = - 4). Pourtant, le plongeur a parcouru six mètres (un mètre vers le haut, le même mètre vers le bas, puis les quatre mètres du tremplin vers le bas), mais ce qui nous importe ici c'est la différence entre le point de départ et le point d'arrivée, c'est-à-dire la hauteur du tremplin.
4
Calculez l'intervalle de temps. Cela revient à trouver le temps mis par un objet en mouvement pour atteindre un certain point d'arrivée. Dans certains exercices, cet intervalle vous sera donné, dans d'autres, il faudra le calculer en soustrayant le temps d'arrivée du temps de départ.
- Exemple n° 1 : on avait une voiture qui mettait 8 secondes pour aller du point de départ au point d'arrivée, ce qui fait que l'intervalle de temps est de 8 secondes.
- Exemple n° 2 : si le plongeur sautait à t = 7 s et touchait l'eau à t = 8 s, alors le temps de déplacement est de : 8 s - 7 s = 1 s.
5
Divisez le déplacement par l'intervalle de temps. Pour trouver la vitesse d'un objet en mouvement, il suffit de diviser la variation de distance par l'intervalle de temps. Cette vitesse moyenne doit également préciser le sens de déplacement.
- Exemple n° 1 : la voiture a couvert 36 mètres en 8 secondes. $v_{m}={\frac {36m}{8s}}=$ 4,5 m/s vers l'est.
- Exemple n° 2 : le plongeur a effectué un déplacement de - 4 mètres en une seconde, ce qui donne : $v_{m}={\frac {-4m}{1s}}=$ - 4 m/s. Par convention, dans un repère orthonormé, une valeur négative signifie un déplacement soit vers le bas soit vers la gauche. Ici, vous pourriez aussi bien écrire « 4 m/s vers le bas ».
6
Sachez résoudre des exercices en deux dimensions. Dans vos exercices, les trajectoires ne seront pas toujours linéaires. Les objets pourront changer de direction à plusieurs reprises. En ce cas, il faut faire un croquis des différentes trajectoires, puis reliez le point de départ au point d'arrivée. À partir de là, il faut se servir de formules de géométrie pour trouver le déplacement.
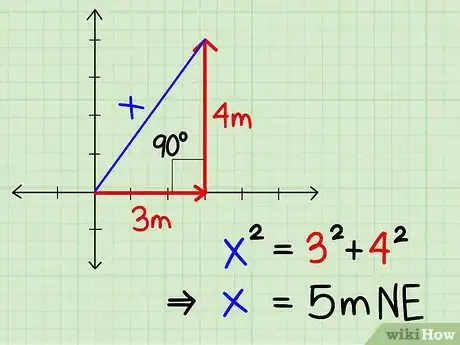
- Exemple n° 3 : un homme parcourt 3 mètres vers l'est, puis oblique à gauche à 90º pour parcourir 4 mètres vers le nord. De combien s'est-il déplacé ?
  - Faites un croquis, puis reliez par une ligne droite le point de départ et le point d'arrivée. Vous avez à présent devant vous un triangle rectangle dont l'hypoténuse représente le déplacement que l'on cherche. Pour trouver sa longueur, il faut se servir des propriétés du triangle rectangle. Dans notre cas, le déplacement a été de 5 mètres vers le nord-est.
  - Votre professeur de mathématiques (ou de physique) pourra vous demander de préciser la direction en donnant l'angle par rapport à l'horizontale. Pour cela, vous pourrez utiliser, un rapporteur ou faire du calcul vectoriel.
Publicité

Méthode 2

Méthode 2 sur 3:
Calculer une vitesse avec une accélération

1
Retenez la formule de la vitesse pour un objet qui accélère. L'accélération est la modification d'une vitesse. Si l'accélération est constante, la vitesse change régulièrement au fil du temps. Pour connaitre ce changement de vitesse, il suffit de multiplier l'accélération par la durée d'accélération. Pour avoir la vitesse finale d'un objet déjà en mouvement, on ajoute sa vitesse initiale.
- $v_{f}=v_{i}+at$ ou « vitesse finale = vitesse initiale + (accélération x temps) ».
- La vitesse initiale $v_{i}$ s'écrit également $v_{0}$ (vitesse à t = 0 s).
2
Multipliez l'accélération par l'intervalle de temps. Ce calcul permet de voir comment augmente (ou diminue) la vitesse au fil du temps.
- Exemple : un bateau fait route vers le nord à une vitesse de 2 m/s, puis accélère, dans la même direction, à raison de 10 m/s². De combien sa vitesse s'est-elle accrue au bout de 5 secondes ?
  - a = 10 m/s²
  - t = 5 s
  - (a x t) = (10 m/s² x 5 s) = 50 m/s (accroissement de la vitesse)
3
Ajoutez la vitesse initiale. Si vous voulez la vitesse après accélération, ajoutez la vitesse initiale de l'objet, et vous aurez votre réponse.
- Exemple : dans l'exemple du bateau, à quelle vitesse croisera-t-il au bout des 5 secondes ?
  - $v_{f}=v_{i}+at$
  - $v_{i}=2m/s$
  - $at=50m/s$
  - $v_{f}=2m/s+50m/s=52m/s$
4
Précisez la direction du déplacement. Dans certains problèmes, le sens de déplacement a son importance : n'oubliez alors jamais de spécifier cette direction.
- Dans l'exemple précédent, le bateau allait vers le nord et n'a pas changé de cap, si bien que sa vitesse finale est de 52 m/s vers le nord.
5
Résolvez des problèmes dérivés. À partir du moment où vous savez calculer une vitesse instantanée en un point quelconque grâce à l'accélération et la vitesse initiale, vous êtes capable, moyennant une transformation de la formule, de trouver une vitesse en n'importe quel point du parcours d'un objet. Vous pouvez, par exemple, calculer une vitesse initiale.
- Exercice : un train a accéléré pendant 4 secondes à 7 m/s², et a fini par avoir une vitesse de croisière de 35 m/s. Quelle était sa vitesse initiale ?
  - $v_{f}=v_{i}+at$
    $35m/s=v_{i}+(7m/s^{2})(4s)$
    $35m/s=v_{i}+28m/s$
    $v_{i}=35m/s-28m/s=7m/s$
Publicité

Méthode 3

Méthode 3 sur 3:
Calculer une vitesse de rotation

1
Apprenez la formule de la vitesse de rotation. C'est la vitesse qu'un objet doit avoir pour maintenir son orbite autour d'un autre objet (par exemple, une planète autour de son soleil) ou plus généralement, toute masse en gravitation ^{[4]
X
Source de recherche}.
- La vitesse de rotation d'un objet se calcule en divisant la circonférence parcourue (ou révolution) par le temps mis.
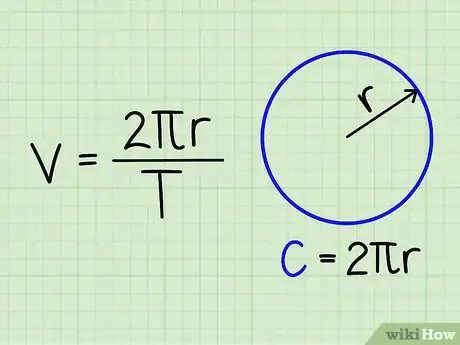
- Autrement dit, la formule est la suivante :
  - v = ^(2πr) / _t
- Le produit 2πr permet de calculer la circonférence d'une orbite circulaire.
- r est le rayon.
- t est l'intervalle de temps.
2
Multipliez le rayon (r) par 2π. La première étape consiste donc à calculer la circonférence. Il suffit pour cela de multiplier le rayon par 2π. Si vous faites les calculs à la main, prenez 3,14 comme valeur arrondie de π.
- Exemple : trouvez la vitesse de rotation d'un objet décrivant une trajectoire (T) circulaire de 8 mètres de rayon en 45 secondes.
  - r = 8 m
  - t = 45 s
  - Circonférence = 2πr = ~ (2)(3,14)(8 m) = 50,24 m
3
Divisez ce résultat par le temps de parcours. Afin d'obtenir la vitesse de rotation de l'objet en question, vous devez diviser la circonférence par le temps de parcours mis par l'objet.
- Exemple : v = ^(2πr) / _T = ^{50,24 m} / _{45 s} = 1,12 m/s
  - La vitesse de rotation de l'objet est de 1,12 m/s.
Publicité

Conseils

Le mètre par seconde (m/s) est l'unité de vitesse utilisée par les scientifiques ^{[5]
X
Source de recherche}. Si vous voulez que vos calculs soient exacts, vos distances doivent être en mètres (m), les temps en secondes (s) et l'accélération en mètres par seconde au carrée (m/s²).