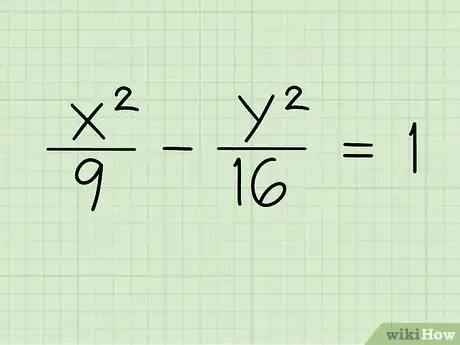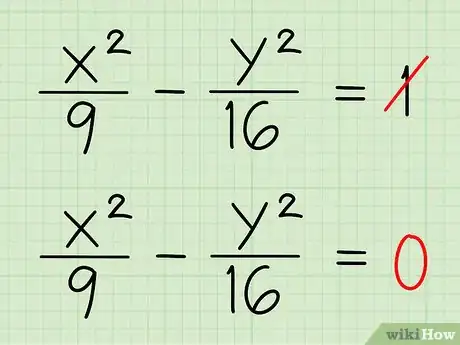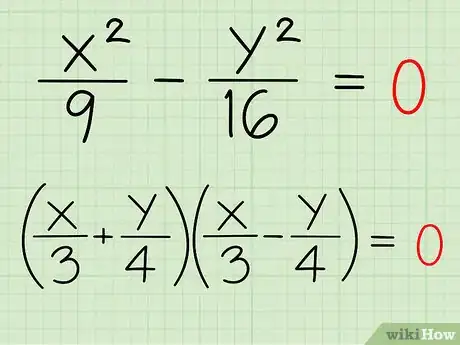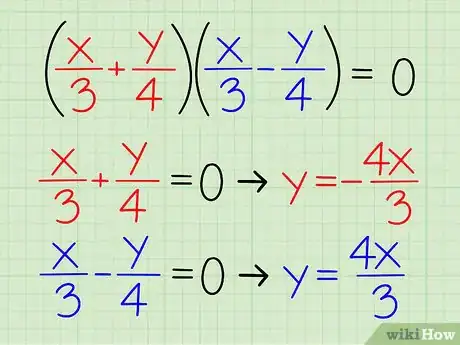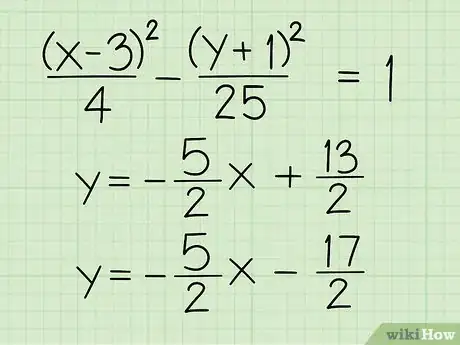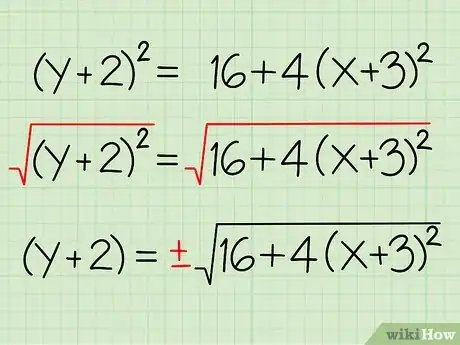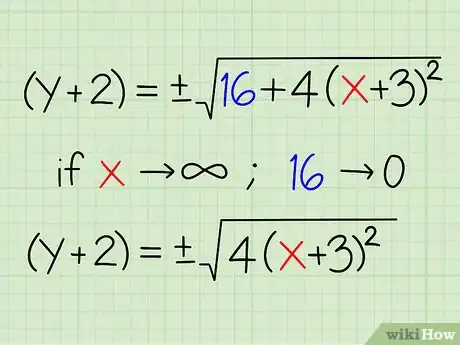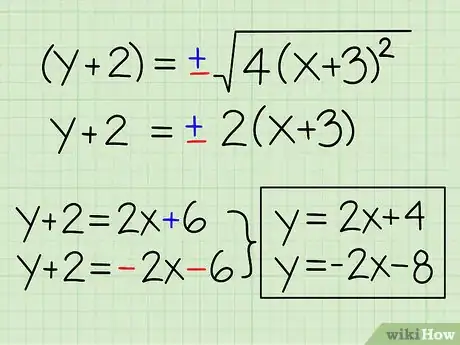Comment trouver les équations des asymptotes d'une hyperbole

Informations concernant l'auteur.e

Les lignes asymptotes d'une hyperbole sont des droites qui passent obligatoirement par le centre de symétrie de l'hyperbole. Toute hyperbole a des asymptotes dont elle se rapprochera, mais avec lesquelles elle n'aura jamais de point d'intersection. Il existe deux façons de déterminer les équations de ces asymptotes. En les passant en revue toutes les deux, vous comprendrez mieux ce qu'est une asymptote.

Méthode 1

Méthode 1 sur 2:
Trouver les équations des asymptotes en factorisant

1
Inscrivez l'équation de l'hyperbole sous sa forme standard. Nous prendrons comme exemple une hyperbole simple dont le centre est le point origine (0,0). Toutes les hyperboles de ce type ont une équation du genre ^x²/_a² - ^y²/_b² = 1 pour les hyperboles qui se développent horizontalement, ou ^y²/_b² - ^x²/_a² = 1 pour celles qui se développent verticalement ^{[1]
X
Source de recherche}. Dans cette équation, x et y sont des variables, tandis que a et b sont des constantes (en fait, des nombres réels).
- Exemple 1 : ^x²/₉ - ^y²/₁₆ = 1
- Les positions de a et b dans l'équation varient selon les manuels ou les professeurs ^{[2]
  X
  Source de recherche}. C'est pourquoi en abordant l'étude d'une hyperbole, vous devez reconnaitre à quel type elle appartient. N'apprenez pas les équations par cœur, sachez simplement reconnaitre leurs types.
2
Mettez cette équation égale à 0, et non à 1. Même s'il n'y parait pas, cette nouvelle équation contient en germe les équations des deux droites asymptotes. Quelques calculs permettront de les faire émerger ^{[3]
X
Source de recherche}.
- Exemple 1 : ^x²/₉ - ^y²/₁₆ = 0
3
Factorisez la nouvelle équation. Factorisez cette équation du second degré en un produit de deux facteurs. Si vous avez besoin de vous rafraichir un peu la mémoire sur la factorisation des équations du second degré, lisez cet article, sinon reprenons l'exemple en cours.
- Vous devez arriver à une équation de la forme : (__ ± __)(__ ± __) = 0.
- Le produit des deux premiers termes de chaque parenthèse doit donner ^x²/₉, c'est-à-dire que vous devez prendre la racine carrée, ce qui donne : (^x/₃ ± __)(^x/₃ ± __) = 0.
- De la même façon, extrayez la racine carrée de ^y²/₁₆ et placez le résultat dans les deux espaces laissés vacants : (^x/₃ ± ^y/₄)(^x/₃ ± ^y/₄) = 0.
- Il ne reste plus qu'à trouver les bons signes (« + » et « - »), de telle sorte que le produit des deux expressions donne l'équation de départ : (^x/₃ + ^y/₄)(^x/₃ - ^y/₄) = ^x²/₉ - ^y²/₁₆ = 0.
4
Trouvez les deux valeurs de y. Pour déterminer les équations des deux droites asymptotes, mettez chacun des facteurs égal à 0 et isolez, pour chacune des équations, y :
- Exemple 1 : comme (^x/₃ + ^y/₄)(^x/₃ - ^y/₄) = 0, nous savons que : ^x/₃ + ^y/₄ = 0 ou ^x/₃ - ^y/₄ = 0, ou les deux à la fois.
- Récrivez : ^x/₃ + ^y/₄ = 0 → ^y/₄ = - ^x/₃ → y = - ^4x/₃.
- Récrivez : ^x/₃ - ^y/₄ = 0 → - ^y/₄ = - ^x/₃ → y = ^4x/₃.
5
Essayez avec une hyperbole plus compliquée. Dans l'exemple précédent, le centre de symétrie était en (0,0), ce qui simplifiait le travail. Prenons le cas d'une hyperbole centrée au point (h,k), ce qui donne une équation du type : ^{(x - h)²}/_a² - ^{(y - k)²}/_b² = 1 ou du type : ^{(y - k)²}/_b² - ^{(x - h)²}/_a² = 1. En ce cas, utilisez cette même méthode de la factorisation, à la condition de garder ensemble, jusqu'à la dernière étape, les expressions (x - h) et (y - k).
- Exemple 2 : ^{(x - 3)²}/₄ - ^{(y + 1)²}/₂₅ = 1
- Mettez cette équation égale à 0 et factorisez, ce qui vous donne :
- (^{(x - 3)}/₂ + ^{(y + 1)}/₅)(^{(x - 3)}/₂ - ^{(y + 1)}/₅) = 0
- Pour déterminer les équations des deux droites asymptotes, mettez chacun des facteurs égal à 0 et isolez, pour chacune des équations, y :
- ^{(x - 3)}/₂ + ^{(y + 1)}/₅ = 0 → y = -⁵/₂x + ¹³/₂
- (^{(x - 3)}/₂ - ^{(y + 1)}/₅) = 0 → y = ⁵/₂x - ¹⁷/₂
Publicité

Méthode 2

Méthode 2 sur 2:
Trouver les équations des asymptotes en trouvant y

1
Inscrivez l'équation de votre hyperbole. Veillez à ce que le terme y² soit dans le membre de gauche. Cette méthode fonctionne, quelle que soit la forme de l'équation de l'hyperbole. Même si nous allons prendre un exemple en forme standard, vous allez comprendre la nature des asymptotes. Pour commencer, modifiez l'équation de façon à ce que le terme y² ou (y - k)² soit à dans le membre de gauche.
- Exemple 3 : ^{(y + 2)²}/₁₆ - ^{(x + 3)²}/₄ = 1
- Isolez les y à gauche, puis multipliez de chaque côté par 16, ce qui donne :
- (y + 2)² = 16(1 + ^{(x + 3)²}/₄)
- Simplifiez :
- (y + 2)² = 16 + 4(x + 3)²
2
Prenez la racine carrée de chacun des deux membres. Si vous pouvez extraire à gauche, laissez pour l'instant la racine carrée à droite. L'extraction d'une racine carrée débouche toujours sur deux solutions, égales en valeur absolue, mais de signes différents. Comme -2 x -2 = 2 x 2 = 4, vous pouvez en déduire que √4 est égal soit à 2 soit à -2. On utilise conventionnellement le signe ± pour signifier les deux solutions.
- √((y + 2)²) = √(16 + 4(x + 3)²)
- (y+2) = ± √(16 + 4(x + 3)²)
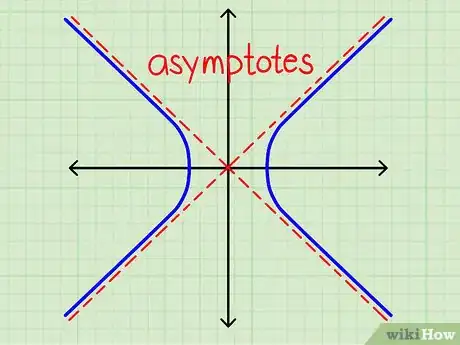
3
Comprenez bien ce qu'est une droite asymptote. Il est temps de le rappeler pour pouvoir poursuivre. Une droite asymptote d'une hyperbole est une droite que l'hyperbole tend à rejoindre au fur et à mesure que x s'accroit, mais jamais les deux droites ne se croiseront ni ne se toucheront, même à l'infini. Par contre, elles seront de plus en plus proches.
4
Rectifiez l'équation. Vous cherchez les équations des asymptotes et vous devez prendre en compte leurs limites à l'infini (valeurs élevées de x). En général, les constantes (ici 16) sont sans intérêt quand x a des valeurs tendant vers l'infini, ce qui fait qu'on les supprime. Si vous prenez x = 99 000 000 000, vous comprenez qu'ajouter 16 ne modifie quasiment rien.
- Avec cette équation (y+2) = ± √(16 + 4(x + 3)²), plus x tend vers l'infini, plus le « 16 » devient inopérant : vous pouvez le supprimer.
- Aux limites de l'infini, (y+2) est égal à peu de choses près à ± √(4(x + 3)²).
5
Établissez les équations des deux asymptotes. Après avoir éliminé la constante (non significative), vous pouvez faire les calculs pour simplifier. Isolez y pour les deux équations. Le symbole ± doit être dissocié en « + » et « - » pour obtenir les deux équations.
- y + 2 = ±√(4(x+3)²) = ±√4√((x+3)²)
- y + 2 = ±2(x+3)
- y + 2 = 2x + 6 et y + 2 = -2x - 6
- y = 2x + 4 et y = -2x - 8
Publicité

Conseils

Les équations d'une hyperbole et de ses asymptotes ont des constantes différentes.
Une hyperbole équilatère a une équation dans laquelle les constantes a et b sont égales.
Avec une hyperbole équilatère, il faut toujours démarrer de l'équation dans sa forme standard pour pouvoir trouver ses asymptotes.