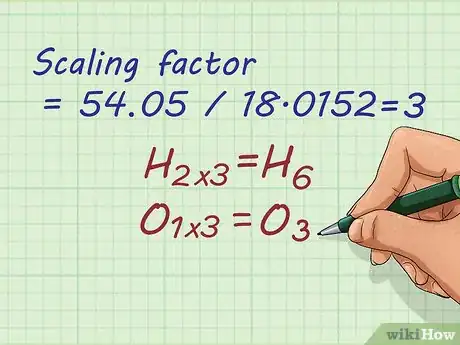X
Cet article a été coécrit par Mario Banuelos, PhD. Mario Banuelos est professeur adjoint de mathématiques à l'université d'État de Californie, à Fresno. Il a plus de huit ans d'expérience dans l'enseignement, et il est spécialisé dans la biologie mathématique, l'optimisation, les modèles statistiques pour l'évolution du génome et la science des données. Mario est titulaire d'une licence en mathématiques de l'université d'État de Californie, Fresno, et d'un doctorat en mathématiques appliquées de l'université de Californie, Merced. Mario a enseigné à la fois au lycée et à l'université.
Cet article a été consulté 12 814 fois.
Le coefficient de proportionnalité est un rapport, mais aussi une valeur numérique qui permet de passer d’une figure géométrique à une autre qui a la même forme et les mêmes angles, mais une aire et des côtés différents. Ce coefficient est souvent utilisé pour résoudre certains problèmes de géométrie. Il se calcule en rapportant les longueurs des deux côtés semblables sur les deux figures, mais il peut aussi servir à calculer une longueur manquante sur une des deux figures. Pour ces calculs, vous devrez savoir faire des divisions, des multiplications et simplifier des fractions.
Étapes
Méthode 1
Méthode 1 sur 4:Trouver le coefficient reliant deux figures proportionnelles
Méthode 1
-
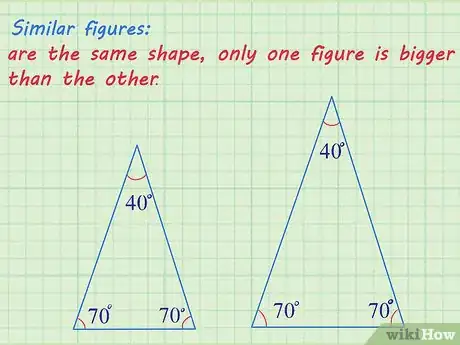
1Vérifiez bien que les deux figures sont proportionnelles. Les angles des deux figures doivent être strictement identiques. Cette mesure des angles est fondamentale. Les deux figures n’ont peut-être pas les mêmes aires, mais ces dernières sont aussi proportionnelles [1] .
- L’énoncé du problème vous apprendra, première hypothèse, que les deux figures (ou tous les côtés) sont proportionnelles. Seconde hypothèse : vous avez un dessin qui démontre à l’évidence que tous les angles, de figure à figure, sont égaux.
-
2Comparez deux côtés placés de la même façon sur les figures. Si la seconde figure n’a pas la même orientation que la première, débrouillez-vous pour que les deux figures soient facilement comparables. Là, de deux choses l’une : ou l’on vous donne les longueurs ou vous les mesurez avec une règle [2] . Si vous n’avez pas les longueurs de deux côtés semblables, il sera impossible d’établir le coefficient de proportionnalité qui les unit.
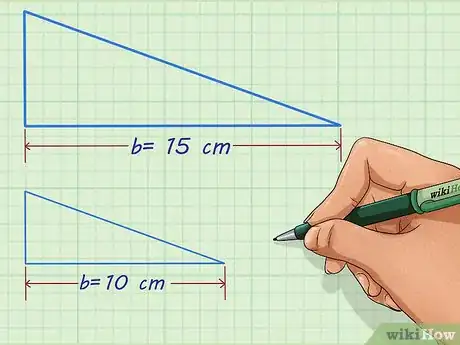
- Supposons que vous ayez un triangle dont la base mesure 15 cm et un autre triangle, proportionnel au premier, mais ayant seulement une base de 10 cm.
-
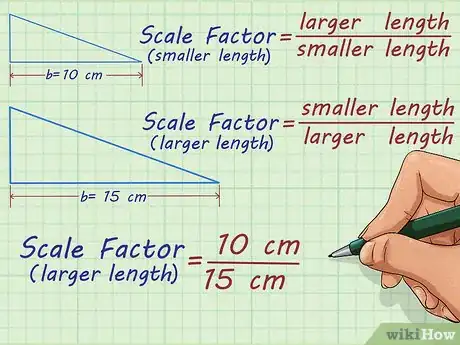
3Trouvez le rapport entre les deux dimensions. Quand vous comparez deux longueurs proportionnelles, ayez en tête qu’il y a en fait deux coefficients de proportionnalité, un dans le sens de l’agrandissement et son inverse dans le sens de la réduction. Si vous êtes dans le cas d’un agrandissement, de la petite à la grande figure, utilisez le coefficient de proportionnalité () suivant :
. Si vous êtes dans le cas d’une réduction, de la grande à la petite figure, utilisez le coefficient suivant :
[3] .- Ainsi, vous êtes dans le cas d’une réduction, pour passer d’un triangle ayant une base de 15 cm à son semblable, mais ayant une base de 10 cm, vous utiliserez le coefficient : .
L’application numérique donne le résultat suivant : .
- Ainsi, vous êtes dans le cas d’une réduction, pour passer d’un triangle ayant une base de 15 cm à son semblable, mais ayant une base de 10 cm, vous utiliserez le coefficient : .
-
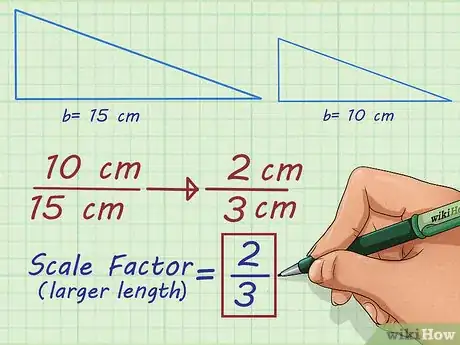
4Simplifiez la proportion. Si c’est possible, vous vous devez de simplifier ce coefficient à sa plus simple expression. Dans le cas d’une réduction, le coefficient de proportionnalité est une fraction propre, le numérateur est inférieur au dénominateur [4] . Dans le cas d’un agrandissement, votre rapport sera un nombre fractionnaire, une fraction impropre, voire une valeur de proportionnalité décimale supérieure à 1.
- Ainsi, le rapport est égal au rapport . En conséquence, le coefficient de proportionnalité de deux triangles proportionnels, dont l’un a une base de 15 cm et l’autre, de 10 cm, est de .
Publicité
Méthode 2
Méthode 2 sur 4:Trouver une figure dérivée du coefficient de proportionnalité
Méthode 2
-
1Récupérez les longueurs des côtés de la figure géométrique. Les longueurs de la figure doivent pouvoir être mesurées ou bien elles sont données dans le problème. En l’absence de ces données, vous ne pourrez trouver les dimensions d’une quelconque figure proportionnelle.
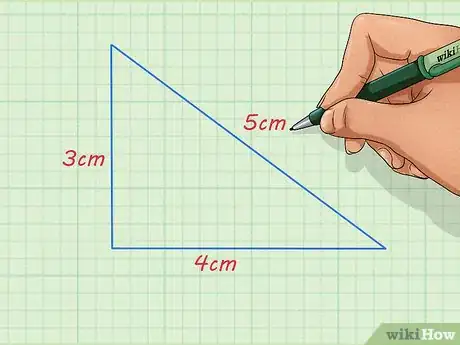
- Supposons que l’on vous donne, au départ, un triangle rectangle dont les côtés adjacents mesurent 3 et 4 cm, avec une hypoténuse de 5 cm de long.
-
2Qualifiez immédiatement le rapport entre les deux figures. Si le coefficient de proportionnalité est supérieur à 1 (entier ou décimal, fraction impropre), votre figure résultante sera plus grande que l’initiale. À l’inverse, s’il est inférieur à 1 (fraction propre), elle sera plus petite.
- Si, dans un exercice, le coefficient de proportionnalité est de 2, alors vous faites un agrandissement et votre figure finale sera plus grande que l’initiale.
-
3Multipliez une des longueurs de la figure par le coefficient. Dans ce type d’exercices, le coefficient de proportionnalité est toujours donné. Quand vous multipliez ces longueurs des côtés par le coefficient, vous obtenez une figure proportionnelle à celle de départ [5] .
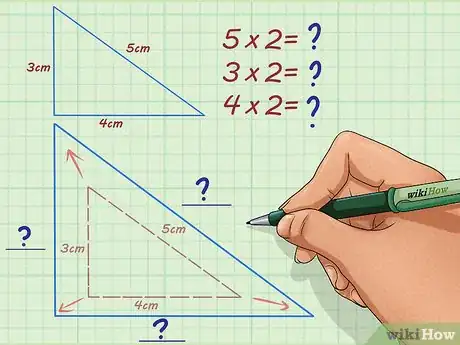
- Avec notre triangle rectangle ayant une hypoténuse de 5 cm de long et un coefficient de proportionnalité de 2, vous allez trouver que l’hypoténuse du triangle correspondant sera de 10 cm ().
-
4Trouvez les longueurs des autres côtés de la figure. Côté après côté, multipliez les autres longueurs par ce même coefficient de proportionnalité. Au terme de ces calculs, vous aurez toutes les dimensions de la figure proportionnelle.
- Notre triangle de départ à un côté (disons, la base) de 3 cm de long, ce qui, avec un coefficient de proportionnalité de 2, donne un côté de 6 cm
() pour la figure finale. Quant à l’autre côté du triangle (la hauteur), de 4 cm de longueur, il aura une longueur de 8 cm () dans le nouveau triangle.
Publicité - Notre triangle de départ à un côté (disons, la base) de 3 cm de long, ce qui, avec un coefficient de proportionnalité de 2, donne un côté de 6 cm
Méthode 3
Méthode 3 sur 4:Résoudre des problèmes de proportionnalité
Méthode 3
-
1Trouvez le coefficient de proportionnalité deux figures proportionnelles. Prenons un rectangle de 6 cm de largeur et un autre, proportionnel, de 54 cm de largeur.
- Établissez le coefficient de proportionnalité entre les deux figures. Si vous passez de la petite à la grande, le coefficient de proportionnalité (CP) est le suivant : . Si vous passez de la grande figure à la petite, le le coefficient de proportionnalité est inverse : .
- Simplifiez la proportion. La proportion est équivalente à
et le rapport équivaut à . Selon la proportionnalité envisagée, vous aurez un coefficient de proportionnalité de ou de .
-
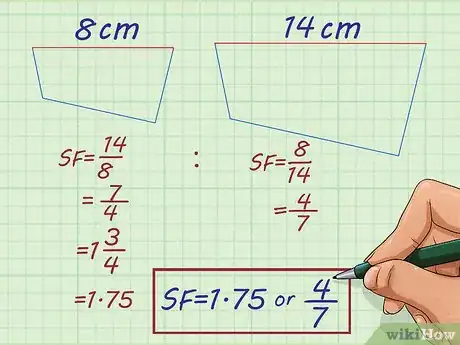
2Résolvez le problème suivant. Un polygone irrégulier fait, dans sa plus grande longueur, 14 cm. Un polygone irrégulier de même forme, mais plus petit, ne mesure que 8 cm. Quel est le coefficient de proportionnalité entre les deux ?
- Figure régulière ou non, à partir du moment où vous comparez deux côtés identiques, vous pouvez calculer le coefficient de proportionnalité qui unit les deux figures [6] .
- Les deux figures ont donc la même forme et les mêmes angles, vous pouvez calculer le coefficient de proportionnalité. Dans cet exemple précis, si vous passez du petit polygone au grand, le coefficient de proportionnalité se présente ainsi : . Si vous faites l’inverse, il se présente comme suit : .
- Simplifiez la proportion. La proportion est équivalente à , soit aussi , tandis que la proportion équivaut à . Selon le cas, vous indiquerez que les deux polygones irréguliers sont dans un rapport de ou de .
-
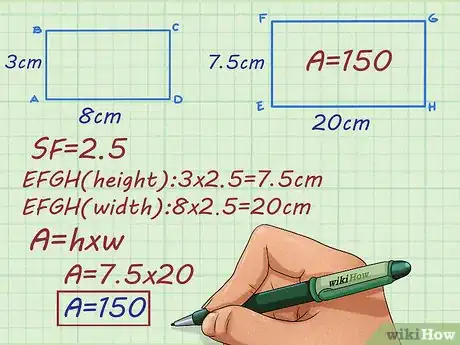
3Utilisez correctement le coefficient de proportionnalité. Résolvez l’exercice suivant : le rectangle ABCD fait 8 cm de long sur 3 de large. Le rectangle EFGH est plus grand, mais proportionnel. Sachant que le coefficient de proportionnalité entre les deux est de 2,5, quelle est l’aire du rectangle EFGH ?
- Multipliez la hauteur du rectangle ABCD par le coefficient de proportionnalité. La hauteur du rectangle EFGH est : .
- Multipliez la largeur du rectangle ABCD par le coefficient de proportionnalité. La largeur du rectangle EFGH est : .
- Multipliez la hauteur et la largeur du rectangle EFGH pour trouver son aire : . Réponse : le rectangle EFGH a une aire de 150 cm2.
Publicité
Méthode 4
Méthode 4 sur 4:Trouver un coefficient de proportionnalité en chimie
Méthode 4
-
1Divisez la masse molaire du composé par celle de la formule brute. On vous donne la formule brute d’un composé chimique et vous devez trouver sa formule moléculaire. Pour cela, vous allez pouvoir utiliser le coefficient de proportionnalité, lequel s’obtient en divisant la masse molaire du composé par celle de la formule brute.
- Supposons que vous ayez à trouver coefficient de proportionnalité d’un composé aqueux dont la masse molaire est de 54,05 g/mol.
- La masse molaire de l’eau (H20) est 18,0152 g/mol.
- Trouvez le coefficient en divisant la masse molaire du composé par la masse molaire de la formule brute.
- Le coefficient de proportionnalité est ici de : .
- Supposons que vous ayez à trouver coefficient de proportionnalité d’un composé aqueux dont la masse molaire est de 54,05 g/mol.
-
2Multipliez la formule brute par le coefficient de proportionnalité. Multipliez les indices de chacun des éléments de la formule brute par le coefficient que vous venez de trouver. Vous obtiendrez ainsi la formule moléculaire du composé chimique soumis à votre réflexion.
- Dans votre problème, vous devez multiplier tous les indices de la formule de l’eau (H20) par le coefficient de proportionnalité trouvé, soit 3.
- H20 x 3 = H6O3.
- Dans votre problème, vous devez multiplier tous les indices de la formule de l’eau (H20) par le coefficient de proportionnalité trouvé, soit 3.
-
3Rédigez correctement votre réponse. Après les calculs et la conversion, vous avez toutes vos réponses : coefficient de proportionnalité et formules moléculaires de l’eau et du composé. Rédigez-les dans un ordre logique et clairement afin d’avoir une bonne note.
- Ainsi, la proportion entre l’eau et le composé mystérieux est de 1 à 3 (coefficient de proportionnalité) et la formule moléculaire du composé est donc H6O3.
Publicité
Références
- ↑ http://www.mathsisfun.com/geometry/similar.html
- ↑ http://www.virtualnerd.com/pre-algebra/ratios-proportions/similar-figures-indirect-measurement/similar-figures/find-scale-factor-similar-figures
- ↑ http://www.bbc.co.uk/education/guides/zpwycdm/revision/2
- ↑ http://www.virtualnerd.com/pre-algebra/ratios-proportions/similar-figures-indirect-measurement/similar-figures/find-scale-factor-similar-figures
- ↑ http://www.virtualnerd.com/pre-algebra/ratios-proportions/missing-measurements-similar-figures-scale-factor.php
- ↑ http://www.vias.org/physics/bk1_03_02b.html
À propos de ce wikiHow
Mario Banuelos, PhD
Professeur assistant de mathématiques
Cet article a été coécrit par Mario Banuelos, PhD. Mario Banuelos est professeur adjoint de mathématiques à l'université d'État de Californie, à Fresno. Il a plus de huit ans d'expérience dans l'enseignement, et il est spécialisé dans la biologie mathématique, l'optimisation, les modèles statistiques pour l'évolution du génome et la science des données. Mario est titulaire d'une licence en mathématiques de l'université d'État de Californie, Fresno, et d'un doctorat en mathématiques appliquées de l'université de Californie, Merced. Mario a enseigné à la fois au lycée et à l'université. Cet article a été consulté 12 814 fois.
Catégories: Mathématiques
Publicité
