Cómo calcular Pi por tu cuenta usando círculos

Información del autor

¿Cómo se descubrió la constante matemática “pi”? ¿Alguien pudo hacerla? Bueno, con un poco de trabajo puedes descubrir la fuente del concepto, así como su valor aproximado. Está en todos los círculos y esferas, pero ¿dónde y cómo puedes encontrarla en la naturaleza de estas formas geométricas? Sigue leyendo para qué aprendas las instrucciones detalladas.

Método 1

Método 1 de 4:
Geometría básica de un círculo en el plano

1
Empieza por refrescar tus conocimientos de la geometría de un círculo en un plano. Sabemos mucho sobre los puntos, planos y espacios, ya que no están definidos en el estudio de la geometría, pero están descritos según su uso.
- ¿Qué es un círculo? La siguiente información tiene que formar parte de tu entendimiento (básico) de las cosas sobre los círculos, pero igual puedes aprender más en el camino.
- Equidistante - Es la forma corta de “de igual distancia”.
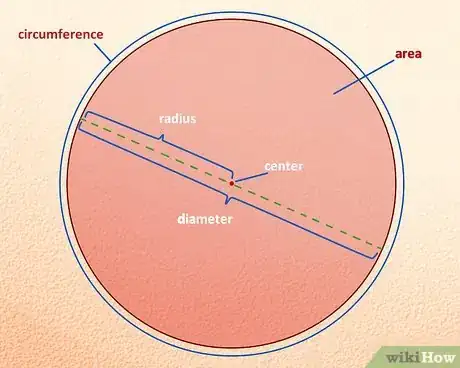
- Círculo - Todos los puntos equidistantes del centro (punto central).
- La siguiente información se relaciona pero NO es parte del círculo:
  - Centro - El punto equidistante de cualquier punto del círculo
  - Radio - El segmento (distancia) entre el punto central del círculo y cualquier punto de la circunferencia.
  - Diámetro - El segmento (distancia) entre dos puntos de la circunferencia, pasando por el punto central.
  - Segmento, área, sector y las formas incluidas o inscritas pero que no son parte del círculo.
  - Circunferencia - La distancia una vez alrededor del círculo.
    - Claro que esa palabra es larga y extraña así que piensa en la “distancia alrededor de una cerca circular”.

Método 2

Método 2 de 4:
Primero, crea una fórmula

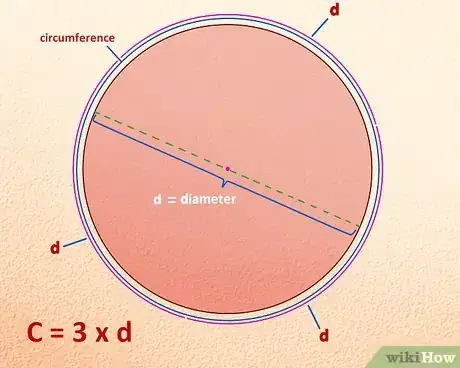
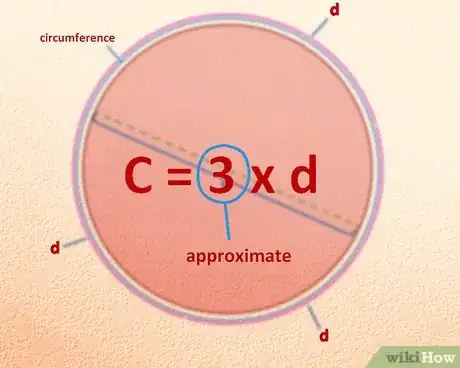
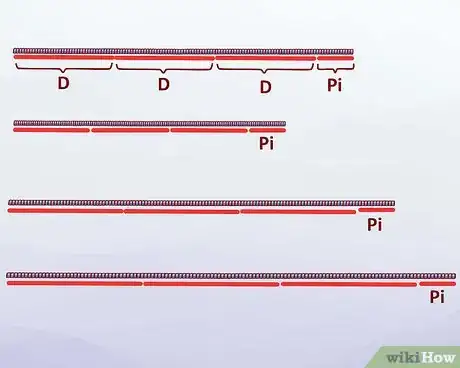
1
Descubre la fórmula de tu circunferencia. Puedes curvar el diámetro y colocarlo alrededor del círculo, de extremo a extremo, unas veces, lo cual significa que: tres diámeteros más una pequeña fracción del diámetro = Circunferencia. Llamemos a eso: C = 3 X d, aproximadamente. Listo (demasiado fácil). Es el mismo proceso que hubieras usado para descubrir la circunferencia hace 3000 o 4000 años. Ahora, limpiemos esa idea. En los tiempos antiguos, las matemáticas eran un estudio místico y tu “descubrimiento” era parte de la expresión de misterios matemáticos.
2
Debes interiorizar la idea de que pi vale alrededor de 3 y date cuenta de que puedes demostrar fácilmente que no es 3 exactamente. Ahora lo harás de forma más precisa.

Método 3

Método 3 de 4:
Calcula el valor exacto de Pi

1
Usa 4 contenedores o tapas circulares de distintos tamaños. También puedes usar una bola (esfera) pero es más difícil de medir.
2
Consigue una cuerda que no se estire ni sea ondulada. También necesitarás una regla o una vara para medir.
3
Haz un cuadro (o tabla) como el siguiente: Circunferencia | Diámetro | Cociente C / d = ?
1. __________|________|__________________
2. __________|________|__________________
3. __________|________|__________________
4. __________|________|__________________
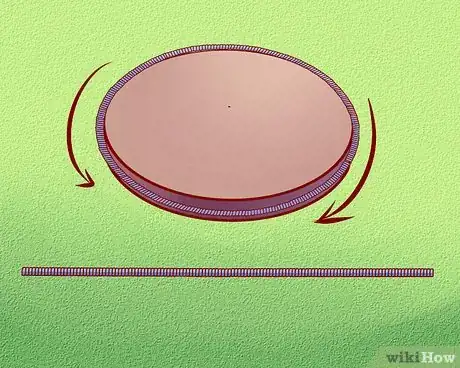
4
Envuelve cada uno de los círculos con la cuerda para medir la circunferencia de forma precisa. Marca la distancia de una vuelta al círculo en la cuerda. Esta es la circunferencia. Es simplemente el perímetro, sin embargo, al perímetro de un círculo normalmente se le conoce como circunferencia.
5
Estira la cuerda y mide la parte que marcaste en la cuerda. Esta es la distancia alrededor del círculo. Anota tus medidas de las circunferencias usando decimales. Asegura los extremos de la cuerda para estirarla y poder tomar medidas precisas. Así como la estiraste alrededor del círculo para medir la circunferencia, también debes estirarla para encontrar la distancia total a lo largo.
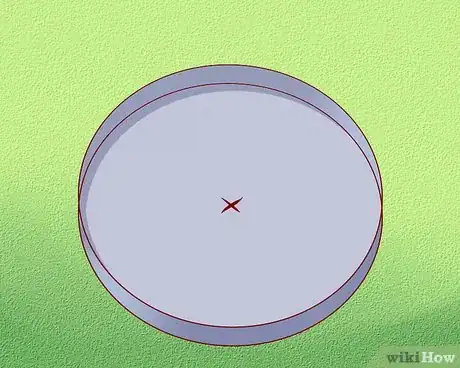
6
Voltea el contenedor para que puedas hallar y marcar el centro del círculo en la parte inferior. Así podrás medir el diámetro usando decimales (también conocidos como fracciones decimales).
7
Mide a lo largo del círculo pasando exactamente por el centro de cada uno de los artículos con una regla recta (también puedes usar un palito). Este es el diámetro.
- Nota: multiplicar el radio por 2 te da como resultado el diámetro, que también se puede expresar como 2r = d.
8
Divide cada circunferencia entre el diámetro del círculo. Los cuatro problemas de división de C / d = ____ te deben dar como resultado alrededor de 3 o 3,1 (o alrededor de 3,14 si tus mediciones fueron más precisas). Entonces, ¿qué es pi? Pi es un número. Es una razón. Relaciona el diámetro con la circunferencia. Claro, usar instrumentos más precisos para medir, como un compás, será de gran ayuda.
9
Promedia las cuatro respuestas del problema de división, sumando los cuatro cocientes y dividiéndolos entre 4. Eso debe darte un resultado más preciso (por ejemplo, si tus cuatro divisiones te dieron: 3,1 + 3,15 + 3,1 + 3,2 = ____/4 = ¿____? Ese resultado es 12,55 / 4 = 3,1375 y lo puedes redondear a 3,14).

Esa es la idea de pi. La cantidad de “diámetros” que hacen una circunferencia (todo el tiempo, es constante) Esa es la constante “pi”, la cantidad de diámetros.
- También, el radio entrará un poco más de 6 veces alrededor del círculo (2 veces pi) al igual que el diámetro entra un poco más de 3 veces. Eso implica que puedes expresar la fórmula de la circunferencia (C = 2 X 3,14 X r) simplemente como C = 3,14 X d. Si no lo entendiste, vuelve a repasarlo hasta que lo comprendas bien.
10
Finalmente, toma la cuerda con la que mediste el diámetro y úsala para medir y cortar la cuerda con la que mediste cada uno de los contenedores. El pedazo sobrante de cada uno de los cortes de la circunferencia debe ser de la misma longitud. Esta medida tendrá alrededor de 0,1415 veces la distancia del diámetro.

Método 4

Método 4 de 4:
Pista para los profesores

1
Ayuda a los estudiantes a que disfruten este ejercicio. Este puede ser uno de esos momentos en que se dan cuenta de la realidad y se sorprenden. Quizá digan “Me gustan las matemáticas mucho más de lo que pensé.” Debes hacer que parezca un experimento científico.
2
Si eres tutor o profesor, inventa una tarea “misteriosa” para tu clase.
3
Dales pistas. Enséñales o haz que te enseñen pero NO les digas cómo hacerlo. Deja que descubran las cosas. Si es muy fácil entonces el resultado será muy fácil para lo que tratas de enseñar. Entonces, hazlo de modo que los estudiantes puedan descubrirlo, como si fuera un misterio, y tengan una experiencia “Eureka”, no como si fuera un experimento más.
- No debes hacer que los alumnos lean un texto o miren una presentación como aquí, pero actúa con sutileza al principio: guíalos, ayúdalos y luego clarifica la idea, después que hayan presentados sus cuadros en cartulinas o paneles a su forma. Los estudiantes pueden presentar sus ideas en una pared y estar orgullosos de su razonamiento e ingenio al momento de trabajar.
4
Usa esto como un gran proyecto para la clase “arte, matemáticas, arte” (enseñanza cruzada). También puedes hacer que sea un proyecto para que los alumnos se lleven como tarea. Finalmente, después de aplicar este método, quizá te guste ser un gran profesor.

Consejos

Por si acaso: al arco de un círculo que tiene la misma longitud que el radio del círculo se le conoce como “rad”. Es una constante que se usa en trigonometría y cálculo.
Fórmula: Circunferencia = pi X diámetro.
- Resuelve para Pi de esta forma:

C = pi X d

C/d = (pi X d)/d

C/d = (pi)d/d

C/d = pi X 1 porque d/d = 1 lo cual nos da

C/d = pi

La razón C/d "define" la constante pi, sin importar el tamaño del círculo, en las ecuaciones geométricas, pero π también ocurre en áreas de las matemáticas que no involucran geometría directamente.

Puedes ver listados históricos en una tabla del valor de Pi y su cronología, donde se muestran desde ideas tempranas hasta cálculos modernos de millones de dígitos.^{[1]
X
Fuente de investigación}
Pi es la letra p, π en griego. El filósofo griego Arquímedes de Siracusa (287 – 212 B.C.) descubrió una aproximación de pi. Él obtuvo la siguiente inecuación:

223/71 < π < 22/7

Arquímedes sabía que π no era igual a 22/7, pero no mencionó haber descubierto un valor más exacto. Si estimamos Pi como un promedio de 223/71 y 22/7, entonces el resultado es 3,1418, un error de alrededor de 0,0002 (1% de error). ^{[2]
X
Fuente de investigación}
- Alrededor de 15 ciclos antes de Arquímedes, el Papiro Matemático Rhind de los egipcios, una página de un texto antiguo que explicaba problemas matemáticos, usó pi = 256 / 81. Eso es (16/9)², más o menos 3,16 (compáralo a 25/8 = 3.125).^{[3]
  X
  Fuente de investigación}
- Alrededor del año 250 antes de Cristo, Arquímedes también usó un valor de pi = 256/81 = suma de 3 + 1/9 + 1/27 + 1/81. Los egipcios también usaron el valor de pi = 3 + 1/13 + 1/17 + 1/160 = 3,1415 en el problema 50 del Papiro Matemático Rhind. ^{[4]
  X
  Fuente de investigación}

Cosas que necesitarás

5 contenedores circulares de distintos tamaños (pequeño, mediano, grande, más grande o inmenso)
Cuerda (que no sea ondulada)
Cinta adhesiva, tachuelas
Vara para medir o regla
Tabla o cuadro
Lápiz o lapicero
Calculadora (opcional, si la necesitas)