Cómo calcular el área y el perímetro

Coescrito por David Jia

Referencias

El perímetro es el borde externo completo de una figura. El área es el espacio que está dentro de ese borde externo.[1] El área y el perímetro son medidas extremadamente útiles que se pueden usar en proyectos domésticos, construcciones, proyectos de bricolaje y para la estimación de materiales que podrías necesitar.[2] Por ejemplo, el simple hecho de pintar una habitación requiere que sepas cuánta pintura vas a necesitar, en otras palabras, cuál es el área a cubrir con pintura. Se podría decir lo mismo si lo que necesitas es marcar un jardín, construir una valla o hacer muchas otras tareas en casa.[3] En estas situaciones, puedes usar el área y el perímetro para ahorrar tiempo y dinero a la hora de comprar los materiales.

Parte 1
Parte 1 de 2:
Calcular el perímetro

  1. Imagen titulada Find Area and Perimeter Step 1
    1
    Determina la forma de lo que vas a medir. El perímetro es el borde externo que rodea a una figura geométrica cerrada y cada forma necesita un enfoque diferente. Si la figura para la cual vas a calcular el perímetro no es una forma cerrada, entonces no puedes calcular su perímetro.
    • Si es la primera vez que vas a calcular el perímetro, intenta hacerlo con un rectángulo o un cuadrado. Para estas formas regulares, calcular el perímetro es más fácil.
  2. Imagen titulada Find Area and Perimeter Step 2
    2
    Dibuja un rectángulo en una hoja de papel. Usarás este rectángulo como una figura de práctica y calcularás su perímetro. Asegúrate de que los lados opuestos de tu rectángulo tengan la misma longitud.[4]
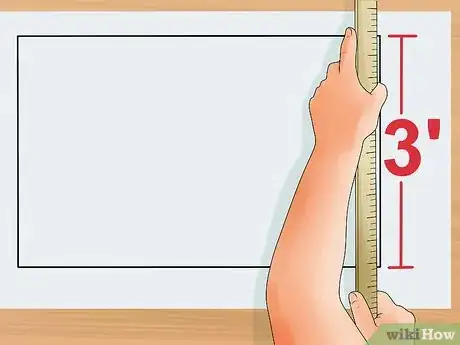
  3. Imagen titulada Find Area and Perimeter Step 3
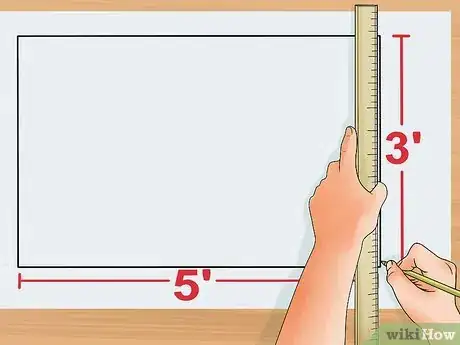
    3
    Calcula la longitud de uno de los lados del rectángulo. Puedes hacerlo con una regla, cinta métrica o inventando tu propio ejemplo. Escribe ese número cerca del lado que representa para no olvidar su longitud. Para hacer un ejemplo guiado, imagina que la longitud de uno de los lados del rectángulo es de 3 cm.
    • Si la forma es pequeña, puedes usar centímetros o pulgadas; si vas a calcular grandes perímetros, puedes usar metros, pies, millas o kilómetros, por ejemplo.
    • Debido a que los lados opuestos de un rectángulo son iguales, solo tienes que medir uno de cada par de lados opuestos.[5]
  4. Imagen titulada Find Area and Perimeter Step 4
    4
    Averigua cuál es el ancho de uno de los lados de tu rectángulo. Puedes hacerlo con una regla, cinta métrica o inventando tu propio ejemplo. Escribe el valor del ancho cerca del lado horizontal que representa en el rectángulo.
    • Continuando con el ejemplo guiado, imagina que además de una longitud de 3 cm, el ancho de tu rectángulo es de 5 cm.
  5. Imagen titulada Find Area and Perimeter Step 5
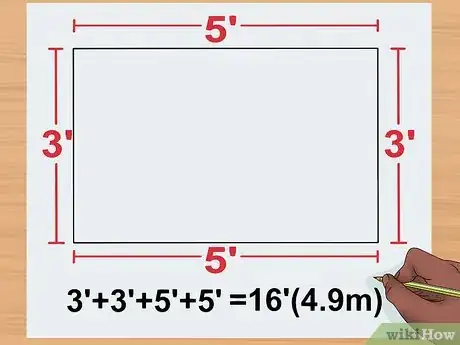
    5
    Anota las medidas correspondientes en los lados opuestos de tu rectángulo. Los rectángulos tienen cuatro lados, pero la longitud de los lados opuestos es la misma.[6] Esto también se cumple para el ancho del rectángulo. Agrega la longitud y el ancho que usaste en el ejemplo guiado (3 cm y 5 cm respectivamente) en los lados opuestos de tu rectángulo.
  6. Imagen titulada Find Area and Perimeter Step 6
    6
    Suma todos los lados. En una hoja de papel borrador o en el papel donde escribiste el ejemplo guiado, escribe: longitud + longitud + ancho + ancho.
    • De este modo, para el ejemplo guiado, deberás sumar 3 + 3 + 5 + 5 para obtener un perímetro de 16 cm.[7]
    • También puedes usar la fórmula 2(longitud + ancho) en los rectángulos, ya que los valores de longitud y ancho están duplicados. En el ejemplo anterior, podrías multiplicar 2 por 8 para obtener 16 cm.
  7. Imagen titulada Find Area and Perimeter Step 7
    7
    Ajusta este enfoque a otras formas diferentes. Desafortunadamente, necesitarás de distintas fórmulas para calcular el perímetro de distintas figuras. En ejemplos de la vida real, puedes medir el borde externo de cualquier figura geométrica para hallar la medida de su perímetro. Pero también puedes usar las siguientes fórmulas para calcular el perímetro de otras figuras comunes:
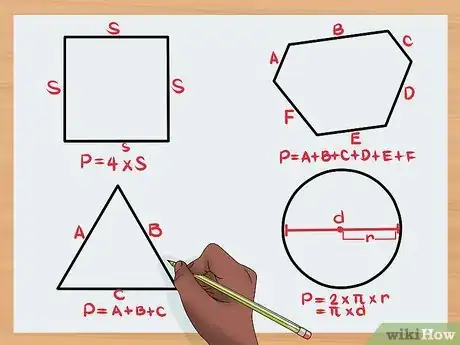
    • Cuadrado: longitud de cualquier lado x 4
    • Triángulo: lado 1 + lado 2 + lado 3
    • Polígono irregular: la suma de todos los lados
    • Círculo: 2 x π x radio O π x diámetro[8]
      • El símbolo π significa Pi (y se pronuncia como se lee). Si tienes una tecla π en tu calculadora, puedes usarla para ser más preciso a la hora de aplicar la fórmula. De lo contrario, puedes aproximar el valor de π a 3,14.[9]
      • El término "radio" se refiere a la distancia entre el centro del círculo y su borde externo (o perímetro), mientras que el "diámetro" se refiere a la longitud que hay entre dos puntos opuestos del perímetro del círculo atravesando el centro del mismo.[10] [11]
    Anuncio

Parte 2
Parte 2 de 2:
Calcular el área

  1. Imagen titulada Find Area and Perimeter Step 8
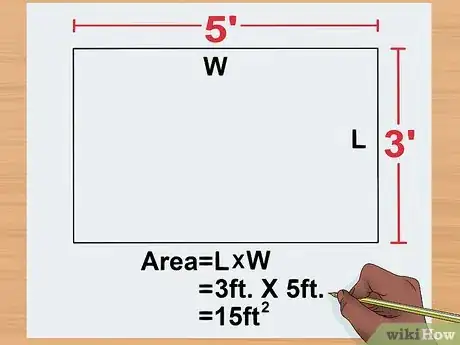
    1
    Determina las dimensiones de tu fórmula. Dibuja un rectángulo o utiliza el mismo rectángulo que usaste para calcular el perímetro. En este ejemplo guiado, se utilizará la altura y el ancho de tu rectángulo para calcular su área.
    • Puedes usar una regla, una cinta métrica o inventar tu propio ejemplo. Para los fines de este ejemplo guiado, la longitud y el ancho serán los mismos que se usaron en el ejemplo anterior para calcular el perímetro: 3 y 5 respectivamente.
  2. Imagen titulada Find Area and Perimeter Step 9
    2
    Comprende el verdadero significado del área. Encontrar el área que está dentro de un perímetro es como dividir ese espacio vacío dentro de tu forma en cuadrados individuales de 1 unidad por 1 unidad. El área puede ser más pequeña o más grande que el perímetro dependiendo de la figura.
    • Puedes dividir tu diagrama en segmentos de una unidad (expresada en centímetros, metros, kilómetros…) verticalmente y horizontalmente si quieres visualizar cómo ser verá la medida del área.
  3. Imagen titulada Find Area and Perimeter Step 10
    3
    Multiplica la longitud del rectángulo por su ancho. Para el ejemplo guiado, deberás multiplicar 3 por 5 para obtener un área de 15 cm cuadrados. La unidad de medida del área siempre se expresará en unidades al cuadrado (centímetros cuadrados, metros cuadrados, kilómetros cuadrados, etc.).
    • Puedes escribir la forma abreviada de "unidades cuadradas" o "unidades al cuadrado" de la siguiente forma:
      • metros2 o m2
      • centímetros2 o cm2
      • kilómetros2 o km2
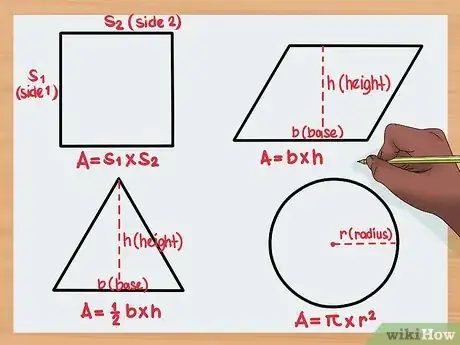
  4. Imagen titulada Find Area and Perimeter Step 11
    4
    Cambia la fórmula de acuerdo con la figura. Desafortunadamente, necesitarás de distintos enfoques para calcular el área de distintas figuras. Puedes usar las siguientes fórmulas para encontrar el área de algunas de las figuras más comunes:
    • Paralelogramo: base por altura
    • Cuadrado: lado 1 x lado 2
    • Triángulo: ½ de la base x altura
      • Algunos matemáticos utilizan la notación: A=½bh (donde b es la base y h es la altura)
    • Círculo: π x radio2
      • El término "radio" se refiere a la distancia entre el centro del círculo y su borde externo (o perímetro), y el 2 elevado (que se conoce como la notación para elevar un término "al cuadrado") indica que ese valor, al estar elevado al cuadrado, debe multiplicarse por sí mismo.[12] [13]
    Anuncio

Consejos

  • Las fórmulas tanto del área como del perímetro solo funcionan para aplicarlas en figuras (bidimensionales). Si necesitas calcular el "área" de un cuerpo tridimensional, que se conoce como volumen, necesitarás encontrar las fórmulas para calcular el volumen, que generalmente incluyen: conos, cubos, cilindros, prismas y pirámides.
Anuncio

Cosas que necesitarás

  • Papel
  • lápiz
  • calculadora (opcional)
  • cinta métrica (opcional)
  • regla (opcional)

wikiHows relacionados

calcular el diámetro de un círculo
Cómo
calcular el diámetro de un círculo
calcular un incremento en porcentaje
Cómo
calcular un incremento en porcentaje
calcular la variación porcentual
Cómo
calcular la variación porcentual
encontrar el valor de X
Cómo
encontrar el valor de X
medir milímetros
Cómo
medir milímetros
calcular una frecuencia
Cómo
calcular una frecuencia
calcular las probabilidades de sacarte la lotería
Cómo
calcular las probabilidades de sacarte la lotería
convertir de grados a radianes
Cómo
convertir de grados a radianes
calcular la varianza
Cómo
calcular la varianza
calcular la incertidumbre
Cómo
calcular la incertidumbre
convertir radianes a grados
Cómo
convertir radianes a grados
calcular la velocidad
Cómo
calcular la velocidad
calcular el porcentaje de error
Cómo
calcular el porcentaje de error
encontrar una raíz cuadrada sin una calculadora
Cómo
encontrar una raíz cuadrada sin una calculadora
Anuncio

Referencias

  1. ↑ http://www.diffen.com/difference/Area_vs_Perimeter
  2. ↑ https://sites.google.com/site/tracielawn/lessons/handyman-101-the-use-of-area-and-perimeter-in-the-real-world
  3. ↑ http://www.teach-nology.com/teachers/subject_matter/math/geometry/
  4. ↑ https://www.mathsisfun.com/definitions/rectangle.html
  5. ↑ http://www.mathopenref.com/rectangle.html
  6. ↑ http://www.mathopenref.com/rectangle.html
  7. ↑ https://www.khanacademy.org/math/geometry/basic-geometry/perimeter_area_tutorial/v/perimeter-and-area-basics
  8. ↑ http://perimeterofacircle.com/
  9. ↑ http://www.mathopenref.com/pi.html
  1. ↑ http://www.mathopenref.com/radius.html
  2. ↑ http://www.mathopenref.com/diameter.html
  3. ↑ http://www.mathopenref.com/radius.html
  4. ↑ https://www.mathsisfun.com/definitions/square-number.html

Acerca de este wikiHow

David Jia
Coescrito por:
David Jia
Tutor académico
Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math. Este artículo ha sido visto 1 008 628 veces.
Categorías: Matemáticas
Anuncio