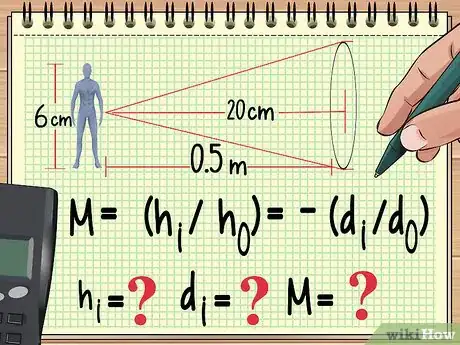Cómo calcular el aumento óptico

En la ciencia de la óptica, el aumento de un objeto, como una lente, constituye la proporción entre la altura de la imagen que se puede ver y la altura del objeto en sí que se aumenta. Por ejemplo, una lente que hace que un objeto pequeño parezca muy grande tiene un aumento alto, en tanto que una lente que hace que un objeto tenga un aspecto pequeño tiene un aumento bajo. Por lo general, el aumento de un objeto se obtiene mediante la ecuación M = (h_i/h_o) = -(d_i/d_o), en donde M = aumento, h_i = altura de la imagen, h_o = altura del objeto, y d_i y d_o = distancia de la imagen y del objeto.

Método 1

Método 1 de 2:
Encontrar el aumento de una sola lente

Nota: una lente convergente es más ancha en el centro que en los bordes (como una lupa). Una lente divergente es más ancha en los bordes que en el centro (como un tazón).^{[1]
X
Fuente de investigación} Encontrar el aumento es igual para ambas salvo por una excepción importante. Haz clic aquí para ir directamente a la excepción de las lentes divergentes.

1
Empieza por la ecuación y determina cuáles son las variables que conoces.^{[2]
X
Fuente de investigación} Como ocurre con muchos otros problemas de física, una buena forma de abordar los problemas de aumento es escribiendo primero la ecuación necesaria para encontrar la respuesta. A partir de aquí, puedes trabajar a la inversa para encontrar las partes de la ecuación que necesites.^{[3]
X
Fuente de investigación}
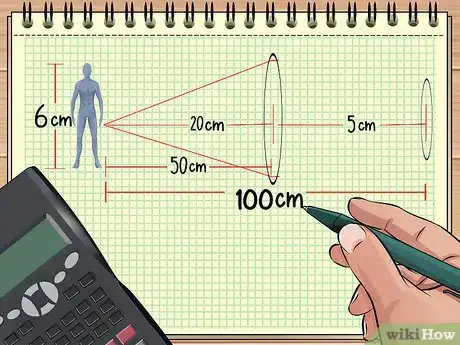
- Por ejemplo, imagina que se coloca una figura de acción de 6 cm de alto a medio metro de una lente convergente que tiene una distancia focal de 20 cm. Si lo que quieres es encontrar el aumento, el tamaño de la imagen y la distancia de la imagen, puedes empezar por escribir la ecuación de la siguiente forma:
  M = (h_i/h_o) = -(d_i/d_o)
- Ahora mismo, conoces h_o (la altura de la figura de acción) y d_o (la distancia de la figura a la lente). Asimismo, sabes la distancia focal de la lente, la cual no se encuentra en esta ecuación. Es necesario encontrar h_i, d_i y M.
2
Utiliza la ecuación de la lente para obtener d_i. En caso de que conozcas la distancia entre el objeto que vayas a aumentar y la lente, y la distancia focal de la lente, será fácil encontrar la distancia de la imagen usando la ecuación de la lente. La ecuación de la lente es 1/f = 1/d_o + 1/d_i, en donde f = la distancia focal de la lente.^{[4]
X
Fuente de investigación}
- En el problema de ejemplo, es posible usar la ecuación de la lente para encontrar d_i. Reemplaza los valores de f y d_o y resuelve:
  
  1/f = 1/d_o + 1/d_i
  
  1/20 = 1/50 + 1/d_i
  
  5/100 - 2/100 = 1/d_i
  
  3/100 = 1/d_i
  
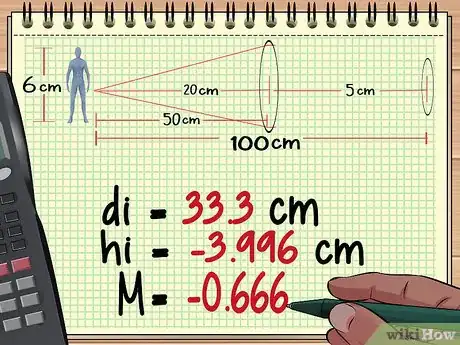
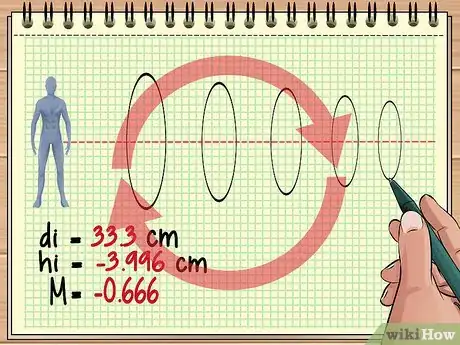
  100/3 = d_i = 33,3 centímetros
- La distancia focal de una lente constituye la distancia del centro de la lente al punto en el que los rayos de luz convergen en un punto focal. En caso de que alguna vez hayas enfocado la luz a través de una lupa para quemar hormigas, lo habrás visto. En los problemas académicos, se te suele dar esta información. En la vida real, en ocasiones es posible encontrar esta información en una etiqueta en la lente en sí.^{[5]
  X
  Fuente de investigación}
3
Encuentra h_i. Después de obtener d_o y d_i, puedes obtener la altura de la imagen aumentada y el aumento de la lente. Presta atención a los dos signos de igual en la ecuación de aumento (M = (h_i/h_o) = -(d_i/d_o)). Esto quiere decir que todos los términos son equivalentes y, por ende, es posible encontrar M y h_i en el orden que desees.^{[6]
X
Fuente de investigación}
- En el caso del problema de ejemplo, se puede encontrar h_i de la siguiente forma:
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/6) = -(33,3/50)
  
  h_i = -(33,3/50) × 6
  
  h_i = -3,996 cm
- Ten en cuenta que una altura negativa indica que la imagen que se observará estará invertida (de cabeza).
4
Encuentra M. Es posible encontrar la última variable usando ya sea -(d_i/d_o) o (h_i/h_o).
- En el ejemplo, encontrarías M finalmente de la siguiente forma:
  
  M = (h_i/h_o)
  
  M = (-3,996/6) = -0,666
- Asimismo, se obtiene la misma respuesta al usar los valores de d:
  
  M = -(d_i/d_o)
  
  M = -(33,3/50) = -0,666
- Ten en cuenta que el aumento no tiene una unidad.
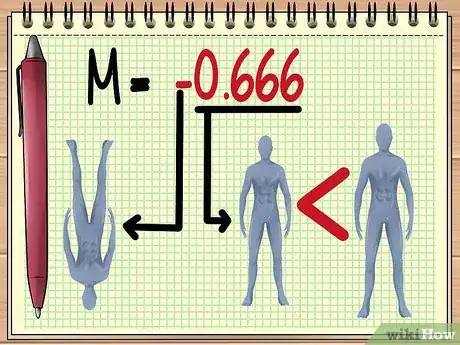
5
Interpreta el valor de M. Después de obtener un valor para el aumento, es posible predecir varias cosas en cuanto a la imagen que se observará a través de la lente. Estas son las siguientes:
- El tamaño: mientras mayor sea el valor absoluto de M, el objeto tendrá una apariencia más grande bajo el aumento. Un valor de M entre 1 y 0 indica que el objeto tendrá una apariencia más pequeña.
- La orientación: los valores negativos indican que la imagen del objeto estará invertida.
- Siguiendo con el ejemplo, el valor de M de -0,666 implica que, bajo las condiciones dadas, la imagen de la figura de acción aparecerá de cabeza y a dos tercios de su tamaño normal.
6
Usa un valor negativo para la distancia focal en el caso de las lentes divergentes. Las lentes divergentes tienen un aspecto muy distinto de las lentes convergentes, pero puedes encontrar sus valores de aumento mediante las mismas fórmulas usadas anteriormente. La única excepción importante aquí es que las lentes divergentes tendrán distancias focales negativas. En un problema como el anterior, debido a que esto tendrá un efecto sobre la respuesta que obtengas para d_i, debes tener cuidado de prestar mucha atención.^{[7]
X
Fuente de investigación}
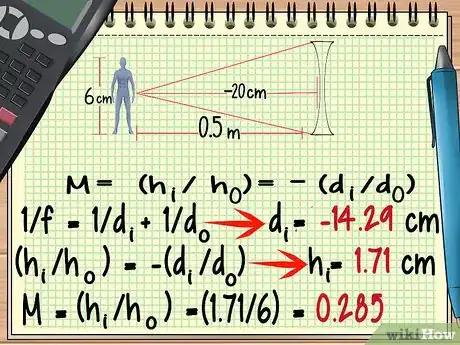
- Vuelve a realizar el problema de ejemplo anterior solo que, esta vez, imagina que se usó una lente divergente con una distancia focal de -20 centímetros. Todos los demás valores iniciales son iguales.
- En primer lugar, encuentra d_i con la ecuación de la lente:
  
  1/f = 1/d_o + 1/d_i
  
  1/-20 = 1/50 + 1/d_i
  
  -5/100 - 2/100 = 1/d_i
  
  -7/100 = 1/d_i
  
  -100/7 = d_i = -14,29 centímetros
- Ahora, encuentra h_i y M con el nuevo valor para d_i.
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/6) = -(-14,29/50)
  
  h_i = -(-14,29/50) × 6
  
  h_i = 1,71 centímetros
  
  M = (h_i/h_o)
  
  M = (1,71/6) = 0,285

Método 2

Método 2 de 2:
Encontrar el aumento de varias lentes en secuencia

Método fácil de dos lentes

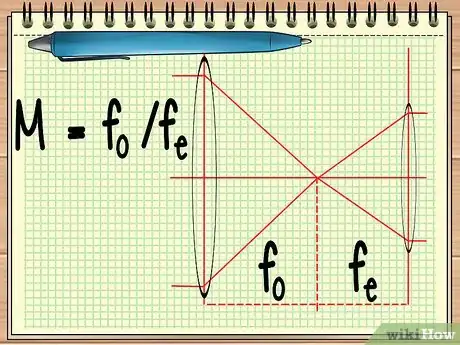
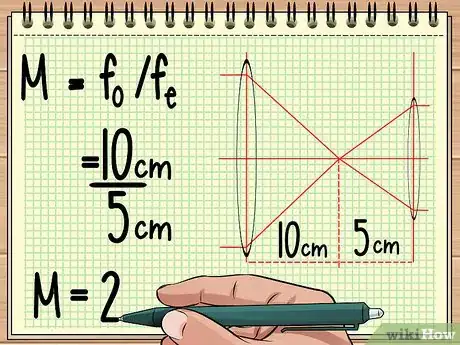
1
Encuentra la distancia focal de ambas lentes. Al lidiar con un dispositivo compuesto de dos lentes alineadas una con otra (por ejemplo, un telescopio o una parte de un par de binoculares), lo único que tienes que saber es la distancia focal de ambas lentes para así encontrar el aumento general de la imagen final. Esto se lleva a cabo mediante la ecuación simple M = f_o/f_e.^{[8]
X
Fuente de investigación}
- En la ecuación, f_o se refiere a la distancia focal de la lente objetiva, y f_e se refiere a la distancia focal de la lente ocular. La lente objetiva es la lente grande en el extremo del dispositivo, en tanto que la lente ocular, como su nombre lo indica, constituye la lente pequeña junto a la cual se coloca el ojo.
2
Reemplaza la información en M = f_o/f_e. Después de tener las distancias focales de ambas lentes, será fácil resolver. Tan solo debes encontrar la proporción dividiendo la distancia focal de la lente objetiva entre la de la lente ocular. La respuesta que obtengas constituirá el aumento del dispositivo.^{[9]
X
Fuente de investigación}
- Por ejemplo, imagina que tienes un telescopio pequeño. En caso de que la distancia focal de la lente objetiva sea de 10 centímetros y la distancia focal de la lente ocular sea de 5 centímetros, el aumento será tan solo 10/5 = 2.

Método detallado

1
Encuentra la distancia entre las lentes y el objeto. En caso de que tengas dos lentes alineadas frente a un objeto, puedes determinar el aumento de la imagen final si conoces las distancias de las lentes y los objetos en relación una con la otra, el tamaño del objeto y las distancias focales de ambas lentes. Todo lo demás puede obtenerse.^{[10]
X
Fuente de investigación}
- Por ejemplo, imagina que la disposición es la misma que en el problema de ejemplo en el método 1: una figura de acción de 15 cm (6 pulgadas) a 50 centímetros de una lente convergente con una distancia focal de 20 centímetros. Ahora, colocas una segunda lente convergente con una distancia focal de 5 centímetros a 50 centímetros por detrás de la primera lente (a 100 centímetros de la figura de acción). En los siguientes pasos, utilizarás esta información para encontrar el aumento de la imagen final.
2
Encuentra la distancia, la altura y el aumento de la imagen para la primera lente. La primera parte de cualquier problema con varias lentes es igual a si estuvieras lidiando únicamente con la primera lente. Empieza por la lente que esté más cerca del objeto y utiliza la ecuación de la lente para encontrar la distancia de la imagen. Luego, emplea la ecuación de aumento para encontrar su altura y aumento. Haz clic aquí para obtener un resumen de los problemas con una sola lente.
- De tu trabajo en el método 1 anteriormente, sabes que la primera lente produce una imagen de -3,996 centímetros de alto, 33,3 centímetros detrás de la lente y con un aumento de -0,666.
3
Utiliza la imagen de la primera lente como el objeto para la segunda. Ahora, es fácil encontrar el aumento, la altura, etc., para la segunda lente. Tan solo debes usar las mismas técnicas que usaste para la primera lente solo que, esta vez, en lugar del objeto, debes usar su imagen. Ten en cuenta que, por lo general, la distancia a la que la imagen se encuentre de la segunda lente será distinta de la distancia entre el objeto y la primera lente.^{[11]
X
Fuente de investigación}
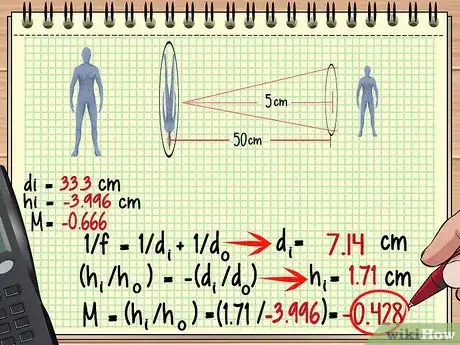
- En el ejemplo, la imagen se encuentra a 33,3 centímetros detrás de la primera lente, por lo que se encuentra a 50 - 33,3 = 16,7 centímetros frente a la segunda. Utiliza esto y la distancia focal de la nueva lente para encontrar la imagen de la segunda lente.
  
  1/f = 1/d_o + 1/d_i
  
  1/5 = 1/16,7 + 1/d_i
  
  0,2 - 0,0599 = 1/d_i
  
  0,14 = 1/d_i
  
  d_i = 7,14 centímetros
- Ahora, puedes encontrar h_i y M para la segunda lente:
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/-3,996) = -(7,14/16,7)
  
  h_i = -(0,427) × -3,996
  
  h_i = 1,71 centímetros
  
  M = (h_i/h_o)
  
  M = (1,71/-3,996) = -0,428
4
Sigue con este patrón para las lentes adicionales. Este enfoque básico es igual independientemente de que tengas tres, cuatro, cinco o cien lentes alineadas frente a un objeto. Para cada lente, debes tratar la imagen de la lente anterior como si fuera su objeto y usar la ecuación de la lente y la ecuación de aumento para encontrar las respuestas.
- Ten en cuenta que las lentes siguientes pueden seguir invirtiendo la imagen. Por ejemplo, el valor de aumento que se obtuvo anteriormente (-0,428) indica que la imagen que se observará tendrá alrededor de 4/10 del tamaño de la imagen de la primera lente, pero estará por el lado correcto, ya que la imagen de la primera lente estaba de cabeza.

Consejos

Por lo general, los binoculares se especifican como un número por otro número. Por ejemplo, los binoculares pueden especificarse como 8 x 25 o 8 x 40. Cuando se hace una especificación como esta, el primer número constituye el aumento de los binoculares. No importa que el segundo número sea distinto en los ejemplos dados, ya que ambos binoculares tienen un aumento de 8. El segundo número se refiere a la claridad de la imagen que presentan los binoculares.
Ten en cuenta que, para una herramienta de aumento de una sola lente, el aumento será un número negativo en caso de que la distancia al objeto sea mayor que la distancia focal de la lente. Esto no implica que el tamaño aparente del objeto se reducirá. En este caso, el aumento ocurrirá, pero el observador verá la imagen de cabeza.