Cómo calcular el beneficio máximo

Coescrito por Personal de wikiHow

Los estadistas de negocios saben cómo emplear datos de ventas para definir funciones matemáticas para las ventas y la demanda. Mediante estas funciones y algún cálculo básico, es posible calcular el beneficio máximo que puede esperar la compañía. Si conoces la función del beneficio, puedes hallar la primera derivada de la función y luego determinar el máximo de esta.

Parte 1

Parte 1 de 3:
Utilizar la función del beneficio

1
Comprende la relación entre precio y demanda. El estudio de la economía muestra que, en la mayor parte de los negocios tradicionales, cuando aumenta la demanda de un artículo, el precio de este debe disminuir; y, a la inversa, cuando el precio disminuye, la demanda debe aumentar. Con el empleo de datos de ventas reales, una compañía puede desarrollar una gráfica de oferta y demanda, además de calcular una función del precio.^{[1]
X
Fuente de investigación}
- Puedes navegar en internet para obtener más información sobre la representación gráfica de datos de oferta y demanda.
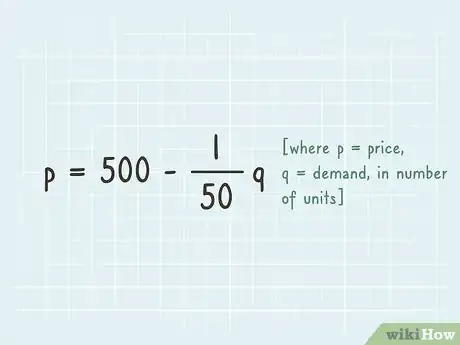
2
Crea una función del precio. La función del precio se compone de dos datos principales: el primero es la intersección, que es el precio teórico si no se vende ningún artículo, y el segundo es una pendiente decreciente. La pendiente de la gráfica representa la caída del precio de cada artículo. Una función del precio como ejemplo podría ser la siguiente:^{[2]
X
Fuente de investigación}
- $p=500-{\frac {1}{50}}q$ $p=500-{\frac {1}{50}}q$
  - p = precio
  - q = demanda, en número de unidades
- Esta función establece el “precio cero” en 500 $. Por cada unidad vendida, el precio disminuye en 1/50 de dólar (dos centavos).
3
Determina la función del beneficio. El beneficio equivale al precio del producto multiplicado por el número de unidades vendidas. Como la función del precio incluye el número de unidades, dará como resultado una variable al cuadrado. Con la función del precio anterior, la función de beneficio quedaría así:^{[3]
X
Fuente de investigación}
- $R(q)=p*q$
- $R(q)=[500-{\frac {1}{50}}q]*q$
- $R(q)=500q-{\frac {1}{50}}q^{2}$

Parte 2

Parte 2 de 3:
Hallar el valor del beneficio máximo

1
Halla la primera derivada de la función del beneficio. En cálculo, la derivada de cualquier función se utiliza para hallar la tasa de variación de dicha función. El valor máximo de una función dada se alcanza cuando la derivada es igual a cero. Por lo tanto, para maximizar el beneficio, halla la primera derivada de la función del beneficio.^{[4]
X
Fuente de investigación}
- Supón que la función del beneficio, en términos del número de unidades vendidas, es $R(q)=500q-{\frac {1}{50}}q^{2}$ $R(q)=500q-{\frac {1}{50}}q^{2}$ . La primera derivada, por tanto, es:
  - $R^{\prime }(q)=500-{\frac {2}{50}}q$
- Para repasar las derivadas, lee el artículo de wikiHow sobre cómo calcular derivadas.
2
Iguala la derivada a 0. Cuando la derivada es cero, la gráfica de la función original forma una cresta o valle, lo que representará el valor máximo o mínimo. Para algunas funciones de nivel superior, puede haber más de una solución para la derivada de cero, pero no una función básica de precio y demanda.^{[5]
X
Fuente de investigación}
- $R^{\prime }(q)=500-{\frac {2}{50}}q$
- $0=500-{\frac {2}{50}}q$
3
Despeja el número de artículos en el valor 0. Usa álgebra básica para resolver la derivada del número de artículos para vender, donde la derivada sea igual a cero. De esta forma, obtendrás el número de artículos que maximizarán el beneficio.^{[6]
X
Fuente de investigación}
- $0=500-{\frac {2}{50}}q$
- ${\frac {2}{50}}q=500$
- ${\frac {1}{50}}q=250$
- $q=50*250$
- $q=12500$
4
Calcula el precio máximo. Mediante el número óptimo de ventas del cálculo de la derivada, puedes introducir ese valor en la fórmula del precio original para hallar el precio óptimo.^{[7]
X
Fuente de investigación}
- $p=500-{\frac {1}{50}}q$
- $p=500-{\frac {1}{50}}12500$
- $p=500-250$
- $p=250$
5
Combina los resultados para calcular el beneficio máximo. Después de hallar el número de ventas y el precio óptimos, multiplícalos para hallar el beneficio máximo. Recuerda que $R=p*q$ $R=p*q$ . El beneficio máximo de este ejemplo es por tanto:^{[8]
X
Fuente de investigación}
- $R=p*q$
- $R=(250)(12500)$
- $R=3125000$
6
Haz un resumen de los resultados. Según estos cálculos, el número óptimo de unidades para vender es 12 500 al precio óptimo de $250 cada una, lo que dará como resultado un beneficio máximo de $3 125 000 en este problema de ejemplo.

Parte 3

Parte 3 de 3:
Resolver otro problema de ejemplo

1
Empieza con la función del precio. Imagina que otra empresa ha recopilado datos de precio y venta. Mediante dichos datos, la compañía ha determinado que el precio inicial es $100 y cada unidad adicional vendida reducirá el precio en un centavo. Con estos datos, la siguiente función del precio es:
- $p=100-0,01q$
2
Determina la función del beneficio. Recuerda que el beneficio es igual al precio multiplicado por la cantidad. Con la función del precio anterior, la función del beneficio es:
- $R(q)=[100-0,01q]*q$
- $R(q)=100q-0,01q^{2}$
3
Halla la derivada de la función del beneficio. Mediante el cálculo básico, halla la derivada de la función del beneficio:
- $R(q)=100q-0,01q^{2}$
- $R^{\prime }(q)=100-(2)0,01q$
- $R^{\prime }(q)=100-0,02q$
4
Halla el valor máximo. Iguala la derivada a cero y despeja $q$ $q$ para hallar el número óptimo de ventas. Este cálculo sería el siguiente:
- $R^{\prime }(q)=100-0,02q$
- $0=100-0,02q$
- $0,02q=100$
- $q=100/0,02$
- $q=5000$
5
Calcula el precio óptimo. Utiliza el valor de ventas óptimo en la fórmula del precio original para hallar el precio óptimo de ventas. Para esta ejemplo, funcionaría del siguiente modo:
- $p=100-0,01q$
- $p=100-0,01(5000)$
- $p=100-50$
- $p=50$
6
Combina las ventas máximas y el precio óptimo para hallar el beneficio máximo. Teniendo en cuenta la relación de que el beneficio es igual al precio multiplicado por la cantidad, puedes hallar el beneficio máximo como sigue:
- $R(q)=p*q$
- $R(q)=50*5000$
- $R(q)=250000$
7
Interpreta los resultados. Mediante estos datos y según la función del precio $p=100-0,01q$ , el beneficio máximo de la empresa es $250 000, lo que supone un precio por unidad de $50 y una venta de 5000 unidades.