Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 172 728 veces.
El centro de gravedad o centroide, es el punto en el cual se equilibra la masa de un triángulo. Para ayudarte a comprender mejor este concepto, imagina que tienes una baldosa triangular suspendida sobre la punta de un lápiz. La baldosa se mantendrá en equilibrio si la punta del lápiz se coloca justo en el centro de gravedad. Este dato tiene varios usos en el campo de la ingeniería y el diseño. Para hallarlo, solo tienes que usar simples operaciones geométricas.
Pasos
Método 1
Método 1 de 3:Usar el punto de intersección de las medianas
-
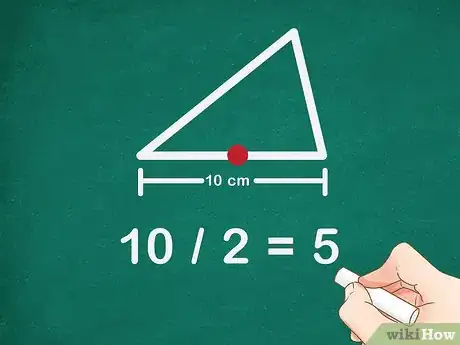
1Busca el punto medio de uno de los lados del triángulo. Para hallar el punto medio, mide el lado y divide la longitud por dos. Etiqueta el punto medio con la letra A.
- Por ejemplo, si uno de los lados del triángulo mide 10 cm, el punto medio se encontrará a los 5 cm ya que .
-
2Busca el punto medio de otro de los lados del triángulo. Mide la longitud del lado y divídela por dos. Etiqueta el punto medio con la letra B.
- Por ejemplo, si otro de los lados del triángulo es de 12 cm de largo, el punto medio se encontrará a los 6 cm ya que .
-
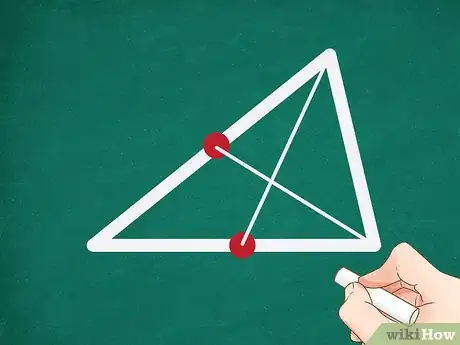
3Dibuja una línea desde el punto medio de cada lado hasta el vértice opuesto. Estas dos líneas serán las medianas de cada lado.[1]
- El vértice es el punto donde se unen dos lados del triángulo.
-
4Dibuja un punto en la intersección de las dos medianas. Ese punto es el centro de gravedad del triángulo, también conocido como "centroide" o centro de masa.[2] [3]
- El centro de gravedad es donde se intersecan las tres medianas, pero como las medianas solo se intersecan en un punto, puedes usar un atajo y encontrar el centro de gravedad a través de la intersección de solo dos medianas.
Método 2
Método 2 de 3:Usar la relación 2:1
-
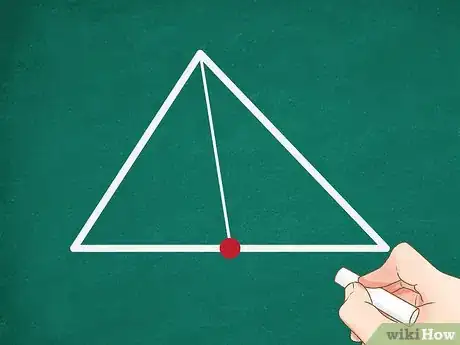
1Dibuja una mediana del triángulo. Recuerda que la mediana es una línea perpendicular que va desde el punto medio de un lado hasta el vértice opuesto. Puedes la mediana de cualquier lado del triángulo.
-
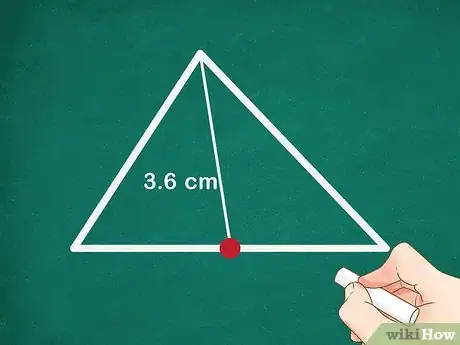
2Mide la longitud de la mediana. Asegúrate de que la medida sea exacta.
- Por ejemplo, puedes tener una mediana de 3,6 cm de longitud.
-
3Divide la longitud de la mediana en tres partes iguales. Para hacerlo, divide la longitud por tres. Una vez más, asegúrate de que la medida sea exacta. Si redondeas, no encontrarás el centro de gravedad exacto.
- Por ejemplo, si la mediana es de 3,6 cm de longitud, debes dividir 3,6 por 3:
, por lo tanto, ⅓ de la mediana medirá 1,2 cm.
- Por ejemplo, si la mediana es de 3,6 cm de longitud, debes dividir 3,6 por 3:
-
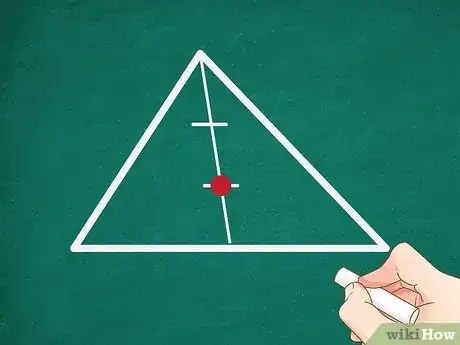
4Marca un punto de la mediana a ⅓ del punto medio. Este punto es el centroide del triángulo, que siempre divide la mediana en una relación de 2:1. Esto significa que el centroide está a ⅓ de mediana de distancia del punto medio y a ⅔ de mediana de distancia del vértice.[4]
- Por ejemplo, para una mediana de 3,6 cm de longitud, el centroide estará a 1,2 cm del punto medio.
Método 3
Método 3 de 3:Usar un promedio de coordenadas
-
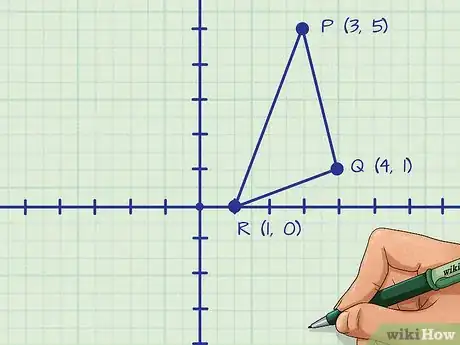
1Determina las coordenadas de los tres vértices del triángulo. Este método solo funciona si vas a trabajar en un plano de coordenadas. Es posible que te den las coordenadas, o también podrían darte un triángulo dibujado en un gráfico sin las coordenadas etiquetadas. Recuerda que las coordenadas siempre se expresan de la forma .
- Por ejemplo, podrían darte un triángulo PQR para que encuentres y etiquetes el punto P (3,5), el punto Q (4,1) y el punto R (1,0).
-
2Suma los valores de las coordenadas en . Recuerda sumar las tres coordenadas. No podrás calcular correctamente el centro de gravedad si usas solo dos coordenadas.
- Por ejemplo, si tus tres coordenadas en son 3, 4 y 1, suma estos tres valores: .
-
3Suma los valores de las coordenadas en . Recuerda que tienes que sumar las tres coordenadas.
- Por ejemplo, si tus tres coordenadas en son 5, 1 y 0, suma estos tres valores: .
-
4Calcula el promedio de las coordenadas en y en . Estas coordenadas serán las coordenadas del centro de gravedad del triángulo, también conocido como centroide o centro de masa. [5] Para calcular el promedio, divide la suma de las coordenadas por 3.
- Por ejemplo, si la suma de coordenadas en es 8, el promedio de coordenadas en será . Si la suma de coordenadas en y es 6, el promedio de coordenadas será , o .
-
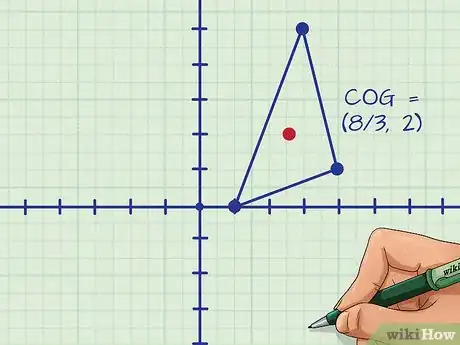
5Dibuja el centro de gravedad en el triángulo. El centro de gravedad o centroide es el promedio de coordenadas en y en .
- En el problema de ejemplo, el centro de gravedad es el punto .
Consejos
- No importa qué lado elijas, el centro de gravedad siempre estará en el mismo punto. Si sigues los pasos de este proceso para los tres lados, las líneas se cruzarán en un solo punto.
Referencias
- ↑ http://jwilson.coe.uga.edu/EMAT6680Fa06/Chitsonga/MEDIAN/THE%20MEDIANS%20OF%20A%20TRIANGLE.htm
- ↑ http://jwilson.coe.uga.edu/emat6680su09/park/As4dspark/As4dspark.html
- ↑ https://www.mathsisfun.com/geometry/triangle-centers.html
- ↑ http://jwilson.coe.uga.edu/emat6680su09/park/As4dspark/As4dspark.html
- ↑ https://www.khanacademy.org/math/geometry/triangle-properties/medians-centroids/v/triangle-medians-and-centroids





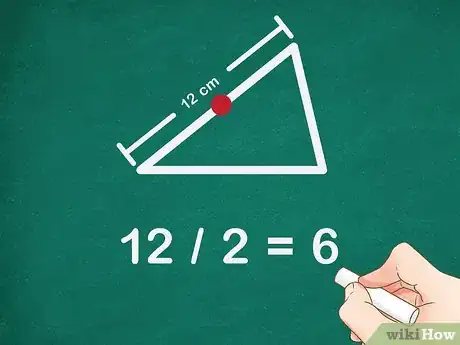





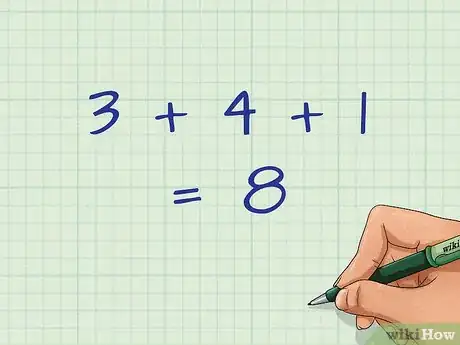


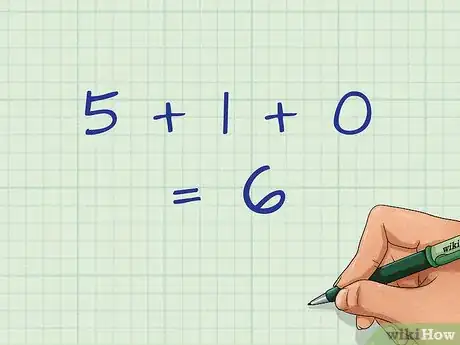


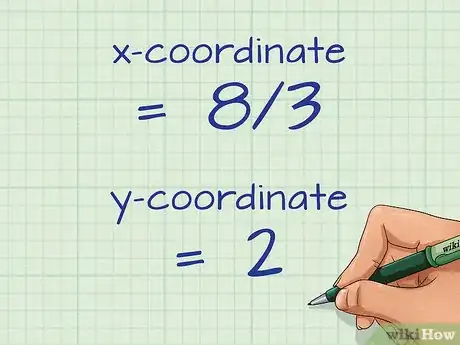























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 172 728 veces.