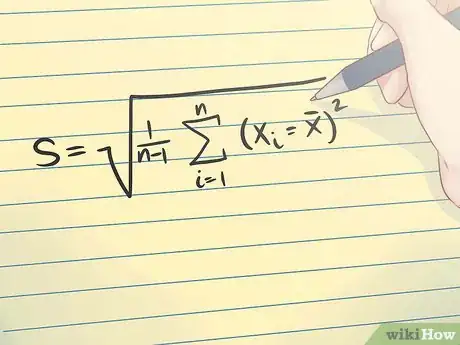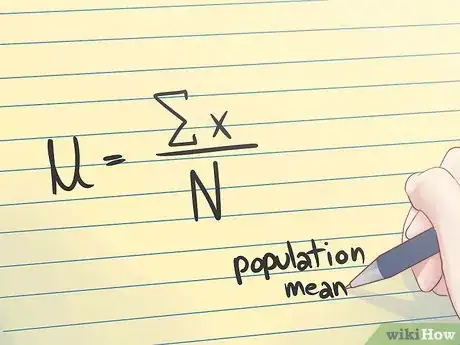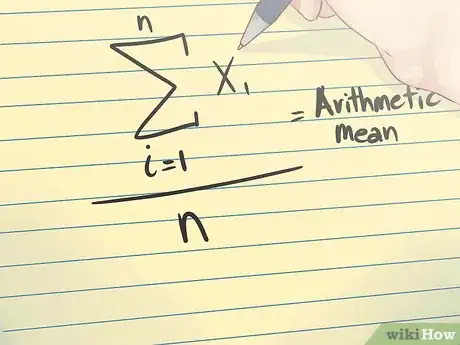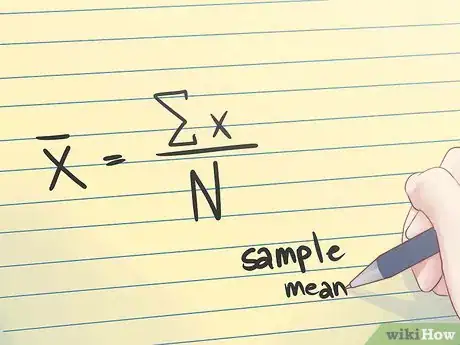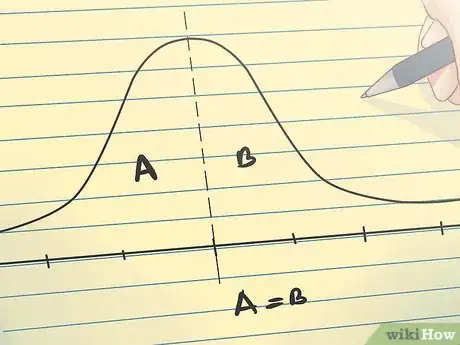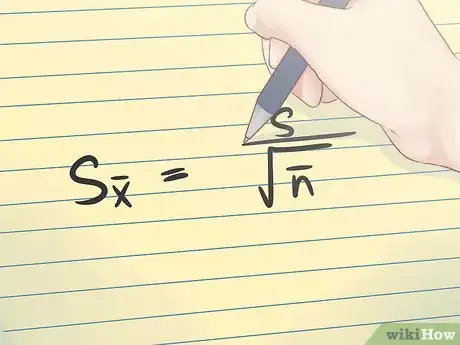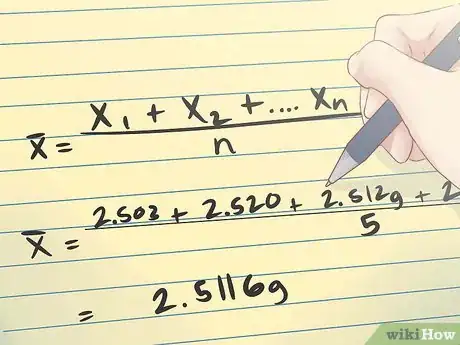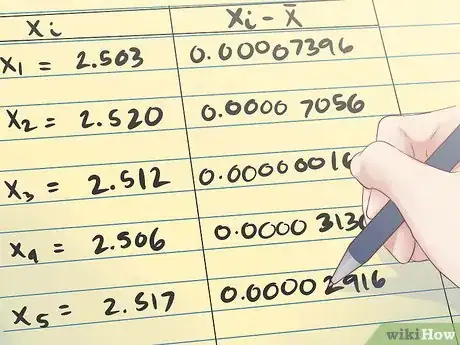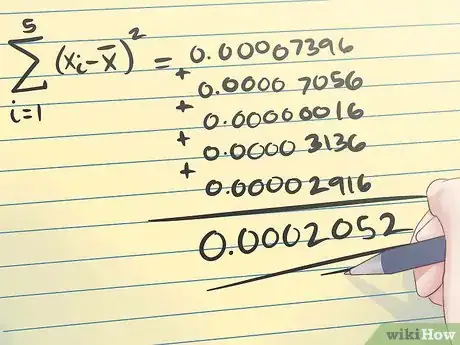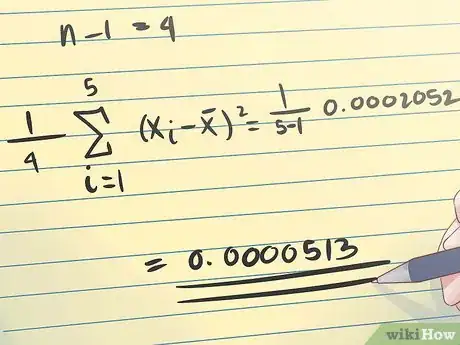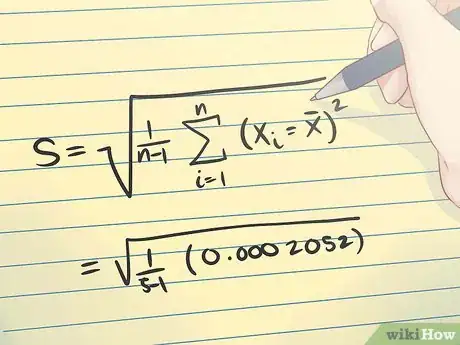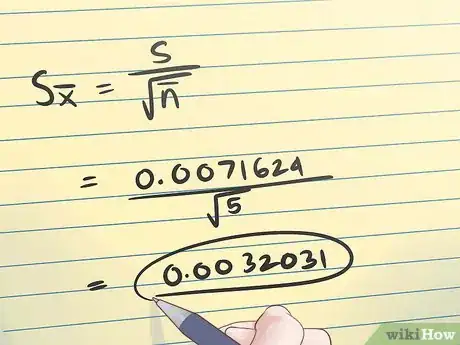Cómo calcular el error estándar

El “error estándar” se refiere a la desviación estándar de la distribución muestral de un estadístico. En otras palabras, puede usarse para medir la precisión de la media muestral. Varios usos del error estándar asumen implícitamente una distribución normal. Si necesitas calcular el error estándar, lee los pasos a continuación.

Parte 1

Parte 1 de 3:
Entender los principios básicos

1
Entiende la desviación estándar. La desviación estándar de una muestra es una medida de la dispersión de los datos. Una desviación estándar muestral generalmente se denota con una s. La fórmula matemática para la desviación estándar se muestra en la imagen de arriba.
2
Identifica la media poblacional. La media poblacional es la media de un conjunto de datos que incluye todos los elementos de la totalidad del grupo. En otras palabras, es el promedio de todo el conjunto de datos, en lugar del de solo una muestra.
3
Aprende a calcular la media aritmética. La media aritmética es simplemente un promedio: la suma de una colección de valores dividida entre el número de valores en la colección.
4
Reconoce las medias muestrales. Cuando una media aritmética se basa en una serie de observaciones obtenidas mediante el muestreo de una población estadística, se denomina “Media muestral”. Es el promedio de un conjunto de valores que incluye el promedio de solo una porción de los valores en el grupo. Se denota como se indica en la imagen de arriba.
5
Entiende la distribución normal. Las distribuciones normales, que son las distribuciones más comúnmente usadas, son simétricas y tienen un solo pico al centro que coincide con la media (o promedio) de los datos. La forma de la curva es similar a una campana, con el gráfico descendiendo uniformemente a cada lado de la media. El 50 % de la distribución se encuentra a la izquierda de la media y el otro 50 % se encuentra a su derecha. La dispersión de una distribución normal se rige por la desviación estándar.
6
Conoce la fórmula básica. La fórmula para el error estándar de una media muestral se muestra en la imagen de arriba.

Anuncio

Parte 2

Parte 2 de 3:
Calcular la desviación estándar

1
Calcula la media muestral. Para hallar el error estándar, primero debes determinar el valor la desviación estándar (porque la desviación estándar, s, es parte de la fórmula para calcular el error estándar). Comienza calculando el promedio de las variables de tu muestra. La media muestral se expresa como la media aritmética de las medidas x1, x2, . . . xn. Se calcula con la fórmula que se muestra en la imagen de arriba.
- Por ejemplo, digamos que necesitas calcular el error estándar de una media muestral del peso de cinco monedas, cuyos datos se enumeran en la tabla que se muestra en la imagen de arriba.
  Calcula la media muestral colocando en la fórmula los valores que corresponden al peso de las monedas, del modo que se muestra en la imagen arriba.
2
Resta la media muestral a cada medida y eleva al cuadrado el resultado. Una vez que tengas la media muestral, puedes expandir tu tabla restándole la media muestral a cada medida individual y luego elevando al cuadrado el resultado.
- En el ejemplo anterior, la tabla expandida se verá como se muestra en la imagen de arriba.
3
Encuentra la desviación estándar de tus medidas a partir de la media muestral. La desviación total es el promedio de estas diferencias respecto a la media muestral elevadas al cuadrado. Suma los nuevos valores para hallarla.
- En el ejemplo anterior, el cálculo se realizará del modo que se indica en la imagen de arriba.
  Esta ecuación te da el total de la desviación cuadrática de las medidas respecto a la media muestral. Date cuenta de que el signo de las diferencias no es importante.
4
Calcula la desviación cuadrática promedio de tus medidas a partir de la media muestral. Una vez que conozcas la desviación total, puedes hallar la desviación promedio dividiéndola entre n-1. Date cuenta de que n es igual al número de medidas.
- En el ejemplo anterior, tienes cinco medidas, así que n-1 será igual a 4. Haz los cálculos del modo en que se indica en la imagen de arriba.
5
Halla la desviación estándar. Ahora tienes todos los valores necesarios para usar la fórmula para calcular la desviación estándar, s.
- En el ejemplo anterior, la desviación estándar se calcula como se indica en la imagen de arriba.
Anuncio

Parte 3

Parte 3 de 3:
Hallar el error estándar

1
Utiliza la desviación estándar para calcular el error estándar, usando la fórmula básica.
- En el ejemplo anterior, el error estándar se calcula como se indica en la imagen de arriba.
  Por lo tanto, el error estándar (la desviación estándar de la media muestral) es 0,0032031 gramos.

Consejos

A menudo, se confunde el error estándar con la desviación estándar. Ten en cuenta que el error estándar describe la desviación estándar de la distribución muestral de un estadístico, no la distribución de los valores individuales.
En las revistas especializadas, el error estándar y la desviación estándar a veces se combinan. Normalmente se utiliza el símbolo ± para unir ambas medidas.

Anuncio