Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 132 816 veces.
Cuando se habla de precisión, se hace referencia a una medición realizada con una herramienta o implemento en particular y cuyo resultado siempre es similar cada vez que se lleva a cabo. Por ejemplo, si te paras sobre una balanza precisa cinco veces seguidas, esta siempre dará el mismo resultado. En el mundo de las matemáticas y las ciencias, la precisión es muy importante para determinar si tus herramientas y medidas funcionan lo suficientemente bien para obtener datos aceptables. Puedes expresar la precisión de cualquier dato utilizando el rango de valores, la desviación media o la desviación estándar.
Pasos
Método 1
Método 1 de 4:Calcular el rango
-
1Determina el valor medido más alto. Lo más recomendables es comenzar ordenando los datos en orden numérico, desde el menor al mayor, ya que, de esta manera, te asegurarás de no omitir ningún valor. Luego, selecciona el valor al final de la lista.
- Por ejemplo, supongamos que quieres probar la precisión de una balanza y tienes cinco mediciones: 11, 13, 12, 14, 12. Después de ordenar los valores, estos se expresarán de la siguiente manera 11, 12, 12, 13, 14. La medición más alta es 14.
-
2Halla el valor medido más bajo. Después de ordenar los datos, para hallar el valor más bajo, solo deberás ver el inicio de la lista.
- En el caso de los datos concernientes a la medida de la balanza, el valor más bajo es 11.
-
3Resta el valor más bajo del más alto. El rango de un conjunto de datos es la diferencia entre la medida más alta y la más baja. Lo único que deberás hacer es restar uno del otro. En términos algebraicos, el rango puede expresarse de la siguiente manera:
- En el caso de estos datos, el rango es el siguiente:
-
4Expresa el rango como la precisión. Al momento de expresar los datos, es importante que les indiques a los lectores las mediciones que has realizado. Debido a que existen diferentes medidas de precisión, debes especificar lo que estás expresando. En este caso, deberás expresar lo siguiente: media=12,4; rango=3, o simplemente media=12,4±3.[1]
- La media no es realmente parte del cálculo del rango o la precisión, sino que suele ser el cálculo principal para expresar el valor medido. Para hallarla, suma los valores medidos y luego divide el resultado entre la cantidad de elementos en el grupo. En este caso, la media es (11+13+12+14+12)/5=12,4.
Método 2
Método 2 de 4:Calcular la desviación media
-
1Halla la media de los datos. La desviación media es una medición más detallada de la precisión de un grupo de medidas o valores experimentales. El primer paso para hallar la desviación media es calcular la media de los valores medidos. La media es la suma de los valores dividida entre la cantidad de medidas tomadas.
- En este ejemplo, utiliza los mismos datos que en el ejemplo anterior. Supongamos que se han tomado cinco medidas: 11, 13, 12, 14 y 12. La media de estos valores es (11+13+12+14+12)/5=12,4.
-
2Calcula la desviación absoluta de cada valor a partir de la media. Para calcular esta precisión, será necesario que determines la cercanía de cada valor a la media. Para ello, resta la media de cada número. En el caso de esta medida, no importa si el valor está por encima o por debajo de la media. Resta los números y utiliza simplemente el valor positivo del resultado. A esto también se le denomina valor absoluto.[2]
- En términos algebraicos, el valor absoluto se muestra encerrando el cálculo entre dos barras verticales, de la siguiente manera:
- En este cálculo, representa cada uno de los valores experimentales y es la media calculada.
- Para los valores de este conjunto de datos, las desviaciones absolutas son:
- En términos algebraicos, el valor absoluto se muestra encerrando el cálculo entre dos barras verticales, de la siguiente manera:
-
3Halla la desviación media. Utiliza las desviaciones absolutas y halla su media. Tal como hiciste con el conjunto de datos original, las sumarás y dividirás el resultado entre el número de valores. La forma algebraica de representar esto es la siguiente:[3]
- En el caso de estos datos, el cálculo es el siguiente:
-
4Expresa el resultado de la precisión. Puedes expresar este resultado como la media, más o menos la desviación media. En el caso de este conjunto de datos, este resultado sería el siguiente: 12,4±0,88. Ten en cuenta que expresar la precisión como la desviación media hace que la medición parezca mucho más precisa que con el rango.[4]
Método 3
Método 3 de 4:Calcular la desviación estándar
-
1Emplea la fórmula correcta para la desviación estándar. En el caso de conjuntos de datos de cualquier tamaño, la desviación estándar es una estadística confiable para expresar la precisión. Existen dos fórmulas muy similares para calcular la desviación estándar. Utilizarás una fórmula si los datos medidos representan una población completa, mientras que la segunda sirve en caso de que los datos medidos provengan de solo una muestra de la población.[5]
- Los datos representarán a una población completa en caso de que hayas recopilado todas las medidas posibles de todos los sujetos de prueba posibles. Por ejemplo, si vas a realizar pruebas en personas que tienen alguna enfermedad muy rara y crees que has evaluado a todos los que la padecen, entonces cuentas con la población completa. En este caso, la fórmula para la desviación estándar es la siguiente:
- Un conjunto de muestras es cualquier grupo de datos menor que una población completa. En realidad, este es el que se utilizará con más frecuencia. La fórmula para la desviación estándar que se utilizará para un conjunto de muestras es la siguiente:
- Ten en cuenta que la única diferencia es en el denominador de la fracción. En el caso de una población completa, deberás dividir entre . En el caso de un conjunto de muestra, deberás dividir entre .
- Los datos representarán a una población completa en caso de que hayas recopilado todas las medidas posibles de todos los sujetos de prueba posibles. Por ejemplo, si vas a realizar pruebas en personas que tienen alguna enfermedad muy rara y crees que has evaluado a todos los que la padecen, entonces cuentas con la población completa. En este caso, la fórmula para la desviación estándar es la siguiente:
-
2Halla la media de los valores de datos. Al igual que al calcular la desviación media, deberás comenzar al hallar la media de los valores de datos.[6]
- Utilizando el mismo conjunto de medidas anterior, la media es 12,4.
-
3Halla el cuadrado de cada variación. Por cada punto de dato, resta el valor de datos de la media y eleva al cuadrado dicho resultado. Como vas a elevar al cuadrado estas variaciones, no importa si la diferencia es positiva o negativa. El cuadrado de la diferencia siempre será positivo.
- En el caso de los cinco valores de datos en esta muestra, estos cálculos son los siguientes:
- En el caso de los cinco valores de datos en esta muestra, estos cálculos son los siguientes:
-
4Calcula la suma de las diferencias de los cuadrados. El numerador de la fracción de la desviación estándar es la suma de las diferencias de los cuadrados entre cada valor y la media. Para hallar esta suma, suma las cifras del cálculo anterior.[7]
- En el caso del conjunto de datos, la suma es la siguiente:
- En el caso del conjunto de datos, la suma es la siguiente:
-
5Divide entre el tamaño de los datos. Este el único paso que variará dependiendo del cálculo de una población o un conjunto de datos. En el caso de una población completa, deberás dividir el número de valores entre . En el caso de un conjunto de datos, deberás dividir entre .[8]
- Este ejemplo solo tiene cinco medidas y, por lo tanto, solo es un conjunto de muestra. Por lo tanto, por los cinco valores que usarás, divide entre (5-1) o 4. El resultado es .
-
6Halla la raíz cuadrada del resultado. En este punto, el cálculo representará lo que se conoce como la varianza del conjunto de datos. La desviación estándar es la raíz cuadrada de la varianza. Utiliza una calculadora para hallar la raíz cuadrada, y el resultado será la desviación estándar.[9]
-
7Expresa el resultado. Por medio de este cálculo, puedes representar la precisión de la balanza al dar la media, más o menos la desviación estándar. En el caso de estos datos, la precisión será 12,4±1,14.[10]
- La desviación estándar es quizás la medida más común de precisión. No obstante, para una mayor comprensión, sigue siendo recomendable utilizar un pie de página o paréntesis para indicar que el valor de precisión representa la desviación estándar.
Método 4
Método 4 de 4:Determinar la forma adecuada de expresar la precisión
-
1Utiliza la palabra “precisión” de la manera correcta. La precisión es un término que describe el nivel de repetibilidad de las mediciones. Al momento de recolectar un grupo de datos, ya sea al realizar una medición o por medio de un experimento de alguna clase, la precisión describirá la cercanía de los resultados de cada medición o experimento.[11]
- Ten en cuenta que la precisión no es lo mismo que exactitud. La exactitud mide qué tanto los valores experimentales se acercan al valor verdadero o teórico, mientras que la precisión mide lo cerca que están los valores medidos.
- Existe la posibilidad que los datos sean exactos pero no precisos o viceversa. Las medidas exactas están cerca del valor objetivo, pero podrían no estarlo entre sí. Las medidas precisas son cercanas entre sí, independientemente de que lo estén o no del valor objetivo.
-
2Elige la mejor medida de precisión. La palabra “precisión” no tienen un solo significado, pues puedes representarla por medio de diferentes medidas, así que necesitarás determinar la más adecuada.[12]
- Rango. En el caso de los conjuntos de datos pequeños con diez medidas o menos, el rango de los valores es una buena medida de precisión.[13] Esto es particularmente verdadero si los valores parecen agrupados de manera razonablemente cercana. Si ves uno o dos valores que parecen lejanos unos de otros, probablemente debas utilizar un cálculo diferente.
- Desviación media. La desviación media es una medida de precisión más exacta para un conjunto pequeño de valores de datos.[14]
- Desviación estándar. La desviación estándar es quizás la medida de precisión más reconocida y puede utilizarse para calcular la precisión de las medidas de una población completa o de una población de muestra.[15]
-
3Expresa los resultados con claridad. Con frecuencia, los investigadores expresarán los datos al dar la media del valor medido, seguida de una declaración de la precisión. Para demostrar la precisión, se utilizará un símbolo “±”. Esto proporcionará una indicación de la precisión, pero no le explica con claridad al lector si el número que le sigue al símbolo “±” es un rango, una desviación estándar o alguna otra medida. Para ser muy claro, debes definir qué medida de precisión usarás, ya sea en un pie de página o entre paréntesis.
- Por ejemplo, en el caso de una serie de datos, el resultado puede expresarse de la siguiente manera: 12,4±3. No obstante, una forma más explicativa de expresar los mismos datos sería la siguiente: “Media=12,4; Rango=3”.
Consejos
- Si uno de los valores de prueba es mucho más alto o bajo que el resto de los valores, no excluyas este número de tus cálculos. Incluso si se tratase de un error, son datos y deben utilizarse para realizar un cálculo adecuado.
- En este artículo, solo se utilizaron cinco valores por motivos de simplicidad matemática. No obstante, en un experimento real, deberás realizar más de cinco pruebas con la finalidad de lograr un cálculo más exacto. Mientras más realices, más cerca estarás de obtener un valor de precisión claro.
Referencias
- ↑ https://www.inorganicventures.com/accuracy-precision-mean-and-standard-deviation
- ↑ http://groups.physics.umn.edu/physed/Research/Lab%20Manuals/1101/1101%20Appendix%20B.pdf
- ↑ http://groups.physics.umn.edu/physed/Research/Lab%20Manuals/1101/1101%20Appendix%20B.pdf
- ↑ http://groups.physics.umn.edu/physed/Research/Lab%20Manuals/1101/1101%20Appendix%20B.pdf
- ↑ http://www.robertniles.com/stats/stdev.shtml
- ↑ http://www.robertniles.com/stats/stdev.shtml
- ↑ http://www.robertniles.com/stats/stdev.shtml
- ↑ http://www.robertniles.com/stats/stdev.shtml
- ↑ http://www.robertniles.com/stats/stdev.shtml
- ↑ http://www.robertniles.com/stats/stdev.shtml
- ↑ http://sciencing.com/calculate-precision-6186008.html
- ↑ http://www.digipac.ca/chemical/sigfigs/accuracy_and_precision.htm
- ↑ https://www.inorganicventures.com/accuracy-precision-mean-and-standard-deviation
- ↑ http://groups.physics.umn.edu/physed/Research/Lab%20Manuals/1101/1101%20Appendix%20B.pdf
- ↑ http://www.digipac.ca/chemical/sigfigs/accuracy_and_precision.htm






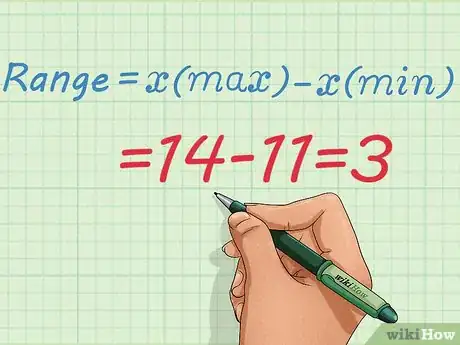


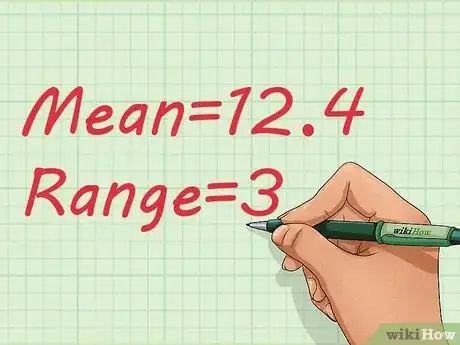




















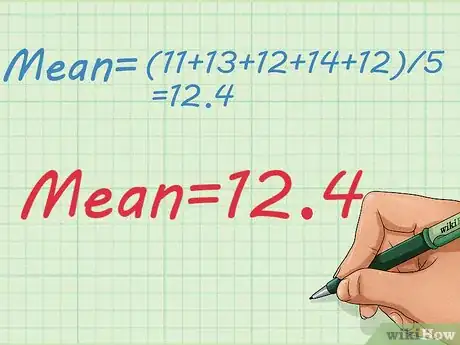
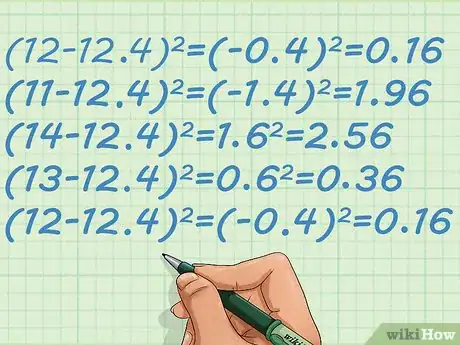




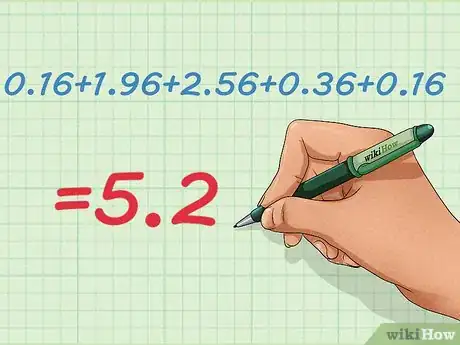

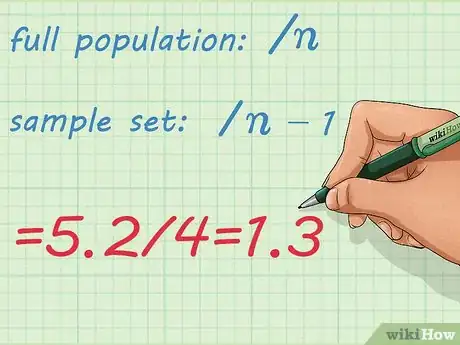

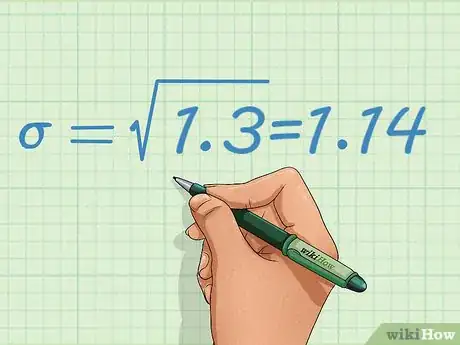
























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 132 816 veces.