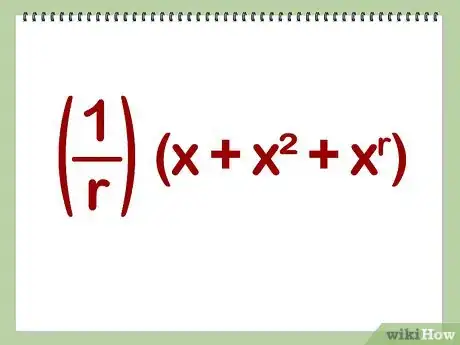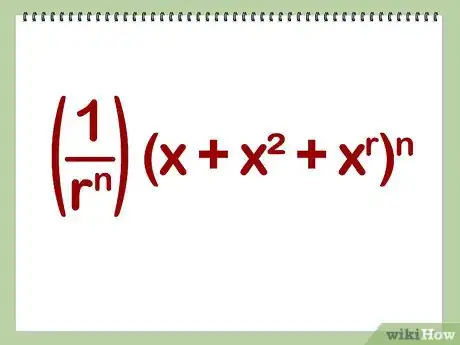Cómo calcular la probabilidades de varios dados

Información del autor

Muchas personas creen que si tiras tres dados de seis lados existe la misma probabilidad tanto de que la suma sea tres como que sea diez. Sin embargo, esto no es así y este artículo te mostrará cómo calcular la media y el desvío estándar de un conjunto de dados.

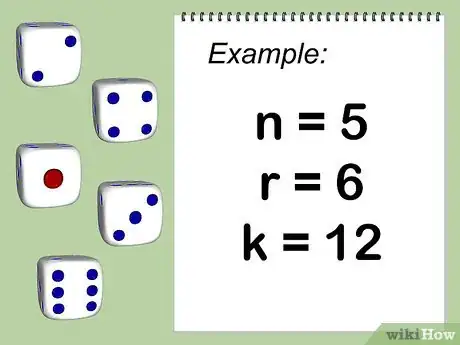
Aprende la terminología de la mecánica de dados. Por lo general, los dados utilizados son de la variedad que tiene 6 lados, pero también es común encontrar dados de las variedades d2 (monedas), d4 (pirámides de 3 lados), d8 (octaedro), d10 (decaedro), d12 (dodecaedro) y d20 (icosaedro). Un lance de dados utiliza el formato siguiente: (número de dados) (identificador de dado abreviado), así que 2d6 sería un lance de dos dados de seis lados. En este artículo, algunas fórmulas asumirán que n = número de dados idénticos y r = número de lados de cada dado, numerados desde 1 hasta r, y k es el valor de combinación. Existen varios métodos para computar la probabilidad de cada suma.

Método 1

Método 1 de 4:
Enumeración

1
Anota la cantidad de dados, sus lados y la suma deseada.
2
Enumera todas las maneras con las que puedes obtener esa suma. Esto puede resultar tedioso para una gran cantidad de dados, pero es un método bastante directo. Esto equivale a encontrar todas las combinaciones de k, dividido entre n combinaciones exactas y que ninguna de ellas sea mayor a r. En la imagen se muestra un ejemplo con n=5, r=6 y k=12. Para asegurarte de que el conteo sea exhaustivo y, a la vez, de que ninguna combinación aparezca repetida, se presentan las combinaciones en un orden lexicográfico, y los dados en cada combinación se ordenan de manera ascendente.
3
No todas las combinaciones de la lista del paso anterior tienen las mismas probabilidades. Por esta razón, debes anotarlas en una lista y no solo contarlas. En un ejemplo más pequeño de 3 dados, la combinación 123 cubre 6 posibilidades (123, 132, 213, 231, 312, 321) mientras que la combinación 114 cubre solo 3 (114, 141, 411) y 222 solo tiene una posibilidad. Utiliza la fórmula multinomial para calcular la cantidad de formas de permutar los dígitos en cada combinación. Esta información se encuentra en la tabla de la sección anterior.
4
Suma la cantidad total de formas de obtener el número deseado.
5
Divide entre el número total de resultados. Como cada dado tiene r lados posibles; esto se hace simplemente como rⁿ.

Método 2

Método 2 de 4:
Recursión

Este método brinda la probabilidad de todas las sumas para todos los números de los dados. Se puede implementar fácilmente en una hoja de cálculo.

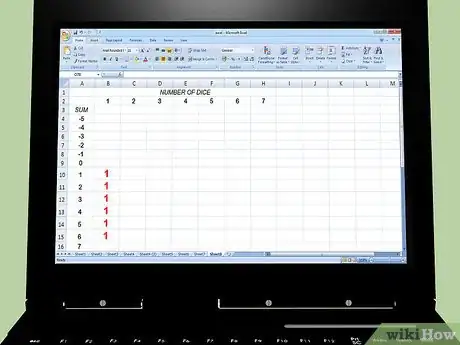
1
Anota la probabilidad de los resultados de un solo dado. Anótalos en una hoja de cálculo. En el ejemplo se utiliza un dado de 6 lados. Las filas en blanco de las sumas negativas se consideran como ceros y esto permite utilizar la misma fórmula para todas las filas.
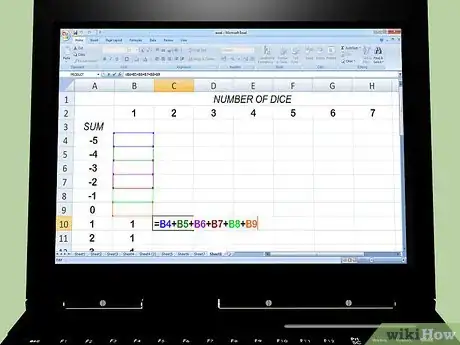
2
En la columna de 2 dados, utiliza la fórmula que se muestra en la imagen. Esta indica que la probabilidad de que 2 dados sumen un valor k cualquiera es igual a la suma de los eventos que se muestran a continuación. Para valores de k muy bajos o muy altos, es posible que algunos o todos los términos resulten cero, pero la fórmula es válida para todos los valores de k.
- El primer dado muestra k-1 y el segundo muestra 1.
- El primer dado muestra k-2 y el segundo muestra 2.
- El primer dado muestra k-3 y el segundo muestra 3.
- El primer dado muestra k-4 y el segundo muestra 4.
- El primer dado muestra k-5 y el segundo muestra 5.
- El primer dado muestra k-6 y el segundo muestra 6.
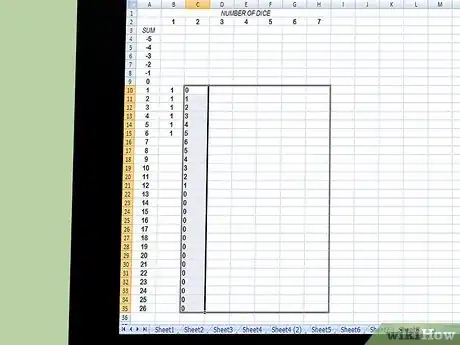
3
De la misma manera, para tres dados o más, se utiliza la misma fórmula utilizando las probabilidades, ahora conocidas, de las sumas obtenidas con un dado menos. Así, la fórmula ingresada en el paso dos también puede completarse abajo y a lo ancho hasta que la tabla contenga tanta información como sea necesaria.
4
La hoja de cálculo muestra el cálculo para la “cantidad de formas” y no la “probabilidad”, pero la conversión entre ellas es fácil: probabilidad = cantidad de formas / r^n en donde r es la cantidad de lados de cada dado y n es la cantidad de dados. Como alternativa, puedes modificar la hoja de cálculos para calcular directamente la probabilidad.

Método 3

Método 3 de 4:
Funciones generadoras

1
Escribe el polinomio (1/r)(x + x² + x^r). Esta es la función generadora para un solo dado. El coeficiente del término x^k es la probabilidad de que el dado muestre k.
2
Aumenta este polinomio a la enésima potencia para obtener la función generadora para la suma obtenida con n dados. Esto quiere decir calcular (1/rⁿ)(x + x² + x^r)ⁿ. Si n es mayor que 2 aproximadamente, entonces será conveniente que hagas esto en una computadora.
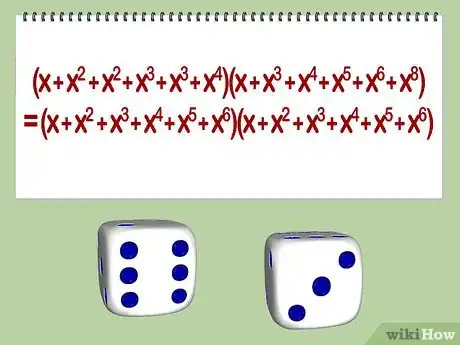
3
En términos computacionales, esto es equivalente al método anterior, pero a veces es más fácil derivar resultados teóricos utilizando una función generadora. Por ejemplo, lanzar dos dados normales de 6 lados tiene exactamente la misma distribución de sumas que un dado cuyas caras tengan escritos los números (1, 2, 2, 3, 3, 4) y que otro dado con los números (1, 3, 4, 5, 6, 8). Esto se debe a que (x+x² +x²+x³+x³+x⁴)(x+x³ +x⁴+x⁵+x⁶+x⁸) = (x+x² +x³+x⁴+x⁵+x⁶)(x+x² +x³+x⁴+x⁵+x⁶).

Método 4

Método 4 de 4:
Aproximación continua

1
Cuando se utiliza una gran cantidad de dados, el cálculo exacto utilizando los métodos anteriores puede resultar difícil. El teorema de límite central expresa que la suma de una cierta cantidad de dados idénticos se aproxima a la distribución normal a medida que aumenta la cantidad de los mismos.
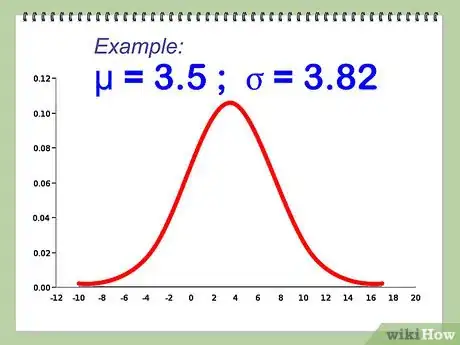
2
Calcula la media y el desvío estándar basándote en la cantidad y el tipo de dados. Considerando n dados numerados de 1 a r, se utilizan las fórmulas que aparecen a continuación.
- La media es (r+1)/2.
- La varianza es n(r^2-1)/12.
- El desvío estándar es la raíz cuadrada de la varianza.
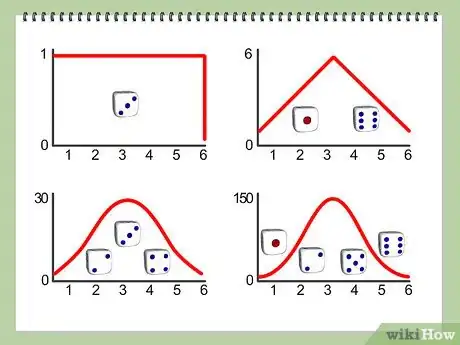
3
Utiliza la distribución normal con la media y el desvío estándar que aparecen en la imagen como una aproximación a la sumatoria de los dados.

Advertencias

Utilizar un conjunto con más de un tipo de dado hace que estos métodos se compliquen. En este caso, el método más sencillo para determinar la probabilidad generalmente es enumerar todos los resultados posibles y ordenarlos en un orden creciente según su total.