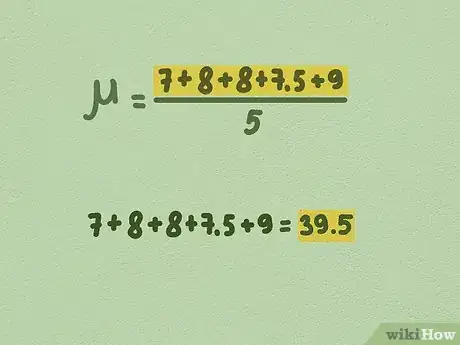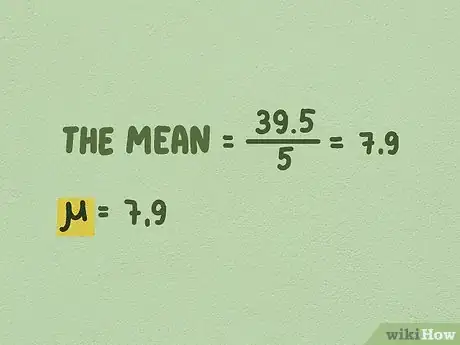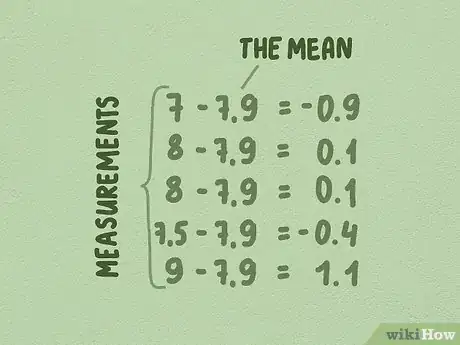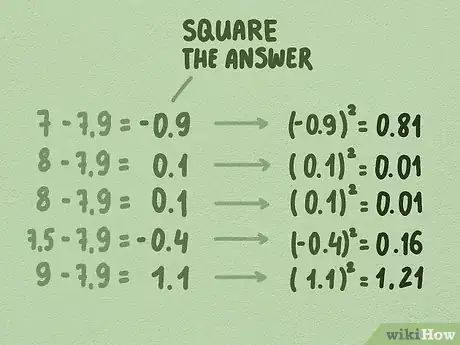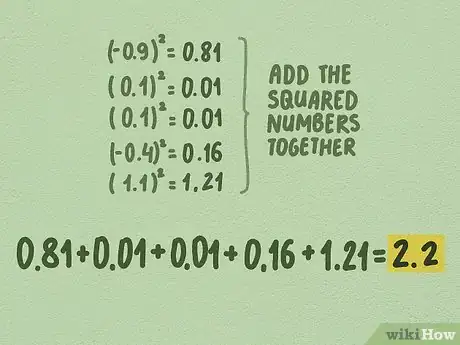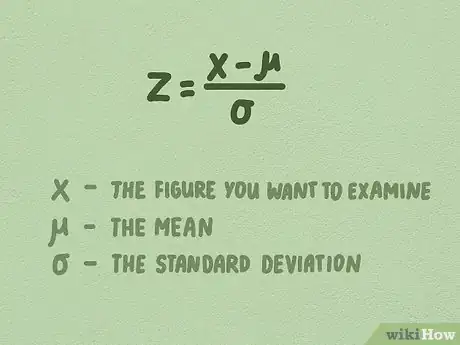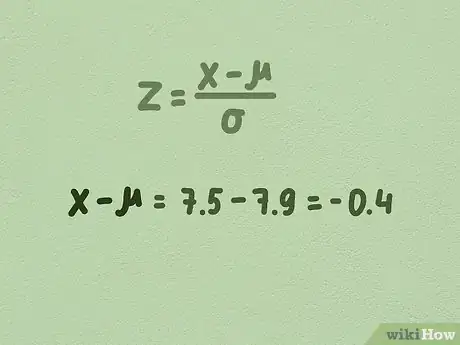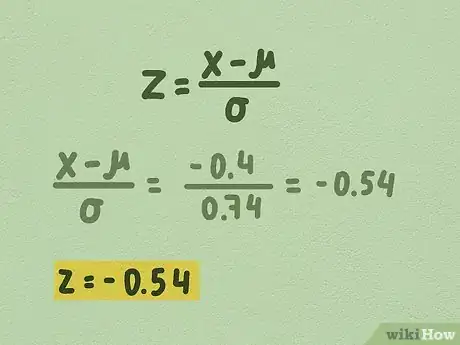Cómo calcular puntajes Z

Información del autor

Un puntaje Z te permite tomar cualquier muestra de un conjunto de datos y determinar a cuántas unidades de desviación estándar se encuentra por encima o por debajo de la media.^{[1]
X
Fuente de investigación} Para hallar el puntaje Z de una muestra, necesitarás conocer la media, la varianza y la desviación estándar de la misma. Para calcular el puntaje Z, deberás hallar la diferencia entre un valor en la muestra y la media, para luego dividirla entre la desviación estándar. A pesar de que completar este método requiere muchos pasos, se trata de un cálculo bastante simple.

Parte 1

Parte 1 de 4:
Calcular la media

1
Observa el conjunto de datos. Necesitarás algunos datos clave para calcular la media o el promedio matemático de la muestra.^{[2]
X
Fuente de investigación}
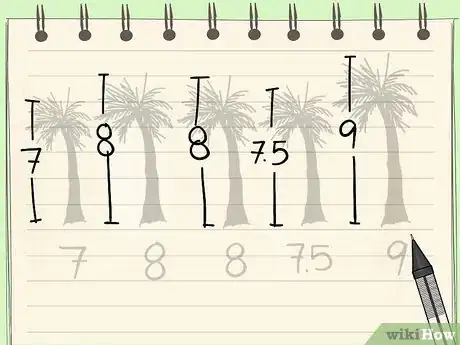
- Ten en cuenta la cantidad de números que hay en la muestra. En el caso de la presente muestra de las palmeras, existen 5 números.
- Determina lo que representan los números. En nuestro ejemplo, estos números representan a las medidas de los árboles.
- Observa la variación en los números. ¿Los datos varían por mucho o por poco?
2
Recolecta todos los datos. Necesitarás todos los números en la muestra para comenzar a realizar los cálculos.^{[3]
X
Fuente de investigación}
- La media es el promedio de todos los números en tu muestra.
- Para calcularla, deberás sumar todos los números en la muestra y luego dividir el resultado entre el tamaño de la muestra.
- En la notación matemática, “n” representa al tamaño de la muestra. En el caso de nuestra muestra con las alturas de los árboles, n = 5, ya que hay 5 números en ella.
3
Suma todos los números en la muestra. Esta es la primera parte del cálculo del promedio matemático o la media.^{[4]
X
Fuente de investigación}
- Por ejemplo, utilizando la muestra de 5 palmeras, nuestro ejemplo se compone de los siguientes números: 7, 8, 8, 7,5 y 9.
- 7 + 8 + 8 + 7,5 + 9 = 39,5. Esta es la suma de todos los números en la muestra.
- Verifica tu respuesta para asegurarte de haber sumado correctamente.
4
Divide la suma entre el tamaño de la muestra (n). Esto proporcionará el promedio o la media de los datos.^{[5]
X
Fuente de investigación}
- Por ejemplo, sigamos con nuestra muestra de las alturas de los árboles: 7, 8, 8, 7,5 y 9. Existen 5 números en nuestra muestra, así que n = 5.
- La suma de las alturas de los árboles en la muestra es de 39,5. Por lo tanto, deberás dividir esta cifra entre 5 para hallar la media.
- 39,5/5 = 7,9.
- La altura promedio de los árboles es de 7,9 unidades. La media poblacional a menudo se representa con el símbolo μ, por lo tanto, μ = 7,9.
Anuncio

Parte 2

Parte 2 de 4:
Hallar la varianza

1
Halla la varianza. La varianza es una cifra que representa la manera en que se distribuyen los datos de la muestra en la media.^{[6]
X
Fuente de investigación}
- Este cálculo te dará una idea de hasta qué punto se expanden los datos.
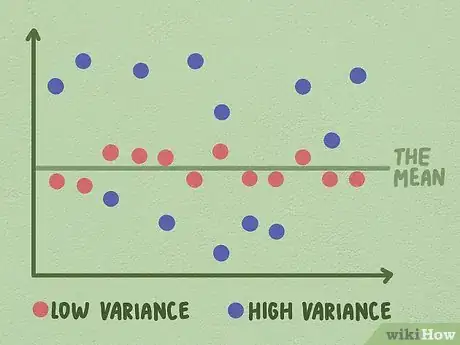
- Las muestras con una varianza baja tienen datos que se distribuyen a corta distancia alrededor de la media.
- Las muestras con una varianza alta tienen datos que se extienden más allá de la media.
- Por lo general, la varianza se utiliza para comparar las distribuciones entre dos conjuntos de datos o muestras.
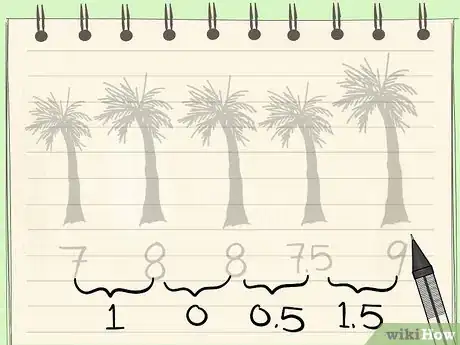
2
Resta la media de cada uno de los números en tu muestra. Esto te dará una idea de cuánto difiere de la media cada número en tu muestra.^{[7]
X
Fuente de investigación}
- En nuestra muestra de las alturas de los árboles (7, 8, 8, 7,5 y 9 unidades), la media era de 7,9.
- 7 – 7,9 = -0,9; 8 – 7,9 = 0,1; 8 – 7,9 = 0,1; 7,5 – 7,9 = -0,4 y 9 – 7,9 = 1,1
- Realiza estos cálculos nuevamente para verificar tus resultados. Es sumamente importante que tengas las cifras correctas para este paso.
3
Eleva al cuadrado todas las respuestas de las restas que acabas de hacer. Necesitarás todas estas cifras para determinar la varianza en la muestra.^{[8]
X
Fuente de investigación}
- Recuerda que en nuestra muestra restamos la media de 7,9 de cada uno de los puntos de datos (7, 8, 8, 7,5 y 9) y obtuvimos lo siguiente: -0,9, 0,1, 0,1, -0,4 y 1,1.
- Eleva al cuadrado todas estas cifras: (-0,9)^2 = 0,81; (0,1)^2 = 0,01; (0,1)^2 = 0,01; (-0,4)^2 = 0,16 y (1,1)^2 = 1,21.
- Los cuadrados de este cálculo son: 0,81, 0,01, 0,01, 0,16 y 1,21.
- Verifica tus respuestas antes de continuar con el siguiente paso.
4
Suma todos los números elevados al cuadrado. A este cálculo se le conoce como la suma de los cuadrados.^{[9]
X
Fuente de investigación}
- En nuestra muestra de las alturas de los árboles, los cuadrados fueron los siguientes: 0,81, 0,01, 0,01, 0,16 y 1,21.
- 0,81 + 0,01 + 0,01 + 0,16 + 1,21 = 2,2
- En nuestro ejemplo de las alturas de los árboles, la suma de los cuadrados es 2,2.
- Verifica la suma para asegurarte de tener la cifra correcta antes de proseguir.
5
Divide la suma de los cuadrados (n-1). Recuerda que “n” es el tamaño de la muestra (la cantidad de números que hay en la muestra). Este paso te proporcionará la varianza.^{[10]
X
Fuente de investigación}
- En la muestra de las alturas de los árboles (7, 8, 8, 7,5 y 9 unidades), la suma de los cuadrados fue 2,2.
- Existen 5 números en esta muestra. Por lo tanto, n = 5.
- n - 1 = 4
- Recuerda que la suma de los cuadrados es 2,2. Para hallar la varianza, calcula lo siguiente: 2,2 / 4.
- 2,2 / 4 = 0,55
- Por lo tanto, la varianza para esta muestra de altura de los árboles es 0,55.
Anuncio

Parte 3

Parte 3 de 4:
Calcular la desviación estándar

1
Halla la cifra de la varianza. La necesitarás con la finalidad hallar la desviación estándar para la muestra.^{[11]
X
Fuente de investigación}
- La varianza es la dispersión en la que se encuentran los datos de la media o del promedio matemático.
- La desviación estándar es una cifra que representa la dispersión de los datos en la muestra.
- En nuestro ejemplo de la altura de los árboles, la varianza fue 0,55.
2
Saca la raíz cuadrada de la varianza. Esta cifra es la desviación estándar.^{[12]
X
Fuente de investigación}
- En nuestro ejemplo de la altura de los árboles, la varianza fue 0,55.
- √0,55 = 0,741619848709566. Por lo general, al hacer este cálculo obtendrás una cifra decimal bastante grande. Puedes redondear al segundo o tercer lugar decimal para determinar la cifra de desviación estándar. En este caso, podrías utilizar la cifra 0,74.
- Empleando una cifra redondeada, la desviación estándar en nuestra muestra de la altura de los árboles será 0,74.
3
Verifica los cálculos de la media, la varianza y la desviación estándar. Esto te permitirá asegurarte de tener la cifra correcta para la desviación estándar.
- Anota todos los pasos que seguiste para realizar los cálculos.
- Esto te permitirá determinar dónde cometiste un error, en caso de que lo hayas hecho.
- Si obtuviste una cifra diferente para la media, la varianza y la desviación estándar durante el proceso de verificación, repite los cálculos con sumo cuidado.
Anuncio

Parte 4

Parte 4 de 4:
Calcular los puntajes Z

1
Utiliza el siguiente formato para hallar un puntaje Z: z = X - μ / σ. Esta fórmula te permitirá calcular un puntaje Z para cualquier dato en tu muestra.^{[13]
X
Fuente de investigación}
- Recuerda que un puntaje Z es una medida que indica a cuántas desviaciones estándares de distancia se encuentra un dato de la media.
- En la fórmula, X representa la cifra que quieres examinar. Por ejemplo, si quisieras hallar a cuántas desviaciones estándares de distancia se encuentra 7,5 de la media en el ejemplo de las alturas de los árboles, deberás reemplazar X por dicho número dentro de la ecuación.
- En la fórmula, μ representa la media. En nuestro ejemplo de las alturas de los árboles, la media fue de 7,9.
- En la fórmula, σ representa la desviación estándar. En nuestro ejemplo de las alturas de los árboles, la desviación estándar fue de 0,74.
2
Comienza a resolver la fórmula restando la media de los datos que quieres examinar. Esto dará inicio al cálculo para hallar un puntaje Z.^{[14]
X
Fuente de investigación}
- Por ejemplo, en nuestra muestra de las alturas de los árboles queremos determinar a cuántas desviaciones estándares de distancia se encuentra 7,5 de la media de 7,9.
- Por lo tanto, deberás realizar la siguiente operación: 7,5 – 7,9.
- 7,5 – 7,9 = -0,4
- Verifica los resultados antes de continuar.
3
Divide el resultado que acabas de obtener entre la desviación estándar. Este cálculo te dará el puntaje Z.^{[15]
X
Fuente de investigación}
- En nuestra muestra de las alturas de los árboles, queremos hallar el puntaje Z para el dato 7,5.
- Ya restamos la media de 7,5 y obtuvimos como resultado -0,4.
- Recuerda que la desviación estándar de nuestra muestra de alturas de los árboles fue 0,74.
- - 0,4 / 0,74 = - 0,54
- Por lo tanto, el puntaje Z en este caso es -0,54.
- Este puntaje Z indicia que 7,5 se encuentra a -0.54 desviaciones estándar de distancia de la media en la muestra de las alturas de los árboles.
- Los puntajes Z pueden ser positivos y negativos.
- Un puntaje Z negativo indica que los datos son menores que la media. Por el contrario, un puntaje Z positivo indica que los datos en cuestión son mayores que la media.
Anuncio