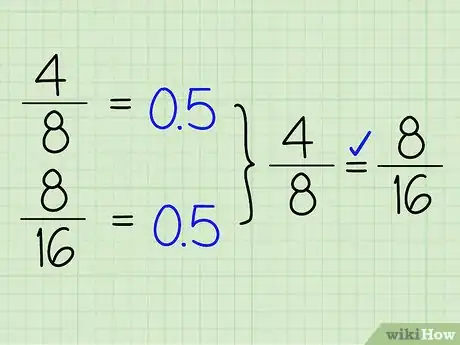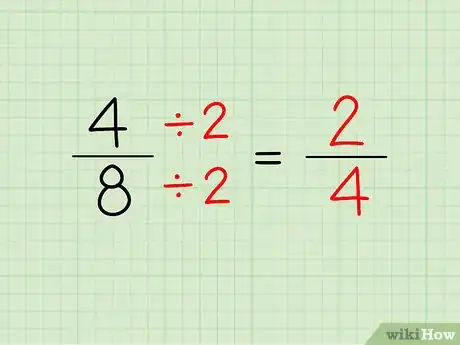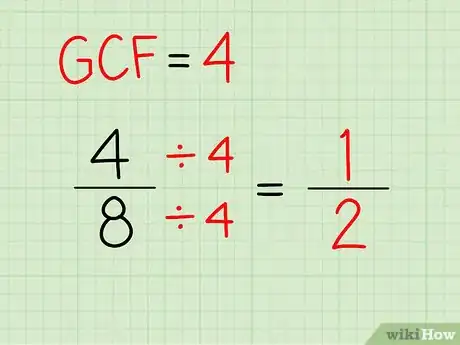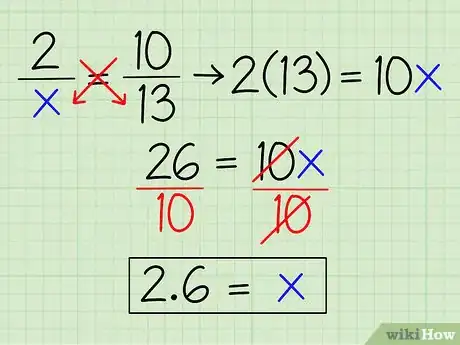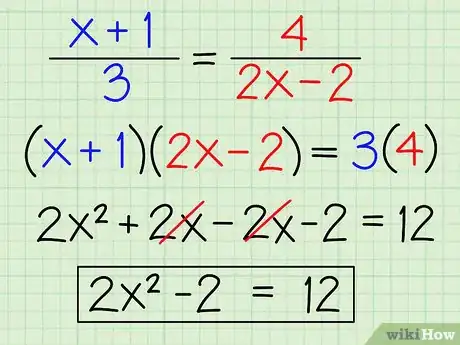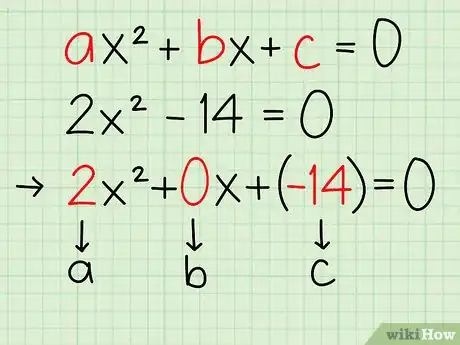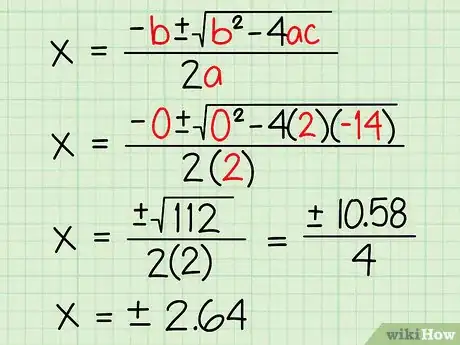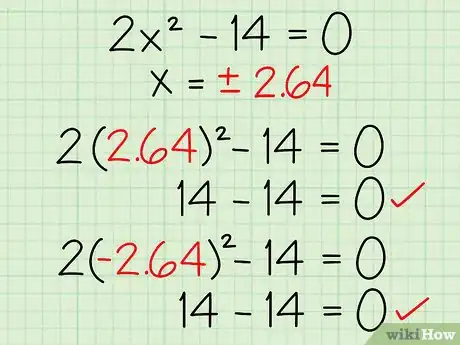Cómo convertir a fracciones equivalentes

Coescrito por David Jia

Dos fracciones son equivalentes si tienen el mismo valor. Saber cómo convertir una fracción en un equivalente es una habilidad matemática esencial y necesaria para todo, ya sea desde álgebra básica hasta cálculo avanzado. Este artículo cubrirá varios métodos para calcular fracciones equivalentes desde la multiplicación y división básica hasta métodos más complejos para resolver ecuaciones con fracciones equivalentes.

Método 1

Método 1 de 5:
Formar fracciones equivalentes

1
Multiplica el numerador y el denominador por el mismo número. Por definición, dos fracciones que son diferentes pero equivalentes tienen numeradores y denominadores que son múltiplos el uno del otro. Es decir, multiplicar el numerador y el denominador de una fracción por el mismo número dará lugar a una fracción equivalente. Si bien los números en la nueva fracción serán distintos, las fracciones poseerán el mismo valor.
- Por ejemplo, si tomamos la fracción 4/8 y multiplicamos tanto el numerador como el denominador por 2, obtendremos (4×2)/(8×2) = 8/16. Estas dos fracciones son equivalentes.
- (4×2)/(8×2) es básicamente lo mismo que 4/8 × 2/2. Recuerda que al multiplicar dos fracciones, lo hacemos de frente, lo que significa numerador por numerador y denominador por denominador.
- Ten en cuenta que 2/2 es igual a 1 cuando realices la división. Por lo tanto, es fácil ver la razón por la que 4/8 y 8/16 son equivalentes, ya que multiplicar 4/8 × (2/2) sigue siendo 4/8. De la misma manera es válido decir que 4/8 = 8/16.
- Cualquier fracción determinada tiene un número infinito de fracciones equivalentes. Puedes multiplicar el numerador y el denominador por cualquier entero sin importar lo grande o lo pequeña que sea la fracción equivalente que obtengas.
2
Divide el numerador y el denominador entre el mismo número. Del mismo modo que con la multiplicación, también es posible usar la división para hallar una fracción nueva que sea equivalente a la fracción original. Solo divide el numerador y el denominador de una fracción entre el mismo número para obtener una fracción equivalente. Sin embargo, ten en cuenta una cosa en este proceso, la fracción resultante debe tener números enteros tanto en el numerador como en el denominador para tener validez.
- Por ejemplo, observemos nuevamente a la fracción 4/8. Si en lugar de multiplicar, dividimos tanto el numerador como el denominador por 2, obtendremos (4 ÷ 2)/(8 ÷ 2) = 2/4. 2 y 4 son números enteros, así que esta fracción equivalente es válida.
Anuncio

Método 2

Método 2 de 5:
Utilizar la multiplicación básica para determinar la equivalencia

1
Halla el número por el cual necesites multiplicar el denominador más pequeño para crear el denominador más grande. Muchos problemas relacionados a las fracciones involucran el hecho de determinar si dos fracciones son equivalentes. Al calcular este número, puedes empezar a colocar las fracciones en los mismos términos para determinar la equivalencia.
- Por ejemplo, toma nuevamente las fracciones 4/8 y 8/16. El denominador más pequeño es 8 y tendríamos que multiplicar dicho número por 2 para obtener el denominador más grande, el cual es 16. Por lo tanto, en este caso el número es 2.
- En el caso de números más difíciles, puedes dividir simplemente el denominador más grande por el más pequeño. En este caso, 16 dividido entre 8 sigue siendo 2.
- El número podría no ser siempre un entero. Por ejemplo, si los denominadores eran 2 y 7, entonces el número sería 3,5.
2
Multiplica el numerador y el denominador de la fracción expresada en los términos inferiores por el número del primer paso. Las dos fracciones que son diferentes pero equivalentes tienen, por definición, numeradores y denominadores que son múltiplos entre sí. En otras palabras, multiplicar el numerador y el denominador de una fracción por el mismo número dará como resultado una fracción equivalente. Si bien los números en esta fracción nueva serán diferentes, las fracciones tendrán el mismo valor.^{[1]
X
Fuente de investigación}
- Por ejemplo, si tomamos la fracción 4/8 del paso uno y multiplicamos tanto el numerador como el denominador por el número que decidimos anteriormente, 2, obtendremos (4×2)/(8×2) = 8/16. De esta manera, se demuestra que estas dos fracciones son equivalentes.
Anuncio

Método 3

Método 3 de 5:
Utilizar la división básica para determinar la equivalencia

1
Calcula cada fracción como un número decimal. Para fracciones simples que no tienen variables, simplemente puedes expresar cada una de ellas como un número decimal para determinar la equivalencia. Dado que cada fracción en realidad se trata de un problema de división, esta será la manera más sencilla para determinar la equivalencia.
- Por ejemplo, tomemos la fracción utilizada anteriormente, 4/8. La fracción 4/8 es equivalente a 4 dividido entre 8, lo que significa que 4/8 = 0,5. También puedes resolver el otro ejemplo, que es 8/16 = 0,5. Independientemente de los términos de una fracción, dos números son equivalentes si son exactamente lo mismo cuando se expresan como decimal.
- Recuerda que la expresión decimal podría tener varios dígitos antes de que la falta de equivalencia se haga aparente. Como un ejemplo básico, 1/3 = 0,333 que se repite mientras que 3/10 = 0,3. Al utilizar más de un dígito, podemos ver que estas dos fracciones no son equivalentes.
2
Divide el numerador y el denominador de una fracción por el mismo número para obtener una fracción equivalente. En el caso de fracciones más complejas, el método de la división requiere de dos pasos adicionales. Al igual que con el método de la multiplicación, puedes dividir el numerador y el denominador de una fracción entre el mismo número para obtener una fracción equivalente. Sin embargo, existe algo que debes tener en cuenta en este proceso. Para ser válida, la fracción resultante debe tener números enteros tanto en el numerador como en el denominador.
- Por ejemplo, volvamos a la fracción 4/8. Si en lugar de multiplicar, dividimos el numerador y el denominador entre 2, obtendremos (4 ÷ 2)/(8 ÷ 2) = 2/4. 2 y 4 son números enteros, así que esta fracción equivalente es válida.
3
Reduce las fracciones hasta sus términos más bajos. Normalmente, la mayoría de las fracciones deben expresarse en sus términos más bajos y puedes convertirlas en sus términos más simples al dividirlas entre su máximo común divisor (MCD). Este paso funciona con la misma lógica de expresar fracciones equivalentes al convertirlas para tener el mismo denominador, pero este método busca reducir cada fracción a sus términos más bajos expresables.
- Si una fracción está en sus términos más simples, su numerador y denominador son los más pequeños posibles. Ninguno puede dividirse entre un número entero para obtener uno más pequeño. Para convertir una fracción que no está en sus términos más simples a una forma equivalente, dividiremos el numerador y el denominador entre su máximo común divisor.
- El máximo común divisor (MCD) del numerador y del denominador es el mayor número que divide a ambos para dar como resultado un número entero. De modo que en nuestro ejemplo con la fracción 4/8, dado que 4 es el mayor número que divide en partes iguales a 4 y 8, dividiremos tanto el numerador como el denominador de la fracción entre 4 para reducirla a sus términos más simples. (4 ÷ 4)/(8 ÷ 4) = 1/2. En el otro ejemplo con la fracción 8/16, el MCD es 8, que también da lugar a 1/2 como la expresión más simple de la fracción.
Anuncio

Método 4

Método 4 de 5:
Utilizar la regla de tres para hallar una variable

1
Iguala las dos fracciones. Utilizaremos la regla de tres para los problemas matemáticos donde sepamos que las fracciones son equivalentes, pero uno de los números ha sido reemplazado con una variable (por lo general, x) que debemos resolver. En casos como este, sabemos que estas fracciones son equivalentes porque son los únicos términos en los lados opuestos de un signo igual, pero a menudo la manera de hallar la variable no es evidente. Por suerte, con la regla de tres, resolver este tipo de problemas es sencillo.^{[2]
X
Fuente de investigación}
2
Toma las dos fracciones equivalentes y multiplica en forma de “x”. En otras palabras, multiplica el numerador de una fracción por el denominador de la otra y viceversa, luego iguala ambas respuestas y resuelve.^{[3]
X
Fuente de investigación}
- Toma los dos ejemplos con las fracciones 4/8 y 8/16. Estas dos fracciones no tienen una variable, pero podemos demostrar el concepto porque ya sabemos que son equivalentes. Al utilizar la regla de tres, sabemos que 4 x 16 = 8 x 8, o 64 = 64, lo que evidentemente es verdadero. Si ambos números no son iguales, entonces las fracciones no son equivalentes.
3
Introduce una variable. Dado que la regla de tres es el método más sencillo para determinar las fracciones equivalentes al resolver una variable, agreguemos una.
- Por ejemplo, consideremos la ecuación 2/x = 10/13. Para usar la regla de tres, multipliquemos 2 por 13 y 10 por “x”, luego igualamos las respuestas:
  - 2 × 13 = 26
  - 10 × x = 10x
  - 10x = 26. Desde aquí, obtener una respuesta para la variable es cuestión de álgebra simple. x = 26/10 = 2,6, lo que hace que las fracciones equivalentes iniciales sean 2/2,6 = 10/13.
4
Utiliza la regla de tres para las ecuaciones con múltiples variables o expresiones variables. Una de las mejores cosas que tiene la regla de tres es que funciona básicamente de la misma manera sin importar si lidias con dos fracciones simples (como las anteriores) o con unas más complejas. Por ejemplo, si ambas fracciones contienen variables, solo tienes que eliminar estas últimas al final durante el proceso de resolución. De manera similar, si los numeradores o los denominadores de las fracciones contienen expresiones variables (tales como x + 1), simplemente “multiplica a través” mediante la propiedad distributiva y resuelve como lo harías normalmente.^{[4]
X
Fuente de investigación}
- Por ejemplo, consideremos la siguiente ecuación ((x + 3)/2) = ((x + 1)/4). En este caso, al igual que en el anterior, resolveremos mediante la regla de tres:
  - (x + 3) × 4 = 4x + 12
  - (x + 1) × 2 = 2x + 2
  - 2x + 2 = 4x + 12, luego podemos simplificar la ecuación al restar 2x en ambos lados
  - 2 = 2x + 12, luego debemos aislar la variable al restar 12 en ambos lados
  - -10 = 2x y dividimos entre 2 para hallar x
  - -5 = x
Anuncio

Método 5

Método 5 de 5:
Utilizar la fórmula cuadrática para hallar las variables

1
Utiliza la regla de tres para multiplicar ambas fracciones. Para los problemas de equivalencia que requieran de la fórmula cuadrática, comenzamos utilizando la regla de tres. Sin embargo, cualquier tipo de multiplicación en x que involucre multiplicar términos con variables probablemente dará como resultado una expresión que no pueda resolverse con técnicas algebraicas. En casos como estos, es posible que necesites utilizar técnicas como la factorización o la fórmula cuadrática.^{[5]
X
Fuente de investigación}
- Por ejemplo, observemos la siguiente ecuación: ((x +1)/3) = (4/(2x - 2)). En primer lugar, utilicemos la regla de tres:
  - (x + 1) × (2x - 2) = 2x² + 2x -2x - 2 = 2x² - 2
  - 4 × 3 = 12
  - 2x² - 2 = 12.
2
Expresa la ecuación como si fuera una ecuación cuadrática. En este punto, deberemos expresar esta ecuación en forma cuadrática (ax² + bx + c = 0) al igualarla a 0. En este caso, restamos 12 en ambos lados para obtener 2x² - 14 = 0.
- Algunos valores podrían ser iguales a 0. Si bien 2x² - 14 = 0 es la forma más simple de nuestra ecuación, la verdadera ecuación cuadrática es 2x² + 0x + (-14) = 0. Probablemente ayudará a reflejar la forma de la ecuación cuadrática aun cuando algunos valores sean iguales a 0.
3
Resuelve al reemplazar los números de la ecuación cuadrática en la fórmula cuadrática. En este punto, la fórmula cuadrática (x = (-b +/- √(b² - 4ac))/2a) nos ayudará a hallar el valor de x.^{[6]
X
Fuente de investigación} No permitas que la extensión de la fórmula te intimide. Simplemente toma los valores de la ecuación cuadrática en el paso dos y reemplázalos en los lugares adecuados antes de resolver.
- x = (-b +/- √(b² - 4ac))/2a. En nuestra ecuación, 2x² - 14 = 0, a = 2, b = 0 y c = -14.
- x = (-0 +/- √(0² - 4(2)(-14)))/2(2)
- x = (+/- √( 0 - -112))/2(2)
- x = (+/- √(112))/2(2)
- x = (+/- 10.58/4)
- x = +/- 2,64
4
Verifica tu respuesta al reemplazar el valor de “x” en la ecuación cuadrática. Al reemplazar el valor calculado de “x” en la ecuación cuadrática del paso dos, puedes determinar fácilmente si obtuviste la respuesta correcta.^{[7]
X
Fuente de investigación} En este ejemplo, deberás reemplazar 2,64 y -2,64 en la ecuación cuadrática original.

Anuncio

Consejos

Convertir fracciones a sus formas equivalentes es realmente una forma de multiplicarlas por 1. Al convertir 1/2 a 2/4, multiplicar el numerador y el denominador por 2 es lo mismo que multiplicar 1/2 por 2/2, lo que da como resultado 1.
Si deseas, convierte los números mixtos a fracciones impropias para facilitar la conversión. Como es obvio, no todas las fracciones serán tan fáciles de convertir como las del ejemplo con 4/8. Por ejemplo, los números mixtos (p.ej. 1 3/4, 2 5/8, 5 2/3, etc.) pueden hacer que el proceso de conversión sea un poco más complicado. Si necesitas convertir un número mixto a una fracción equivalente, puedes hacerlo en dos formas: cambiar el número mixto a una fracción impropia y luego convertirlo como normalmente lo haces o mantenerlo y obtener un número mixto como respuesta.
- Para convertir a una fracción impropia, multiplica el número entero del número mixto por el denominador del componente fraccionario y luego súmalo al numerador. Por ejemplo, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Luego, si deseas, puedes realizar la conversión según sea necesario. Por ejemplo, 5/3 × 2/2 = 10/6, que sigue siendo equivalente a 1 2/3.
- Sin embargo, no es necesario convertir una fracción impropia como en el caso anterior. Si no lo hacemos, ignoramos el número entero, convertimos únicamente el componente fraccionario y luego sumamos el número entero sin alterarlo. Por ejemplo, en el caso de 3 4/16, solo nos enfocaremos en 4/16. 4/16 ÷ 4/4 = 1/4. Por lo tanto, sumar nuevamente el número entero nos dará como resultado un nuevo número mixto, 3 1/4.

Anuncio

Advertencias

Si bien al multiplicar fracciones multiplicas los numeradores y los denominadores, no sumes o restes estos últimos al realizar las operaciones de suma o resta.
- Por ejemplo, anteriormente descubrimos que 4/8 ÷ 4/4 = 1/2. Si en lugar de eso le sumáramos 4/4, obtendríamos un resultado completamente distinto. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 o 3/2, ninguno de los cuales es igual a 4/8.
La multiplicación y la división sirven para obtener fracciones equivalentes porque multiplicar y dividir formas fraccionarias del número 1 (2/2, 3/3, etc.) brinda respuestas que son equivalentes a la fracción original. La suma y la resta no permiten esta posibilidad.

Anuncio