Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 48 127 veces.
Los decimales periódicos, también conocidos como decimales recurrentes, son números decimales que tienen uno o más dígitos que se repiten indefinidamente en intervalos regulares. Trabajar con decimales periódicos a veces puede resultar confuso, pero puedes convertirlos en fracciones. Los decimales periódicos a veces se representan con una línea por encima de los dígitos que se repiten. El número 3,7777 donde se repite el 7, por ejemplo, también se puede escribir como 3,7. Para convertir un número como este en fracción debes escribirlo como ecuación, multiplicar, restar para quitarle la parte decimal que se repite y finalmente resolver la ecuación.
Pasos
Parte 1
Parte 1 de 2:Convertir decimales periódicos básicos
-
1Identifica el decimal que se repite. Por ejemplo, en el número 0,4444, el decimal que se repite es el 4. Es un decimal periódico básico en el sentido de que no hay una parte del número decimal que no se repita. Cuenta cuántos dígitos periódicos hay en el patrón.
- Una vez que escribas la ecuación, debes multiplicarla por 10y, donde y equivale a la cantidad de dígitos que se repiten en el patrón.[1]
- En el ejemplo de 0,4444 solo hay un dígito que se repite, por lo tanto, debes multiplicar la ecuación por 101.
- Si el decimal periódico es 0,4545, por ejemplo, entonces hay dos dígitos que se repiten. En ese caso deberás multiplicar la ecuación por 102.
- Si los dígitos que se repiten son tres, entonces deberás multiplicar por 103; y así sucesivamente.
-
2Reescribe el número decimal como ecuación. Escríbelo de modo tal que “x” sea igual al número original.[2] En este caso, la ecuación es x = 0,4444. Como solo hay un dígito decimal periódico, multiplica la ecuación por 101 (lo cual es igual a 10).
- En el ejemplo donde x = 0,4444, 10x = 4,4444.
- En el ejemplo donde x = 0,4545, hay dos dígitos que se repiten. Por lo tanto, deber multiplicar ambos lados de la ecuación por 102 (lo cual es igual a 100). Entonces: 100x = 45,4545.
-
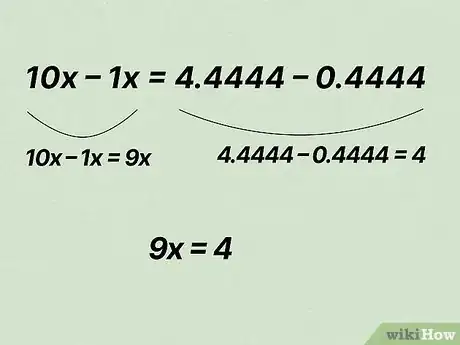
3Elimina los decimales periódicos. Para hacerlo, solo tienes que restarle x a 10x. Recuerda que todo lo que hagas en un lado de la ecuación debes hacerlo también en el otro. Por lo tanto:[3]
- 10x - 1x = 4,4444 - 0,4444
- En el lado izquierdo, tienes 10x - 1x = 9x. En el lado derecho, tienes 4,4444 - 0,4444 = 4.
- Por lo tanto, 9x = 4.
-
4Resuelve la ecuación para hallar el valor de x. Una vez que sabes a qué equivale 9x, puedes determinar el valor de “x” dividiendo entre 9 en ambos lados de la ecuación:
- En el lado izquierdo de la ecuación tienes 9x ÷ 9 = x. En el lado derecho de la ecuación tienes 4/9.
- Por lo tanto, x = 4/9 y el número decimal periódico 0,4444 se puede escribir como la fracción 4/9.
-
5Reduce la fracción. Expresa la fracción en su forma más simple (de ser necesario) dividiendo tanto el numerador como el denominador por el máximo común divisor entre ambos.
- En el ejemplo de 4/9, la fracción ya está expresada en su forma más simple.
Anuncio
Parte 2
Parte 2 de 2:Números periódicos con cifras no periódicas
-
1Identifica los dígitos periódicos. No es nada fuera de lo común encontrar números que tienen dígitos no periódicos antes de los decimales periódicos. Estos también se pueden convertir en fracciones.
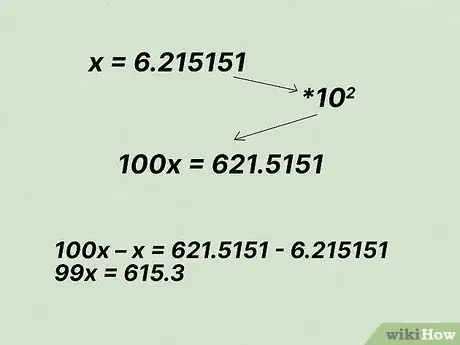
- Por ejemplo, toma el número 6,215151. En este caso, los dígitos no periódicos son el 6,2 y los dígitos periódicos son el 15.
- Una vez más, observa cuántos dígitos periódicos hay en el patrón ya que debes multiplicar por 10y tomando como base ese número.
- En este caso, hay dos dígitos periódicos, por lo que debes multiplicar la ecuación por 102.
-
2Escribe el problema como ecuación y resta los decimales periódicos. Una vez más, si x = 6,215151 entonces 100x = 621,5151. Para eliminar los decimales periódicos, réstalos en ambos lados de la ecuación:
- 100x - x (= 99x) = 621,5151 - 6,215151 (= 615,3)
- Por lo tanto, 99x = 615,3
-
3Resuelve la ecuación para hallar el valor de x. Como 99x = 615,3, divide ambos lados de la ecuación entre 99. Eso da como resultado x = 615,3/99.
-
4Elimina los decimales del numerador. Para hacerlo, multiplica el numerador y el denominador por 10z, donde z equivale a la cantidad de lugares decimales que debes desplazarte para eliminar el decimal. En 615,3 tienes que mover la coma solo un lugar, lo cual significa que tendrás que multiplicar el numerador y el denominador por 101:
- 615,3 x 10 / 99 x 10 = 6153/990
- Reduce la fracción dividiendo el numerador y el denominador entre el máximo común divisor, que en este caso es 3. De esta forma, el resultado final es x = 2051/330.
Anuncio






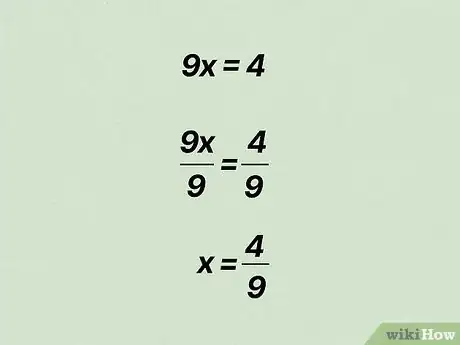























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 48 127 veces.