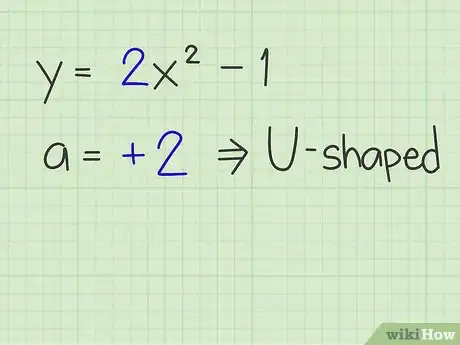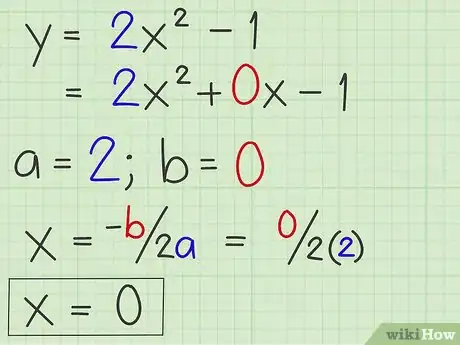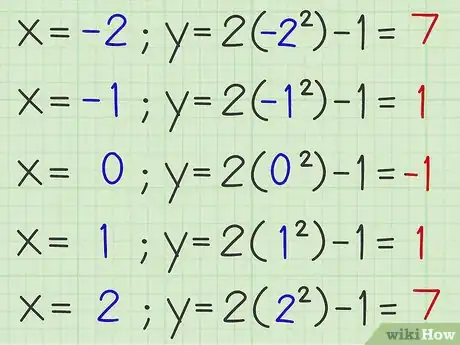Cómo dibujar una parábola

Coescrito por Jake Adams

Una parábola es una curva de dos dimensiones y de simetría especular que tiene forma de un arco. Cualquier punto de la parábola equidista de un punto fijo (el foco) y una línea recta fija (la directriz). Para poder dibujar un parábola, necesitas hallar su vértice así como varias coordenadas "x" e "y" en cualquier lado del vértice para marcar el camino que recorre. Si quieres saber cómo dibujar una parábola, empieza con el paso 1.

Parte 1

Parte 1 de 2:
Dibujando una parábola

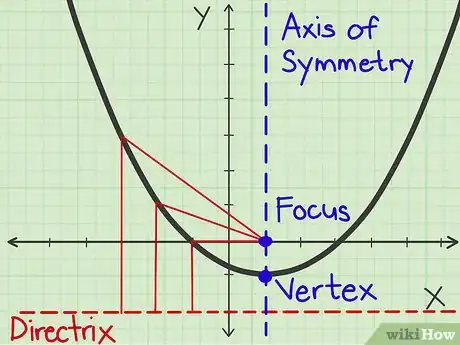
1
Aprende las partes de una parábola. Probablemente tengas determinada información antes de empezar y saber la terminología te ayudará a evitar cualquier proceso que no sea necesario. A continuación encontrarás las partes de la parábola que debes conocer:^{[1]
X
Fuente de investigación}
- El foco. Un punto fijo en el interior de la parábola que se usa para la definición formal de la curva.
- La directriz x. Una línea recta fija. La parábola es una curva en la que cualquier punto tiene la misma distancia desde el foco hasta la directriz.
- El eje de simetría. El eje de simetría es una línea vertical que atraviesa el punto de inflexión de la parábola. Cada lado del eje de simetría es una imagen especular.
- El vértice. El punto por el que el eje de simetría atraviesa la parábola se llama el vértice de la parábola. Si la parábola se abre hacia arriba, el vértice es un punto mínimo; si se abre hacia abajo, entonces el vértice es un punto máximo.
2
Conoce la ecuación de una parábola. La ecuación de una parábola es y = ax²+ bx + c. También se puede escribir de la siguiente manera: y = a(x – h)2 + k, pero este ejemplo se enfocará en la primera forma de la ecuación.
- Si la a en la ecuación es positiva, entonces la parábola se abre hacia arriba, como una "U" y tiene un punto mínimo. Si la a es negativa, entonces se abre hacia abajo y tiene un punto máximo. Si tienes problemas para recordarlo, piensa de esta forma: una ecuación con una a positiva luce como una sonrisa; una ecuación con una a negativa como un ceño.^{[2]
  X
  Fuente de investigación}
- Supongamos que tienes la siguiente ecuación: y = 2x² -1. Esta parábola tendrá la forma de una "U" porque el valor de a,2, es positivo.
- Si tu ecuación tuviera una coordenada y al cuadrado en lugar de una coordenada x al cuadrado, entonces se abriría hacia un lado, izquierdo o derecho, como una "C" o una "C" mirando hacia la izquierda. Por ejemplo, la parábola x² = y + 3 se abre hacia la derecha, como una "C".
3
Halla el eje de simetría. Recuerda que el eje de simetría es la línea vertical que atraviesa el punto de inflexión de la parábola. Es lo mismo que la coordenada x del vértice, que es el punto por el cual el eje de simetría atraviesa la parábola. Para hallar el eje de simetría utiliza esta fórmula: x = -b/2a^{[3]
X
Fuente de investigación}
- Al usar el ejemplo, se puede notar que a = 2, b = 0, y c=1. Ahora se puede calcular el eje de simetría al reemplazar los números: x = -0/(2 x 2) = 0.
- Tu eje de simetría es x = 0.
4
Halla el vértice. Cuando ya tengas tu eje de simetría, puedes reemplazar el valor de x para hallar la coordenada y. Estas dos coordenadas te darán el vértice de la parábola. En este caso, debes reemplazar 0 en 2x² -1 para hallar la coordenada y. y = 2 x 0² -1 = 0 -1 = -1. Tu vértice es (0,-1), que es el punto por el cual la parábola atraviesa el eje y. ^{[4]
X
Fuente de investigación}
- Los puntos del vértice también se conocen como los puntos (h, k). Tu punto h es 0 y tu punto k es -1. Si la ecuación de la parábola está en la forma y = a(x – h)2 + k, entonces tu vértice es simplemente el punto (h, k), y no necesitas hacer ningún cálculo para hallarlo más allá de interpretar correctamente el gráfico.
5
Establece una tabla con los valores de x. En este paso, debes crear una tabla donde coloques los valores de x en la primera columna. Esta tabla de otorgará las coordenadas que necesitas para dibujar tu parábola.
- El valor medio de x debe ser el eje de simetría.
- Debes incluir 2 valores por encima y por debajo del valor medio de x en la tabla, para que tenga simetría.
- En tu ejemplo, coloca el valor del eje de simetría, x = 0, en el centro de la tabla.
6
Calcula los valores de las coordenadas de y. Sustituye cada valor de x en la ecuación de la parábola y calcula los valores de y correspondientes. Incluye los valores calculados de y en la tabla. En tu ejemplo, la ecuación de la parábola se calcula de la siguiente manera:
- Para x = -2, y se calcula como: y = 2 x (-2)² - 1 = 8 - 1 = 7
- Para x = -1, y se calcula como: y = 2 x (-1)² - 1 = 2 - 1 = 1
- Para x = 0, y se calcula como: y = 2 x (0)² - 1 = 0 - 1 = -1
- Para x = 1, y se calcula como: y = 2 x (1)² - 1 = 2 - 1 = 1
- Para x = 2, y se calcula como: y = 2 x (2)² - 1 = 8 - 1 = 7
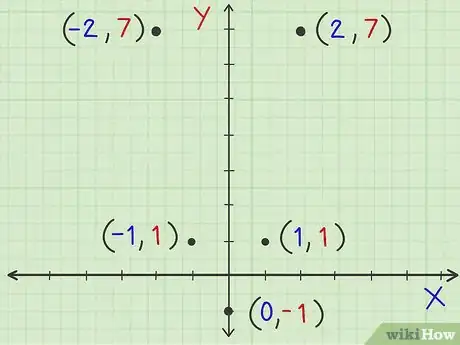
7
Incluye en la tabla los valores que se calcularon para y. Ahora que has hallado por lo menos 5 pares de coordenadas para la parábola, ya casi estás listo para dibujarla. Según tu trabajo, ahora tienes los siguientes puntos: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Ahora, pueden pensar que la parábola se refleja sobre el eje de simetría. Esto significa que las coordenadas de y que son reflejos directos de las otras a través del eje de simetría serán las mismas. Ambas coordenadas y para las coordenadas x, -2 y 2 son 7, ambas coordenadas y para las coordenadas x, -1 y 1, son 1, y así sucesivamente.
8
Dibuja los puntos de la tabla en el plano de coordenadas. Cada fila de la tabla forma una coordenada (x,y) en el plano de coordenadas. Dibuja todos los puntos con las coordenadas de la tabla en el plano de coordenadas.
- El eje x va de izquierda a derecha; el eje y va de arriba hacia abajo.
- Los números positivos en el eje y están sobre el punto (0, 0) y los números negativos en el eje y está debajo del punto (0, 0).
- Los números positivos del eje x están a la derecha del punto (0, 0) y los números negativos de eje x están a la derecha del punto (0, 0).
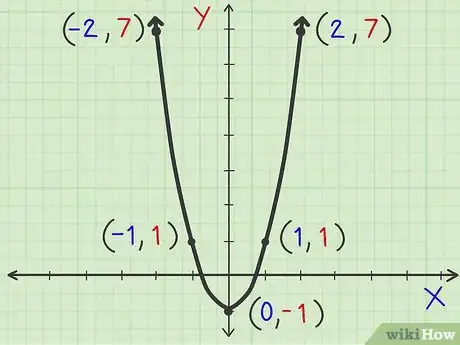
9
Une los puntos. Para dibujar la parábola, une los puntos del paso anterior. El gráfico de tu ejemplo se verá como una U. Asegúrate de unir los puntos usando una curva, en lugar de hacer que luzcan como segmentos. Esto creará la imagen más exacta de una parábola. También puedes dibujar flechas que señalen hacia arriba o hacia abajo en cada extremo de la parábola, dependiendo de su dirección. Esto indicará que el gráfico de la parábola continuará fuera del plano de coordenadas. ^{[5]
X
Fuente de investigación}

Parte 2

Parte 2 de 2:
Moviendo el gráfico de una parábola

Si quieres un atajo para mover una parábola sin tener que hallar su vértice y varios puntos, entonces puedes aprender a leer la ecuación de una parábola y aprender a moverla hacia arriba, abajo, a la derecha o a la izquierda. Empieza con la parábola básica y = x². Su vértice es (0, 0) y se abre hacia arriba. Algunos de sus puntos incluyen (-1, 1), (1, 1), (-2, 4), (2, 4), y así sucesivamente. Puedes aprender a mover la parábola según la ecuación con la que estás trabajando. ^{[6]
X
Fuente de investigación}

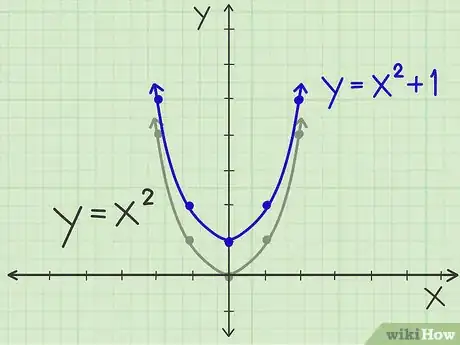
1
Mueve el gráfico de una parábola hacia arriba. Utiliza la ecuación y = x² +1. Todo lo que tienes que hacer es mover la parábola original 1 unidad hacia arriba, para que el vértice sea ahora (0, 1) en lugar de (0, 0). Aún tendrá la misma forma exacta de la parábola original, pero todas las coordenadas y se moverán 1 unidad hacia arriba. Así que en lugar de (-1, 1) y (1, 1), tienes (-1, 2) y (1, 2), y así sucesivamente.
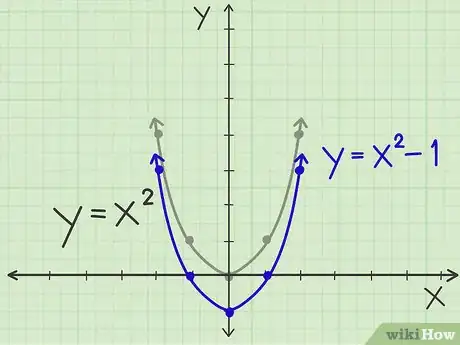
2
Mueve el gráfico de una parábola hacia abajo. Utiliza la ecuación y = x² -1. Todo lo que tienes que hacer es mover la parábola original 1 unidad hacia abajo, para que el vértice sea ahora (0, -1) en lugar de (0, 0). Aún tendrá la misma forma exacta de la parábola original, pero todas las coordenadas y se moverán 1 unidad hacia abajo. Así que en lugar de (-1, 1) y (1, 1), tienes (-1, 0) y (1, 0), y así sucesivamente.
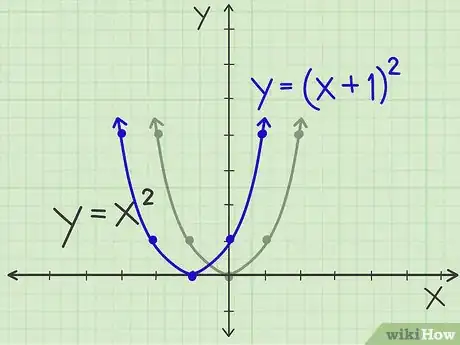
3
Mueve el gráfico de una parábola hacia la izquierda. Utiliza la ecuación y = (x + 1)². Todo lo que tienes que hacer es mover la parábola original 1 unidad hacia la izquierda, para que el vértice sea ahora (-1, 0) en lugar de (0, 0). Aún tendrá la misma forma exacta de la parábola original, pero todas las coordenadas x se moverán 1 unidad hacia la izquierda. Así que en lugar de (-1, 1) y (1, 1), tienes (-2, 1) y (0, 1), y así sucesivamente.
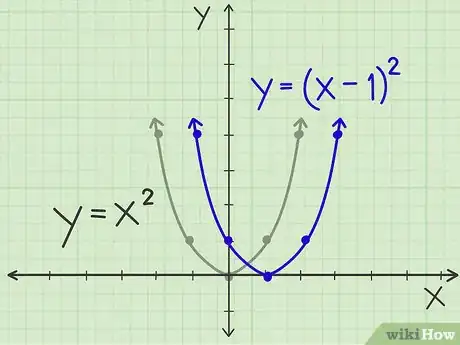
4
Mueve el gráfico de una parábola hacia la derecha. Utiliza la ecuación y = (x - 1)². Todo lo que tienes que hacer es mover la parábola original 1 unidad hacia la derecha, para que el vértice sea ahora (1, 0) en lugar de (0, 0). Aún tendrá la misma forma exacta de la parábola original, pero todas las coordenadas de x se moverán 1 unidad hacia la derecha. Así que en lugar de (-1, 1) y (1, 1), tienes (0, 1) y (2, 1), y así sucesivamente.